- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 数学記号の由来について(9)-数学定数(e、π、φ、i)-
コラム
2021年11月04日
文字サイズ
- 小
- 中
- 大
はじめに
何回かに分けて、これまで慣れ親しんできた数学で使用されている記号の由来について、報告している1。
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等、第6回は、無限大(∞)、比例(∝)、相似(∽)等、第7回は、三角関数(sin、cos、tan等)、第8回は「数」の記号について報告した。
今回は、数学定数についてということで、e(ネイピア数)、π(円周率)、黄金比φ、虚数単位iについて報告する。「数学定数」というのは、e(ネイピア数)、π(円周率)、黄金比φ、虚数単位i等のように、固定され、矛盾なく定義された定数のことを言い、数学の算式上に現われる定数a,b,c等とは異なるものであることを明確にするためにも「数学定数」と呼ばれている。
なお、e(ネイピア数)、π(円周率)、黄金比φに関する話題については、既に過去の研究員の眼で、それぞれ以下の通り何回かに分けて報告している。また、虚数iについても前回の研究員の眼「数学記号の由来について(8)-「数」を表す記号-」(2021.10.29)の中で報告している。従って、そちらも参考にしていただくことにして、今回はあくまでも記号の由来についてのみ述べることとする。
「ネイピア数eについて-ネイピア数とは何か、ネイピア数はどんな意味を有しているのか-」(2018.5.1)
「ネイピア数eについて(2)-ネイピア数は身近な数学的な問題の中でどのように現われてくる
のか-」(2018.5.8)
「ネイピア数eについて(3)-実際の社会における自然現象等の表現において、どのように現れ
てくるのか-」(2018.5.22)
「円周率πが現われる世界-ビュフォンの針の問題-」(2017.10.30)
「円周率πが現われる世界(2)-互いに素となる確率-」(2017.11.6)
「円周率πが現われる世界(3)-πが角度180°ってどういう意味-」(2017.11.13)
「円周率πが現われる世界(4)-3月14日は円周率(π)の日-」(2017.11.20)
「黄金比φについて(その1)-黄金比とはどのようなものなのか-」(2020.11.10)
「黄金比φについて(その2)-黄金比はどこで使用され、どんな場面で現れているのか-」(2020.11.20)
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等、第6回は、無限大(∞)、比例(∝)、相似(∽)等、第7回は、三角関数(sin、cos、tan等)、第8回は「数」の記号について報告した。
今回は、数学定数についてということで、e(ネイピア数)、π(円周率)、黄金比φ、虚数単位iについて報告する。「数学定数」というのは、e(ネイピア数)、π(円周率)、黄金比φ、虚数単位i等のように、固定され、矛盾なく定義された定数のことを言い、数学の算式上に現われる定数a,b,c等とは異なるものであることを明確にするためにも「数学定数」と呼ばれている。
なお、e(ネイピア数)、π(円周率)、黄金比φに関する話題については、既に過去の研究員の眼で、それぞれ以下の通り何回かに分けて報告している。また、虚数iについても前回の研究員の眼「数学記号の由来について(8)-「数」を表す記号-」(2021.10.29)の中で報告している。従って、そちらも参考にしていただくことにして、今回はあくまでも記号の由来についてのみ述べることとする。
「ネイピア数eについて-ネイピア数とは何か、ネイピア数はどんな意味を有しているのか-」(2018.5.1)
「ネイピア数eについて(2)-ネイピア数は身近な数学的な問題の中でどのように現われてくる
のか-」(2018.5.8)
「ネイピア数eについて(3)-実際の社会における自然現象等の表現において、どのように現れ
てくるのか-」(2018.5.22)
「円周率πが現われる世界-ビュフォンの針の問題-」(2017.10.30)
「円周率πが現われる世界(2)-互いに素となる確率-」(2017.11.6)
「円周率πが現われる世界(3)-πが角度180°ってどういう意味-」(2017.11.13)
「円周率πが現われる世界(4)-3月14日は円周率(π)の日-」(2017.11.20)
「黄金比φについて(その1)-黄金比とはどのようなものなのか-」(2020.11.10)
「黄金比φについて(その2)-黄金比はどこで使用され、どんな場面で現れているのか-」(2020.11.20)
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
「e」(ネイピア数)の由来
「ネイピア数(Napier’s constant)」は、通常「e」という記号で表される、次の定数である。
e = 2.71828182845904523536……
これは、無理数であり、「超越数2」と呼ばれているものである。
「ネイピア数」と呼ばれる理由については、現在ネイピア数と呼ばれているものについて、最も古くに研究を行ったジョン・ネイピア(John Napier:1550~1617)3に由来している。ただし、ジョン・ネイピア自体は、現在良く知られているようなネイピア数を示していたわけではなく、欧米ではむしろ、レオンハルト・オイラー(Leonhard Euler:1707~1783)に因んで、「オイラー数(Euler Number)」と呼ばれることもある4。
米国の数学者であり、数学史家のフロリアン・カジョリ(Florian Cajori)によれば、この定数に初めて定数記号を割り当てたのはドイツの数学者ゴットフリート・ライプニッツ(Gottfried Leibniz)で、1690年と1691年にオランダの数学者クリスティアーン・ホイヘンス(Christiaan Huygens )に宛てた手紙の中で、「b」という文字を使用した。その後、オイラーが1727年から1728年に書いた写本で、「e」という文字を使用した。
オイラーが「e」を使用した理由についての一般的なコンセンサスはないようで、Euler自身は非常に控えめな人間だったので、
「(1)自らの名前{Euler}の頭文字の「e」を採用したという説」
はあまり受け入れられていないようである。むしろ、以前の研究員の眼で説明したような定義から
「(2)「指数(exponential)」に由来しているとの説」や
「(3)文字のa、b、c、dが既に数学の他の場所で頻繁に使用されていたため、アルファベットの最初の「未使用」文字として選択されたという説」
「(4)eがaに続く母音であったことが関係していたという説」
があるようである。さらには、
「(5)「ein(ドイツ語の「1つ」の意味)」や「Einheit(ドイツ語の「単位」の意味)」の頭文字に由来しているとの説」
もあるようである。
いずれにしても、その後多くの数学者がこの「e」を使用することで、オイラーによって使用された他の多くの記号と同様に、普遍的に受け入れられて広く定着していったようである。
2 「超越数(transcendental number)」とは、有理数を係数にもついかなる代数方程式の解とはなりえない数(すなわち、どんな有理数 a0,a1,…,an を係数とする n 次の代数方程式 a0xn+a1xn-1+…+an-1x+an=0 の解にもならないような数)のことである。有理数は一次方程式の解であるから、超越的な実数はすべて無理数になるが、無理数 √2 は x2 − 2 = 0 の解であるから、逆は成り立たない。複素数(実数を含む)の中で,超越数でないものを「代数的数(algebraic number)」というが、代理的数は可算個しかなく,この意味で,複素数の大部分は超越数である。
3 ジョン・ネイピアは、スコットランドのバロンで、数学者、物理学者、天文学者、占星術師としても知られていた。「対数」の発見者とも言われている。
4 「オイラーの定数(Euler's constant)」あるいは「オイラー・マスケローニ定数(Euler–Mascheroni constant)」と一般的に呼ばれるものは、「γ(ガンマ)」で表される約0.5772156649 となる数である。
e = 2.71828182845904523536……
これは、無理数であり、「超越数2」と呼ばれているものである。
「ネイピア数」と呼ばれる理由については、現在ネイピア数と呼ばれているものについて、最も古くに研究を行ったジョン・ネイピア(John Napier:1550~1617)3に由来している。ただし、ジョン・ネイピア自体は、現在良く知られているようなネイピア数を示していたわけではなく、欧米ではむしろ、レオンハルト・オイラー(Leonhard Euler:1707~1783)に因んで、「オイラー数(Euler Number)」と呼ばれることもある4。
米国の数学者であり、数学史家のフロリアン・カジョリ(Florian Cajori)によれば、この定数に初めて定数記号を割り当てたのはドイツの数学者ゴットフリート・ライプニッツ(Gottfried Leibniz)で、1690年と1691年にオランダの数学者クリスティアーン・ホイヘンス(Christiaan Huygens )に宛てた手紙の中で、「b」という文字を使用した。その後、オイラーが1727年から1728年に書いた写本で、「e」という文字を使用した。
オイラーが「e」を使用した理由についての一般的なコンセンサスはないようで、Euler自身は非常に控えめな人間だったので、
「(1)自らの名前{Euler}の頭文字の「e」を採用したという説」
はあまり受け入れられていないようである。むしろ、以前の研究員の眼で説明したような定義から
「(2)「指数(exponential)」に由来しているとの説」や
「(3)文字のa、b、c、dが既に数学の他の場所で頻繁に使用されていたため、アルファベットの最初の「未使用」文字として選択されたという説」
「(4)eがaに続く母音であったことが関係していたという説」
があるようである。さらには、
「(5)「ein(ドイツ語の「1つ」の意味)」や「Einheit(ドイツ語の「単位」の意味)」の頭文字に由来しているとの説」
もあるようである。
いずれにしても、その後多くの数学者がこの「e」を使用することで、オイラーによって使用された他の多くの記号と同様に、普遍的に受け入れられて広く定着していったようである。
2 「超越数(transcendental number)」とは、有理数を係数にもついかなる代数方程式の解とはなりえない数(すなわち、どんな有理数 a0,a1,…,an を係数とする n 次の代数方程式 a0xn+a1xn-1+…+an-1x+an=0 の解にもならないような数)のことである。有理数は一次方程式の解であるから、超越的な実数はすべて無理数になるが、無理数 √2 は x2 − 2 = 0 の解であるから、逆は成り立たない。複素数(実数を含む)の中で,超越数でないものを「代数的数(algebraic number)」というが、代理的数は可算個しかなく,この意味で,複素数の大部分は超越数である。
3 ジョン・ネイピアは、スコットランドのバロンで、数学者、物理学者、天文学者、占星術師としても知られていた。「対数」の発見者とも言われている。
4 「オイラーの定数(Euler's constant)」あるいは「オイラー・マスケローニ定数(Euler–Mascheroni constant)」と一般的に呼ばれるものは、「γ(ガンマ)」で表される約0.5772156649 となる数である。
「π」(円周率)の由来
「π」は「円周率」を表しているが、これはギリシア語で周囲を表す「περίμετρος(= perimeter)」に由来している。
直径に対する円周の比率を表すために「π」を使用したのは、英国の数学者であるウィリアム・ジョーンズ(William Jones)で1706年に「Synopsis palmariorum mathesios」においてだったとされている。それ以前は2つの値の比として示されていた。例えば、これまで何度か出てきた英国の数学者ウィリアム・オートレッド(William Oughtred)は、1652 年において、π/δ(π は円周のギリシア語の頭文字、δ は直径(diameter)のギリシア語の頭文字)を使用していた。また、「ド・モアブルの定理」で有名なフランス生まれの英国の数学者アブラーム・ド・モアブル(Abraham de Moivre)は、円周率を「c/d」(円周(circle又はcircumference)/直径(diameter)あるいは「c/r」(radius)で表していたようである。
オイラーは一時「p」を使用したこともあったようだが、1737年に「π」を使用し、その後も「π」を使用するようになった。ヨハン・ベルヌーイ(Johann Bernoulli)が「e」を使用したりもしたが、「π」の使用が幅広く普及していったようである。
因みに、「π」の意味を日本語では「円周率」という比較的簡単な言葉で表現することができるが、これに対応する英語としては「the ratio of a circle's circumference to its diameter」というかなり長い言葉になってしまう。そのため、πの計算において貢献があった人物の名前から、「アルキメデス数」(Archimedes' constant)として呼ばれる。古代ギリシアの数学者アルキメデスは、幾何学的手法を用いて、円周率が小数点以下2位までの3.14の範囲にあることを示している。また、ドイツ語では円周率のことを「Kreiszahl」というが、一方で「ルドルフ数」(ドイツ語で Ludolphsche Zahl)とも呼ばれている。ルドルフ・ファン・コーレン(Ludolph van Ceulen)はドイツ生まれのオランダの数学者で、「π」を35桁目まで求めている。
直径に対する円周の比率を表すために「π」を使用したのは、英国の数学者であるウィリアム・ジョーンズ(William Jones)で1706年に「Synopsis palmariorum mathesios」においてだったとされている。それ以前は2つの値の比として示されていた。例えば、これまで何度か出てきた英国の数学者ウィリアム・オートレッド(William Oughtred)は、1652 年において、π/δ(π は円周のギリシア語の頭文字、δ は直径(diameter)のギリシア語の頭文字)を使用していた。また、「ド・モアブルの定理」で有名なフランス生まれの英国の数学者アブラーム・ド・モアブル(Abraham de Moivre)は、円周率を「c/d」(円周(circle又はcircumference)/直径(diameter)あるいは「c/r」(radius)で表していたようである。
オイラーは一時「p」を使用したこともあったようだが、1737年に「π」を使用し、その後も「π」を使用するようになった。ヨハン・ベルヌーイ(Johann Bernoulli)が「e」を使用したりもしたが、「π」の使用が幅広く普及していったようである。
因みに、「π」の意味を日本語では「円周率」という比較的簡単な言葉で表現することができるが、これに対応する英語としては「the ratio of a circle's circumference to its diameter」というかなり長い言葉になってしまう。そのため、πの計算において貢献があった人物の名前から、「アルキメデス数」(Archimedes' constant)として呼ばれる。古代ギリシアの数学者アルキメデスは、幾何学的手法を用いて、円周率が小数点以下2位までの3.14の範囲にあることを示している。また、ドイツ語では円周率のことを「Kreiszahl」というが、一方で「ルドルフ数」(ドイツ語で Ludolphsche Zahl)とも呼ばれている。ルドルフ・ファン・コーレン(Ludolph van Ceulen)はドイツ生まれのオランダの数学者で、「π」を35桁目まで求めている。
「φ」(黄金数)の由来
「φ(ファイ)」は「黄金数(golden number)」を表しており、具体的には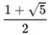 という数字のことをいう。この定数については、古代ギリシアの彫刻家ペイディアス(又はフェイディアス 、英語でPheidias、ギリシア語でΦειδίας)が初めて使ったと言われており、黄金数の記号「φ」は彼の頭文字に由来している。ペイディアスは、ギリシアのパルテノン神殿を建築した人物として有名で、実際にパルテノン神殿の中で黄金比が使用されていたようだ。
という数字のことをいう。この定数については、古代ギリシアの彫刻家ペイディアス(又はフェイディアス 、英語でPheidias、ギリシア語でΦειδίας)が初めて使ったと言われており、黄金数の記号「φ」は彼の頭文字に由来している。ペイディアスは、ギリシアのパルテノン神殿を建築した人物として有名で、実際にパルテノン神殿の中で黄金比が使用されていたようだ。
ただし、この記号が使われ始めたのは20世紀に入ってからであり、先のフロリアン・カジョリ(Florian Cajori)によれば、米国の数学者マーク・バー(Mark Barr)等は、(1)自らの彫刻で黄金比を頻繁に使用していたとされるPheidiasの名前の最初の文字であること、(2)πと絶えず取り組んでいる人々に馴染みのある音がしていること、から「φ」を提案し、採用したとされている。
なお、φではなくて、「τ(タウ)」を用いる場合もあるが、「τ」はギリシア語の「分割(section)」に由来している。英国の数学者ハロルド・スコット・マクドナルド・コクセター(Harold Scott MacDonald Coxeter)が1920年代から30年代に彼の論文で、さらに1948年の「Regular Polytopes」で使用している。
黄金比は、この黄金数を用いて、
 と表される。
と表される。
「黄金比」や「黄金数」の概念自体は、古代ギリシアの時代から存在しているが、この定数を記号で表すようになったのは、最近になってからということになる。
黄金数は、二次方程式 x2 − x − 1 = 0 の正の解であり、これが意味していることは、
幾何的には、a : b が黄金比ならば、
a:b = b : (a + b)
という等式が成り立つことから、縦横比が黄金比の矩形から最大正方形を切り落とした残りの矩形は、やはり黄金比の矩形となり、もとの矩形の相似になるという性質があることになる。
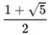 という数字のことをいう。この定数については、古代ギリシアの彫刻家ペイディアス(又はフェイディアス 、英語でPheidias、ギリシア語でΦειδίας)が初めて使ったと言われており、黄金数の記号「φ」は彼の頭文字に由来している。ペイディアスは、ギリシアのパルテノン神殿を建築した人物として有名で、実際にパルテノン神殿の中で黄金比が使用されていたようだ。
という数字のことをいう。この定数については、古代ギリシアの彫刻家ペイディアス(又はフェイディアス 、英語でPheidias、ギリシア語でΦειδίας)が初めて使ったと言われており、黄金数の記号「φ」は彼の頭文字に由来している。ペイディアスは、ギリシアのパルテノン神殿を建築した人物として有名で、実際にパルテノン神殿の中で黄金比が使用されていたようだ。ただし、この記号が使われ始めたのは20世紀に入ってからであり、先のフロリアン・カジョリ(Florian Cajori)によれば、米国の数学者マーク・バー(Mark Barr)等は、(1)自らの彫刻で黄金比を頻繁に使用していたとされるPheidiasの名前の最初の文字であること、(2)πと絶えず取り組んでいる人々に馴染みのある音がしていること、から「φ」を提案し、採用したとされている。
なお、φではなくて、「τ(タウ)」を用いる場合もあるが、「τ」はギリシア語の「分割(section)」に由来している。英国の数学者ハロルド・スコット・マクドナルド・コクセター(Harold Scott MacDonald Coxeter)が1920年代から30年代に彼の論文で、さらに1948年の「Regular Polytopes」で使用している。
黄金比は、この黄金数を用いて、
 と表される。
と表される。「黄金比」や「黄金数」の概念自体は、古代ギリシアの時代から存在しているが、この定数を記号で表すようになったのは、最近になってからということになる。
黄金数は、二次方程式 x2 − x − 1 = 0 の正の解であり、これが意味していることは、
幾何的には、a : b が黄金比ならば、
a:b = b : (a + b)
という等式が成り立つことから、縦横比が黄金比の矩形から最大正方形を切り落とした残りの矩形は、やはり黄金比の矩形となり、もとの矩形の相似になるという性質があることになる。
「i」(虚数単位)の由来
「i」は虚数単位とよばれるもので、二乗すると-1になる数を表している。則ち「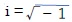 」あるいは「i2=-1」となる。この「i」という文字が最初に使用されたのは、フロリアン・カジョリ(Florian Cajori)によれば、レオンハルト・オイラー(Leonhard Euler)による、1777年に提示され、1794年に公表された論文においてであったようだ。
」あるいは「i2=-1」となる。この「i」という文字が最初に使用されたのは、フロリアン・カジョリ(Florian Cajori)によれば、レオンハルト・オイラー(Leonhard Euler)による、1777年に提示され、1794年に公表された論文においてであったようだ。
フランスの著名な哲学者・数学者であるルネ・デカルト(René Descartes)がその著書において、フランス語で「nombre imaginaire」(想像上の数)と名付けたことで、これが英語の「imaginary number」(虚数)の語源になった。
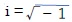 」あるいは「i2=-1」となる。この「i」という文字が最初に使用されたのは、フロリアン・カジョリ(Florian Cajori)によれば、レオンハルト・オイラー(Leonhard Euler)による、1777年に提示され、1794年に公表された論文においてであったようだ。
」あるいは「i2=-1」となる。この「i」という文字が最初に使用されたのは、フロリアン・カジョリ(Florian Cajori)によれば、レオンハルト・オイラー(Leonhard Euler)による、1777年に提示され、1794年に公表された論文においてであったようだ。フランスの著名な哲学者・数学者であるルネ・デカルト(René Descartes)がその著書において、フランス語で「nombre imaginaire」(想像上の数)と名付けたことで、これが英語の「imaginary number」(虚数)の語源になった。
最後に
今回は、e(ネイピア数)、π(円周率)、φ(黄金数)及びi(虚数単位)といった数学定数の記号の由来等について報告してきた。
日常何気なく使用している数学定数の記号であるが、その由来は、必ずしも明確でない部分もあるが、基本的にはそれらを表す用語やそれらを最初に使用した人の名の頭文字等に由来しているケースが多いようである。ただし、これらの記号についても、当初から明確に定められてきたというよりも、多くの人が使用することで定着してきた歴史を有しているようである。
日常何気なく使用している数学定数の記号であるが、その由来は、必ずしも明確でない部分もあるが、基本的にはそれらを表す用語やそれらを最初に使用した人の名の頭文字等に由来しているケースが多いようである。ただし、これらの記号についても、当初から明確に定められてきたというよりも、多くの人が使用することで定着してきた歴史を有しているようである。
本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2021年11月04日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【数学記号の由来について(9)-数学定数(e、π、φ、i)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数学記号の由来について(9)-数学定数(e、π、φ、i)-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




