- シンクタンクならニッセイ基礎研究所 >
- ネイピア数eについて-ネイピア数とは何か、ネイピア数はどんな意味を有しているのか-
コラム
2018年05月01日
文字サイズ
- 小
- 中
- 大
はじめに
皆さんは、「ネイピア数」と言われると、「それって何?」という感じだと思われる。「自然対数の底」だと言われると、そういえば、学生時代に対数を習った時に、確かにそんな概念を学んだ覚えがあるな、という方が多いのではないかと思われる。
今後、何回かに分けて、一般的に「e」という記号で表される「ネイピア数」が関係する話題について紹介したい。今回は、まずは「ネイピア数とは何か」について、説明する。
今後、何回かに分けて、一般的に「e」という記号で表される「ネイピア数」が関係する話題について紹介したい。今回は、まずは「ネイピア数とは何か」について、説明する。
ネイピア数とは
「ネイピア数(Napier’s constant)」とは、通常「e」という記号で表される、次の「数学定数1」と呼ばれる定数である。
e = 2.71828182845904523536……
これは、無理数であり、「超越数2」と呼ばれているものである。
因みに、円周率の「π」も超越数である。
では、なぜ「ネイピア数」と呼ばれるのか。それは、現在ネイピア数と呼ばれているものについて、最も古くに研究を行ったジョン・ネイピア(John Napier:1550~1617)3に由来している。ただし、ジョン・ネイピア自体は、現在良く知られているようなネイピア数を示していたわけではなかった。
その意味では、欧米ではむしろ、後に述べるレオンハルト・オイラー(Leonhard Euler:1707~1783)に因んで、「オイラー数(Euler Number)」と呼ばれることもある。
1 円周率のπや黄金比を表すφ等、固定され、矛盾なく定義された定数を、数学の算式上に現われる定数a,b,c等とは異な るものであることを明確にするためにも「数学定数」と呼んでいる。
2 超越数(transcendental number)とは、有理数を係数にもついかなる代数方程式の解とはなりえない数(すなわち、どんな有理数 a0,a1,…,an を係数とする n 次の代数方程式 a0xn+a1xn-1+…+an-1x+an=0 の解にもならないような数)のことである。有理数は一次方程式の解であるから、超越的な実数はすべて無理数になるが、無理数 √2 は x2 − 2 = 0 の解であるから、逆は成り立たない。複素数(実数を含む)の中で,超越数でないもの(代数的数)は可算個しかなく,この意味で,複素数の大部分は超越数である。
3 ジョン・ネイピアは、スコットランドのバロンで、数学者、物理学者、天文学者、占星術師としても知られていた。「対数」の発見者とも言われている。
e = 2.71828182845904523536……
これは、無理数であり、「超越数2」と呼ばれているものである。
因みに、円周率の「π」も超越数である。
では、なぜ「ネイピア数」と呼ばれるのか。それは、現在ネイピア数と呼ばれているものについて、最も古くに研究を行ったジョン・ネイピア(John Napier:1550~1617)3に由来している。ただし、ジョン・ネイピア自体は、現在良く知られているようなネイピア数を示していたわけではなかった。
その意味では、欧米ではむしろ、後に述べるレオンハルト・オイラー(Leonhard Euler:1707~1783)に因んで、「オイラー数(Euler Number)」と呼ばれることもある。
1 円周率のπや黄金比を表すφ等、固定され、矛盾なく定義された定数を、数学の算式上に現われる定数a,b,c等とは異な るものであることを明確にするためにも「数学定数」と呼んでいる。
2 超越数(transcendental number)とは、有理数を係数にもついかなる代数方程式の解とはなりえない数(すなわち、どんな有理数 a0,a1,…,an を係数とする n 次の代数方程式 a0xn+a1xn-1+…+an-1x+an=0 の解にもならないような数)のことである。有理数は一次方程式の解であるから、超越的な実数はすべて無理数になるが、無理数 √2 は x2 − 2 = 0 の解であるから、逆は成り立たない。複素数(実数を含む)の中で,超越数でないもの(代数的数)は可算個しかなく,この意味で,複素数の大部分は超越数である。
3 ジョン・ネイピアは、スコットランドのバロンで、数学者、物理学者、天文学者、占星術師としても知られていた。「対数」の発見者とも言われている。
ネイピア数は何を意味しているのか(その1)
ここで、n を限りなく大きくしていった場合の極限値がe(ネイピア数)ということになる。
n=1 の時は、 1+1=2
n=2 の時は、 (1+1/2)2=2.25
n=3 の時は、 (1+1/3)3=2.37037
n=4 の時は、 (1+1/4)4=2.441406
n=12 の時は、 (1+1/12)12=2.613035 月利
n=365 の時は、 (1+1/365)365=2.714567 日歩
というような具合で、n が大きくなっていくと、いつまでも値が大きくなっていくような印象を受けるかもしれない。実際には、「連続複利の元利合計」は無限に増大していくのではなく、e という値に収束していくことになる。
なお、年利が1ではなく、xである場合には、
n=1 の時は、 1+1=2
n=2 の時は、 (1+1/2)2=2.25
n=3 の時は、 (1+1/3)3=2.37037
n=4 の時は、 (1+1/4)4=2.441406
n=12 の時は、 (1+1/12)12=2.613035 月利
n=365 の時は、 (1+1/365)365=2.714567 日歩
というような具合で、n が大きくなっていくと、いつまでも値が大きくなっていくような印象を受けるかもしれない。実際には、「連続複利の元利合計」は無限に増大していくのではなく、e という値に収束していくことになる。
なお、年利が1ではなく、xである場合には、
となり、例えば、年利が1増加する毎に、元利合計額はe倍ずつ増加していくことになる。
ネイピア数は何を意味しているのか(その2)
となることから、結局は(その1)での定義と同じものとなることがわかる。
いずれにしても、この定義が意味するところは、ネイピア数は、「微分に対して指数関数を保存する数」であるということになる。ネイピア数のこの性質により、ネイピア数がいろいろな場面で使いやすい定数として用いられていくことになる。
いずれにしても、この定義が意味するところは、ネイピア数は、「微分に対して指数関数を保存する数」であるということになる。ネイピア数のこの性質により、ネイピア数がいろいろな場面で使いやすい定数として用いられていくことになる。
ネイピア数は何を意味しているのか(その3)
なぜ、「ネイピア数」は、「自然対数の底」と呼ばれるのか。
そもそも、「対数(logarithm)」とは何か。これについては、別途の機会に採り上げたいと思う。その中で「自然対数」とは何か、「底(てい)」って何か、と思われるのではないか。「自然対数」については、「eを底とする対数」4と定義されてしまうので、それでは「底」って何だ、ということになる。英語では「base」であり、即ち現在考えている対数の基礎となっているものである。具体的には、
指数関数y=ax で 対数関数 x=logay と表現される場合のaのこと あるいは
y=ax であるときに、x=logay と表現され、これを「aを底とするyの対数はxである」
ということになる。
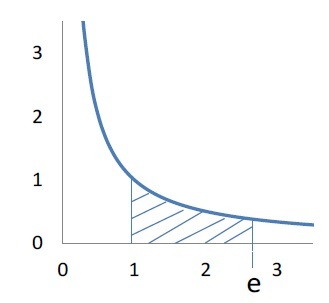
では、なぜこれが「自然」と名付けられるのかと言われると、これが数学の世界において、自然に現われてくるものであるということに由来している。具体的には、eを底とする対数については、(1)先に述べたようにその微分が 1/x となり、x = 1 における微分係数は 1 に等しくなることや、(2)単純な積分やテイラー級数で極めて容易に定義できることが、挙げられる。
4 因みに、10を底とする対数は「常用対数」と呼ばれている。
指数関数y=ax で 対数関数 x=logay と表現される場合のaのこと あるいは
y=ax であるときに、x=logay と表現され、これを「aを底とするyの対数はxである」
ということになる。
では、なぜこれが「自然」と名付けられるのかと言われると、これが数学の世界において、自然に現われてくるものであるということに由来している。具体的には、eを底とする対数については、(1)先に述べたようにその微分が 1/x となり、x = 1 における微分係数は 1 に等しくなることや、(2)単純な積分やテイラー級数で極めて容易に定義できることが、挙げられる。
4 因みに、10を底とする対数は「常用対数」と呼ばれている。
ネイピア数はどんなところで現れてくるのか
それでは、このネイピア数は、具体的に、我々の身近な数学的な問題の中でどのように現われてくるのか。さらには、実際の社会における自然現象や経済活動等の表現や分析の中で、どのように使用される形で現れてくるのか。これらについては、次回以降の研究員の眼で紹介していくこととしたい。
(2018年05月01日「研究員の眼」)
このレポートの関連カテゴリ
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【ネイピア数eについて-ネイピア数とは何か、ネイピア数はどんな意味を有しているのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
ネイピア数eについて-ネイピア数とは何か、ネイピア数はどんな意味を有しているのか-のレポート Topへ





















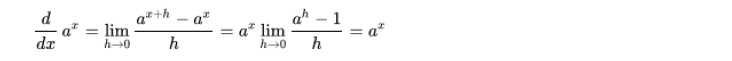





 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




