ネイピア数eについて（３）－実際の社会における自然現象等の表現において、どのように現れてくるのか

はじめに

前回の研究員の眼では「ネイピア数（Napier’s constant）」について、それが「我々の身近な数学的な問題の中でどのように現われてくるのか」について、紹介した。

今回は、この「ネイピア数」が「実際の社会における自然現象等の表現において、どのように現れてくるのか」について、紹介する。

ネイピア数eは、自然対数の底だと述べたが、文字通り自然対数の底として、自然界の各種の現象や人間の経済活動の表現に現われてくる。即ち、これらの現象や活動が指数関数的に変動（増加又は減少）していくことを表現する際に、ネイピア数が現われてくる。

ネイピア数が現れる世界（その１）－放射性物質の半減期－

まずは、最も有名でよく例に出されるのが、放射性物質の「半減期（half-life）」のケースである。

放射性物質に含まれる原子核は不安定で、放射線（α線、β線、γ線等）を放出して、他の元素に変化（放射性崩壊）していく。ある放射性物質の半分が放射性崩壊するまでの時間を「半減期」というが、この半減期は放射性物質の種類毎に一定の値となっている。

原子核数をNとし、tを時刻とすると

となる。ここに、λは崩壊定数と呼ばれるものである。

これにより、時刻tにおける原子核をN_t　とし、Nの初期値（t=0における値）をN₀とすると

　　N_t＝N₀e^－λ^t

となる。これから、半減期ｔについては

　　1／2＝e^－λ^t

となり

　　λt = log 2 （自然対数の2の値）＝　0.69314……

という関係が成立することになる。即ち、崩壊定数と半減期の積が（自然対数の2の値）log 2となる。

これにより、化石や火成岩等の放射性物質の減衰度合いを知ることで、その放射性物質の半減期から、その物質の年代推定を行うことができることになる。

ネイピア数が現れる世界（その２）－化学反応における物質濃度の半減期－

より一般的に、化学反応の速度が反応物質の濃度に比例する場合がある。いわゆる「１次反応」と言われるケースである。この場合、反応物は初期濃度から指数関数的に減少する。

反応物の濃度をAとし、tを時刻とすると

となる。ここに、kは反応速度定数と呼ばれるものである。

これにより、時刻tにおける濃度をAt　とし、Aの初期値（t=0における値）をA₀とすると、

　　A_t＝A₀e^－ｋ^t

ここでも、半減期をτとすると

　　kτ＝ log 2

という関係が成立する。即ち、反応速度定数と半減期の積がlog 2となる。

ネイピア数が現れる世界（その３）－お湯の冷却温度の変化－

より身近な例では、熱いお湯やコーヒー等の温度が冷める時の温度の変化は、指数関数を用いて表される。

「ニュートンの冷却の法則(Newton's law of cooling)」によれば、液体や気体等の媒質中に置かれた高温の固体が、周囲の媒質によって冷却される速度は、固体の表面積及び固体と媒質の温度差に比例する。即ち、固体の温度をT、媒質の温度をT_m、tを時刻とすると、以下の関係が成り立つ。

ここに、ｒは、固体の表面積、固体や媒質の性質等に依存する定数である。

これにより、時刻ｔにおける固体の温度Ttとし、Ｔの初期値（t=0における値）をＴ_０とすると

　　Ｔ_t＝Ｔ_ｍ＋（Ｔ_０－Ｔ_ｍ）e^－^rt

となる。

このように、温度は指数関数的に低下していくことになる。

ネイピア数が現れる世界（その４）－マルサスモデル－

生物の個体数や個体群サイズの増加や減少を記述する「マルサスモデル（Malthusian model）」は指数関数で表される数理モデルである。英国の経済学者トマス・ロバート・マルサスが、1798年に発表した『人口論』で、人口の増加について、この考え方を示したことに由来している。

ある生物の時刻ｔにおける個体数をP_tとし、Pの初期値（t=0における値）をP₀とすると、

　　P_t＝P₀ e^mt

と表される。ここに、mはマルサス係数と呼ばれるもので、mが正の時、Pは増加し、mが負の時、Pは減少していく。

ネイピア数が現れる世界（その５）－対数螺旋－

自然界に良く見られる螺旋の一種に「対数螺旋（logarithmic spiral）」¹と呼ばれるものがある。

いわゆる極座標表示（r, θ) を用いて

　　r＝ae^b^θ　　

と表される平面曲線である。ここに、e はネイピア数、a、b は実数である。

これを通常の直交座標表示（ｘ, ｙ)で表すと、以下の通りとなる。

　　ｘ＝ae^b^θcosθ　　ｙ＝　ae^b^θsinθ

rは原点からの距離を表す。

aは正値でスケールファクターとなっている。

bが螺旋の形状に大きな影響を与え、中心から離れる際に
(1) bが正値の場合は、左曲がりの螺旋になり、
(2) bが負値の場合は、右曲がりの螺旋になる。

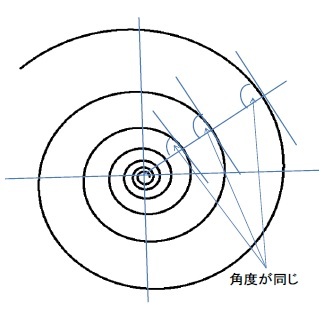歴史的な経緯から「対数螺旋」と呼ばれているが、実際の算式や図等から受ける感覚は「指数螺旋」に近いといえるかもしれない。

自然界で見られる対数螺旋の例としては、カタツムリ、オウムガイ、アンモナイトのような軟体動物の殻、牛や羊の角等で観察される。

さらには、台風（低気圧）の雲の形状にも観察される。

また、この「対数螺旋」が意味するところは、「この螺旋のどの点をとっても、その点と原点を結ぶ直線とその点における接線が交わる角度が一定になる」ということである。即ち、θが位置を表す角度を示しているが、交角がθによらない、ということになる。このため、対数螺旋は「等角螺旋（equiangular spiral）」とも呼ばれる。

この性質により、鳥や虫の飛行において、ある目標（例えば、獲物）に向かって飛んでくる場合に、常に一定の角度を保って、対数螺旋を描いてくる場合が観察されることになる。

なお、人工物の中にも対数螺旋は見られ、レオナルド・ダ・ヴィンチが設計したバチカン美術館の二重螺旋階段は、真上から見ると対数螺旋である、と言われている。

また、対数螺旋がある意味で「自然」であることを実感できる１つの身近な応用例として、対数螺旋の等角性を利用した最新型のハサミがある。これは、従来のハサミとは異なり、刃の内側を直線ではなく曲線（ベルヌーイカーブ刃と称している）にしている。これによって、刃元から刃先まで、切断が進んでいった場合にも、２つの刃の作り出す角度が、常に一定に保たれることになるため、切れやすいものとなっている。

¹ 後述するその螺旋の性質から「等角螺旋（equiangular spiral）」とも、また、その研究に貢献したスイスの数学者の名前から「ベルヌーイの螺旋（Bernoulli's spiral）」とも呼ばれる。

要するに

結局、これまでの例が意味するところは、「ある量 y の変化率が y 自身に比例するとき，y は指数関数で表される」ということである。これは、次のようにして示される。

変化率を表す比例定数を k として、 0 から x までの区間を等間隔の n 個の微小区間に分ける。各微小区間の右端における y の値はその左端における値の（1 + kx/n）倍になるので、yの初期値（y=0における値）をy₀とすると

　　y = y₀ (1 + kx/n)ⁿ

となる。ここで、n → ∞ とすると

　　y = y₀ e^kx

となる。

これは、まさにこのネイピア数に関する研究員の眼の第1回目で、ネイピア数eの最初の定義が示していたことである。

あるいは、微分を使用すれば

と表現されることから、これから、これまでの例と同様に、上記算式が得られることになる。

なお、任意の正数aに対して、a = e^logaであるから、eの代わりに任意の正数aを基準となる底として使うこともできるが、eが底として一番自然であることは、eが微分を保存する定数であること等、同じく以前の研究員の眼で説明したとおりである。

まとめ

今回は、ネイピア数が、実際の社会における自然現象や経済活動等の表現や分析において、どのように現れてくるのか、についてのいくつかの例を紹介した。

もちろん、ネイピア数は、ここで挙げた以上の数多くの事象を表現するために使用されているが、ここでの例からだけでも、ネイピア数が極めて「自然」に現われてくる定数であることが理解できるのではないかと思われる。

これまでの3回の研究員の眼を通じて、多くの人にとっては、学生時代に学んで、その後あまり接する機会がなかったと思われる「ネイピア数e」についての話題を紹介してきた。

これにより、少しは「ネイピア数」なるものに、興味・関心を抱いていただければと思っている。

ネイピア数eについて（３）－実際の社会における自然現象等の表現において、どのように現れてくるのか－ | ニッセイ基礎研究所

ネイピア数eについて（３）－実際の社会における自然現象等の表現において、どのように現れてくるのか－