- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 黄金比φについて(その2)-黄金比はどこで使用され、どんな場面で現れているのか-
コラム
2020年11月20日
文字サイズ
- 小
- 中
- 大
はじめに
「黄金比」について、前回の研究員の眼では、その定義及び関連した概念や歴史等について説明した。今回は、その「黄金比」が、どのようなところで使用され、どんな場面に現れているのかについて報告する。
黄金比の使用
黄金比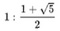 (その近似値は「1:1.618」)については、「長方形の縦横比が黄金比になると、安定した美感を与える」とか、「調和の取れた美しさがある」と言われている。図形や物体に対する感覚は人それぞれであるので、こうした言い方に対しては否定的な意見もあるかもしれない。
(その近似値は「1:1.618」)については、「長方形の縦横比が黄金比になると、安定した美感を与える」とか、「調和の取れた美しさがある」と言われている。図形や物体に対する感覚は人それぞれであるので、こうした言い方に対しては否定的な意見もあるかもしれない。
図形を考えた場合には、正方形が良いという人もいるかもしれないが、長方形では縦長よりも横長の方が安定感を感じるというのはその通りだろう。その中でどのような縦横比が最も心地よいと感じるのかは、どのような状況で使用されているのかにもよるだろう。
ただし、黄金比については、以下に述べるように自然界にも数多く存在していることから、人間が無意識に慣れ親しんだものとして、愛着や共感を覚えたりするものであるといえるのかもしれない。
いずれにしても、歴史的には黄金比(に近い比率)は、建築や芸術を初めとして、いろいろな場面で使用されてきたようだ。さらには、現代においても、各種のデザイン、建築、芸術作品等において、黄金比を取り入れたものが幅広く作成されてきており、黄金比の使用は1つの代表的なスキルやテクニックと考えられているようだ。
以下で、後解釈での説明だとの批判的な意見等を受けているものも含めて、黄金比が使用されていると言われているいくつかの例を紹介する。
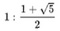 (その近似値は「1:1.618」)については、「長方形の縦横比が黄金比になると、安定した美感を与える」とか、「調和の取れた美しさがある」と言われている。図形や物体に対する感覚は人それぞれであるので、こうした言い方に対しては否定的な意見もあるかもしれない。
(その近似値は「1:1.618」)については、「長方形の縦横比が黄金比になると、安定した美感を与える」とか、「調和の取れた美しさがある」と言われている。図形や物体に対する感覚は人それぞれであるので、こうした言い方に対しては否定的な意見もあるかもしれない。図形を考えた場合には、正方形が良いという人もいるかもしれないが、長方形では縦長よりも横長の方が安定感を感じるというのはその通りだろう。その中でどのような縦横比が最も心地よいと感じるのかは、どのような状況で使用されているのかにもよるだろう。
ただし、黄金比については、以下に述べるように自然界にも数多く存在していることから、人間が無意識に慣れ親しんだものとして、愛着や共感を覚えたりするものであるといえるのかもしれない。
いずれにしても、歴史的には黄金比(に近い比率)は、建築や芸術を初めとして、いろいろな場面で使用されてきたようだ。さらには、現代においても、各種のデザイン、建築、芸術作品等において、黄金比を取り入れたものが幅広く作成されてきており、黄金比の使用は1つの代表的なスキルやテクニックと考えられているようだ。
以下で、後解釈での説明だとの批判的な意見等を受けているものも含めて、黄金比が使用されていると言われているいくつかの例を紹介する。
彫刻・絵画
古代ギリシアで制作された女性像「ミロのヴィーナス」は、その全身をへその部分で上下に分けたとき、下半身と上半身の比、あるいは全身と下半身の比が黄金比になっていると言われている。
イタリアの有名な画家であるレオナルド・ダ・ヴィンチもこの黄金比を発見して、彼の絵画の中で使用してきたと言われており、例えば、「モナリザ」の顔の横と縦の比が黄金比になっており、「最後の晩餐」の構図等において、いくつかの黄金比が使用されているようだ。さらには、映画「ダ・ヴィンチ・コード」でも取り上げられた有名なドローイングの「ウィトルウィウス的人体図」は理想的な人体比率を表したものになっているが、ここでも黄金比との関連が示唆されているようだ。
また、同じくルネッサンス期の有名な画家であるサンドロ・ボッティチェッリの「ヴィーナスの誕生」における女神の身体は黄金比に基づいて描かれているようだ。
さらに、ミケランジェロの「聖家族」は、前回説明した「五芒星(ごぼうせい)」の構図に基づいて描かれているようだ。
19世紀のフランスの画家ジャン=オーギュスト=ドミニク・アングル(Jean-Auguste-Dominique Ingres)は、その有名な絵画「泉」や「横たわるオダリスク」等で黄金比を使用しているようだ。
その後も黄金比を意識して創作した芸術家は多いと言われている。
なお、海外の美術作品だけでなく、例えば、葛飾北斎による「富嶽三十六景 神奈川沖浪裏」にも黄金比が使用されていると言われている。
イタリアの有名な画家であるレオナルド・ダ・ヴィンチもこの黄金比を発見して、彼の絵画の中で使用してきたと言われており、例えば、「モナリザ」の顔の横と縦の比が黄金比になっており、「最後の晩餐」の構図等において、いくつかの黄金比が使用されているようだ。さらには、映画「ダ・ヴィンチ・コード」でも取り上げられた有名なドローイングの「ウィトルウィウス的人体図」は理想的な人体比率を表したものになっているが、ここでも黄金比との関連が示唆されているようだ。
また、同じくルネッサンス期の有名な画家であるサンドロ・ボッティチェッリの「ヴィーナスの誕生」における女神の身体は黄金比に基づいて描かれているようだ。
さらに、ミケランジェロの「聖家族」は、前回説明した「五芒星(ごぼうせい)」の構図に基づいて描かれているようだ。
19世紀のフランスの画家ジャン=オーギュスト=ドミニク・アングル(Jean-Auguste-Dominique Ingres)は、その有名な絵画「泉」や「横たわるオダリスク」等で黄金比を使用しているようだ。
その後も黄金比を意識して創作した芸術家は多いと言われている。
なお、海外の美術作品だけでなく、例えば、葛飾北斎による「富嶽三十六景 神奈川沖浪裏」にも黄金比が使用されていると言われている。
建築
エジプトのピラミッドの高さと底辺の長さの比は黄金比になっていると言われている。
インドの有名なタージ・マハルは、アーチやファサード、ドーム等の部分に黄金比が使用されており、パリの凱旋門の中央開口部と全体の高さの比が1.697で黄金比に近いものとなっているようだ。さらに、パリのノートルダム大聖堂の薔薇窓においても黄金比が使用されているとのことである。また、建築家アントニ・ガウディの未完作品であるサグラダ・ファミリアや日本の唐招提寺金堂や金閣寺等も、その縦横比が黄金比になっているようである。
ニューヨークの国際連合ビル(Headquarters of the United Nations )は、横から見ると黄金比の長方形になっている。モダニズム建築の巨匠といわれ、世界遺産である東京・上野の国立西洋美術館の設計で有名なル・コルビュジエ(Le Corbusier)が黄金比を研究しており、国際連合ビルの設計委員会の主要メンバーだった。
ル・コルビュジエは、「モデュロール(Modulor)」と呼ばれる人体の寸法と黄金比から作った建造物の基準寸法の数列を開発し、これらを用いて数々の設計を行っている。Modulorは、フランス語のmodule(モジュール・寸法)とSection d'or(黄金分割)(あるいは黄金(or))から作られた造語である。
さらに、いわゆる建築物ではないのかもしれないが、京都の龍安寺の石庭は、黄金長方形で、大小15の石が5つの石組を構成しているが、これらは大小2つの黄金長方形の対角線の位置に配置されているとのことである。
インドの有名なタージ・マハルは、アーチやファサード、ドーム等の部分に黄金比が使用されており、パリの凱旋門の中央開口部と全体の高さの比が1.697で黄金比に近いものとなっているようだ。さらに、パリのノートルダム大聖堂の薔薇窓においても黄金比が使用されているとのことである。また、建築家アントニ・ガウディの未完作品であるサグラダ・ファミリアや日本の唐招提寺金堂や金閣寺等も、その縦横比が黄金比になっているようである。
ニューヨークの国際連合ビル(Headquarters of the United Nations )は、横から見ると黄金比の長方形になっている。モダニズム建築の巨匠といわれ、世界遺産である東京・上野の国立西洋美術館の設計で有名なル・コルビュジエ(Le Corbusier)が黄金比を研究しており、国際連合ビルの設計委員会の主要メンバーだった。
ル・コルビュジエは、「モデュロール(Modulor)」と呼ばれる人体の寸法と黄金比から作った建造物の基準寸法の数列を開発し、これらを用いて数々の設計を行っている。Modulorは、フランス語のmodule(モジュール・寸法)とSection d'or(黄金分割)(あるいは黄金(or))から作られた造語である。
さらに、いわゆる建築物ではないのかもしれないが、京都の龍安寺の石庭は、黄金長方形で、大小15の石が5つの石組を構成しているが、これらは大小2つの黄金長方形の対角線の位置に配置されているとのことである。
音楽
音楽の世界でも黄金比の使用が観測されるようだ。
名器中の名器と言われるバイオリンであるストラディバリウスの製作者であるアントニオ・ストラディバリも、楽器の全長を黄金比で分割した時に、その黄金比の来るところに、f字孔と呼ばれる穴の下の目の中心が来るように製作していた、と言われている。
また、フランスの有名な印象派の作曲家クロード・ドビュッシーの作品のいくつかは、黄金比を反映するセクションに分割することができ、フィボナッチ数列の連続する比率で近似できると言われている。さらに、ハンガリーの作曲家バルトーク・ベーラも小節数の設計等に、黄金比やフィボナッチ数列を使用して作曲していたと言われている。ただし、これらも作曲家自身が作曲時に意識的に黄金比を使用していたのか否かは定かではないようだ。
名器中の名器と言われるバイオリンであるストラディバリウスの製作者であるアントニオ・ストラディバリも、楽器の全長を黄金比で分割した時に、その黄金比の来るところに、f字孔と呼ばれる穴の下の目の中心が来るように製作していた、と言われている。
また、フランスの有名な印象派の作曲家クロード・ドビュッシーの作品のいくつかは、黄金比を反映するセクションに分割することができ、フィボナッチ数列の連続する比率で近似できると言われている。さらに、ハンガリーの作曲家バルトーク・ベーラも小節数の設計等に、黄金比やフィボナッチ数列を使用して作曲していたと言われている。ただし、これらも作曲家自身が作曲時に意識的に黄金比を使用していたのか否かは定かではないようだ。
会社のロゴ
Apple社の有名なロゴは、いくつかの曲線から形作られた林檎であるが、これはフィボナッチ数列の直径を有するいくつかの円から構成されていると言われている。ただし、このロゴのデザイナーであるロブ・ジャノフ氏が当初から意図的にこのような形で黄金比を使用していたのかは必ずしも明確ではないようだ。
また、Google社のロゴは、その直径の比が黄金比の大小2種類の円で構成されているようだ。
さらには、Zwitter社の青い小鳥のロゴも、いくつかの円の一部から成る曲線で構成されており、それらの円の大きさに黄金比が使用されているようだ。
加えて、Pepsi社のロゴは、黄金比によるいくつかの円に基づいているようだ。
また、Google社のロゴは、その直径の比が黄金比の大小2種類の円で構成されているようだ。
さらには、Zwitter社の青い小鳥のロゴも、いくつかの円の一部から成る曲線で構成されており、それらの円の大きさに黄金比が使用されているようだ。
加えて、Pepsi社のロゴは、黄金比によるいくつかの円に基づいているようだ。
日常生活で身近に見られるもの
名刺、カードのサイズ
身近なものでは、名刺等のカード類のサイズも黄金比を1つの基準とみなすことができるようなものになっている、名刺のサイズは国によっても統一されておらず、必ずしも黄金比に近いものにはなっていないケースもみられるようだが、日本における標準的な名刺のサイズは55×91mmでその縦横比は1.654となっている。また、標準的なクレジットカードやキャッシュカード、さらにはSuicaやICOCA等のサイズは53.98×85.60mmでその縦横比は1.585で黄金比に近くなっている。
本のサイズ
本のサイズはその種類によっても異なっている。新書本や漫画の単行本のサイズには、103×182mmと105×173mmがあり、後者の縦横比は1.647となり、黄金長方形に近くなっている。また、洋書で多いペーパーバックのサイズには、110×178mmのものがあり、この縦横比は1.618でまさに黄金比が使用される形になっている。
その他の使用例
たばこの箱のレギュラーサイズは、55×88mmでその縦横比は1.6となり、黄金比が使用された形になっている。
PC等の液晶ディスプレイのワイド画面のサイズは、従来10:16(縦横比は1.6)で、まさに黄金比が使用された形になっていたが、最近は液晶テレビと同様な9:16(=1.777)の比率が主流になってきており、黄金比に比べるとやや横長になってきている。
身近なものでは、名刺等のカード類のサイズも黄金比を1つの基準とみなすことができるようなものになっている、名刺のサイズは国によっても統一されておらず、必ずしも黄金比に近いものにはなっていないケースもみられるようだが、日本における標準的な名刺のサイズは55×91mmでその縦横比は1.654となっている。また、標準的なクレジットカードやキャッシュカード、さらにはSuicaやICOCA等のサイズは53.98×85.60mmでその縦横比は1.585で黄金比に近くなっている。
本のサイズ
本のサイズはその種類によっても異なっている。新書本や漫画の単行本のサイズには、103×182mmと105×173mmがあり、後者の縦横比は1.647となり、黄金長方形に近くなっている。また、洋書で多いペーパーバックのサイズには、110×178mmのものがあり、この縦横比は1.618でまさに黄金比が使用される形になっている。
その他の使用例
たばこの箱のレギュラーサイズは、55×88mmでその縦横比は1.6となり、黄金比が使用された形になっている。
PC等の液晶ディスプレイのワイド画面のサイズは、従来10:16(縦横比は1.6)で、まさに黄金比が使用された形になっていたが、最近は液晶テレビと同様な9:16(=1.777)の比率が主流になってきており、黄金比に比べるとやや横長になってきている。
自然界で見られる黄金比
黄金比は自然界でも見られるとされている。これは「フィボナッチ数列」と関係している要素が大きいので、詳しくは、次回以降の研究員の眼で「フィボナッチ数列」を紹介するときにも触れることとしたいが、ここでもいくつかの例を紹介しておく。
黄金螺旋
まずは、「黄金螺旋」について説明する。
下記の図が示すように、黄金長方形に正方形を加えていくと共に、四分円を描いていくと、外に拡がっていく渦巻き線をつくることができる。これは「黄金螺旋」と呼ばれている。「黄金螺旋」はより一般的な「対数螺旋」と呼ばれているものの一種であり、自然界では良く見られるものである。「対数螺旋」については、研究員の眼「ネイピア数eについて(3)-実際の社会における自然現象等の表現において、どのように現れてくるのか-」(2018.5.22)で報告したので。こちらを参照していただきたい。
まずは、「黄金螺旋」について説明する。
下記の図が示すように、黄金長方形に正方形を加えていくと共に、四分円を描いていくと、外に拡がっていく渦巻き線をつくることができる。これは「黄金螺旋」と呼ばれている。「黄金螺旋」はより一般的な「対数螺旋」と呼ばれているものの一種であり、自然界では良く見られるものである。「対数螺旋」については、研究員の眼「ネイピア数eについて(3)-実際の社会における自然現象等の表現において、どのように現れてくるのか-」(2018.5.22)で報告したので。こちらを参照していただきたい。
生物(の全体及びその一部(角、甲羅等))の成長を見ると、多くのケースにおいて相似形を保ちながら成長していくことが観測されるが、例えばこの黄金螺旋の形成状況を見れば、この際に空間を隙間なく充填していく様子が認識されることになる。
なお、「オウムガイの殻」の模様が黄金螺旋を描いている、と言われているが、これについては(対数螺旋ではあるものの)「螺旋に沿って中心から遠ざかる際に、中心からの直線距離がより速く大きくなる程度」を表すピッチ(pitch)が異なっており、必ずしも黄金螺旋ではないとの指摘もあるようである。
なお、「オウムガイの殻」の模様が黄金螺旋を描いている、と言われているが、これについては(対数螺旋ではあるものの)「螺旋に沿って中心から遠ざかる際に、中心からの直線距離がより速く大きくなる程度」を表すピッチ(pitch)が異なっており、必ずしも黄金螺旋ではないとの指摘もあるようである。
ひまわりの花
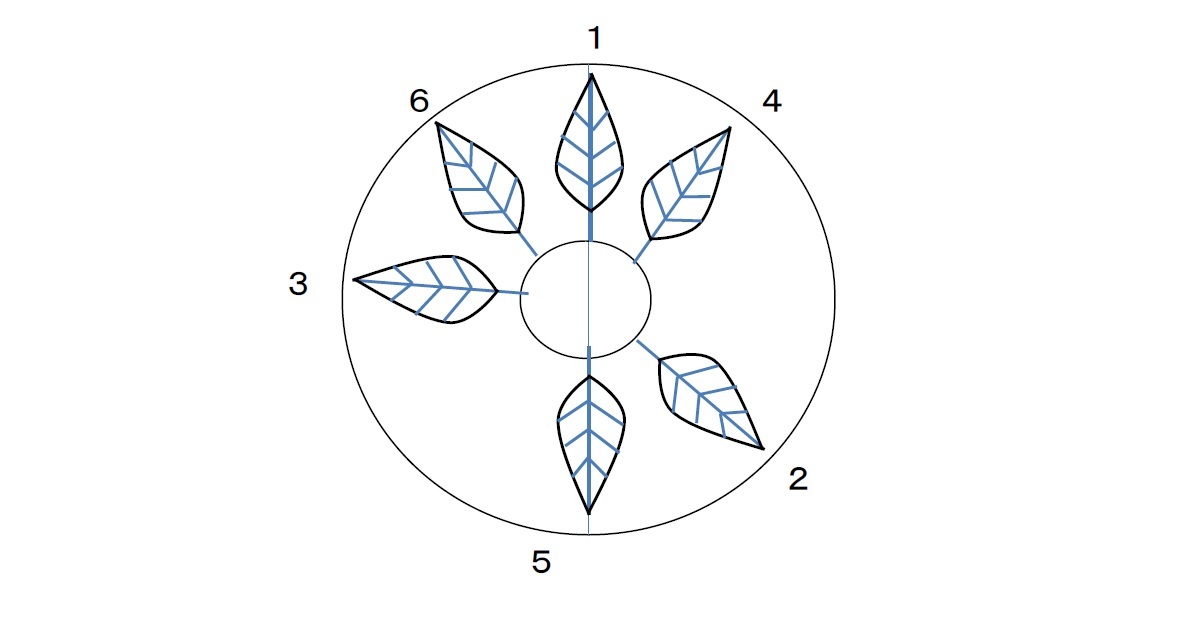
黄金比の話題になる時に、「ひまわりの花」がよく例に挙げられる。
ひまわりの花というのは、下記の写真でわかるように、外側に大きな花びらがあり、内側に小さな丸い粒のようなものが数多く見える形になっている。実は、この粒のようなものは小さな花(小花)となっており、これらの多数の小花が集まって1つの花のように見える構造となっている。ただし、それぞれの小花から種子ができるため、一般的にはこれらを指して種子と呼んでいることも多い。この中央から始まる小花(種子)の列が上記の黄金螺旋に相当していると言われている。
このひまわりの小花は、実は前回の研究員の眼で述べた「黄金角」(約137.5°)に従って、時計回りと反時計回りに配列された黄金螺旋で構成されており、それぞれの黄金螺旋の本数はフィボナッチ数(21と34、34と55等)になっているようだ。
こうすることで、円の内側に直線的に配列される場合に比べて、不要な空白の場所が節約できて、最も効率的に多くの小花を配列することができることになる。ただし、自然界でたびたび観測されるように、螺旋の数が多い場合には、中心から離れると螺旋の隙間にも種ができてしまい、途中から枝分かれしてフィボナッチ数にならないこともあるようだ。
黄金比の話題になる時に、「ひまわりの花」がよく例に挙げられる。
ひまわりの花というのは、下記の写真でわかるように、外側に大きな花びらがあり、内側に小さな丸い粒のようなものが数多く見える形になっている。実は、この粒のようなものは小さな花(小花)となっており、これらの多数の小花が集まって1つの花のように見える構造となっている。ただし、それぞれの小花から種子ができるため、一般的にはこれらを指して種子と呼んでいることも多い。この中央から始まる小花(種子)の列が上記の黄金螺旋に相当していると言われている。
このひまわりの小花は、実は前回の研究員の眼で述べた「黄金角」(約137.5°)に従って、時計回りと反時計回りに配列された黄金螺旋で構成されており、それぞれの黄金螺旋の本数はフィボナッチ数(21と34、34と55等)になっているようだ。
こうすることで、円の内側に直線的に配列される場合に比べて、不要な空白の場所が節約できて、最も効率的に多くの小花を配列することができることになる。ただし、自然界でたびたび観測されるように、螺旋の数が多い場合には、中心から離れると螺旋の隙間にも種ができてしまい、途中から枝分かれしてフィボナッチ数にならないこともあるようだ。
黄金分割探索
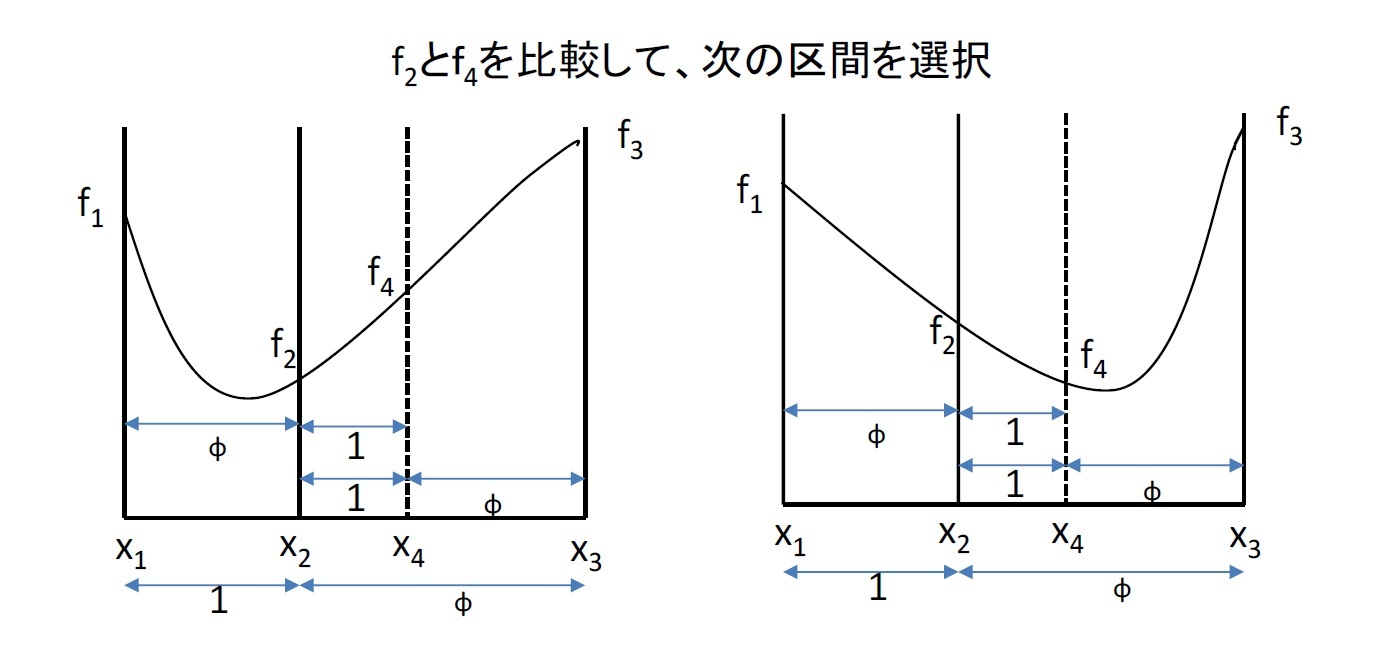
ここで、黄金比がより実用的にどのように役立っているのかを示す1つの例として「黄金分割探索」について紹介しておく。「黄金分割探索」は、いわゆる「単峰関数」と呼ばれる、まさに峰が1つの関数(例えば、2次関数等)の極値(いわゆる最大値や最小値)を効率的に求める方法1である。
具体的には、例えば、1本の管のいずれかの箇所に問題があり、その問題箇所を認知するための検査数値が単峰関数f(x)で表されることがわかっている場合、どのような手順を踏んだらよいのかという問題である。
この場合、まずは管を黄金比で内分する点で検査を行い、問題のある箇所の側を特定する。次にその問題がある側の管の黄金比で内分する点で検査を行う、ということを繰り返していくことで、問題の箇所を効率的に特定していくことができることになる。
黄金分割探索の概要を図で示すと、以下の通りとなる。
具体的には、例えば、1本の管のいずれかの箇所に問題があり、その問題箇所を認知するための検査数値が単峰関数f(x)で表されることがわかっている場合、どのような手順を踏んだらよいのかという問題である。
この場合、まずは管を黄金比で内分する点で検査を行い、問題のある箇所の側を特定する。次にその問題がある側の管の黄金比で内分する点で検査を行う、ということを繰り返していくことで、問題の箇所を効率的に特定していくことができることになる。
黄金分割探索の概要を図で示すと、以下の通りとなる。
1 黄金分割探索を整数のみで行う方法は「フィボナッチ探索」と言われている。
最後に
今回は、「黄金比」について、2回に分けて触れてきた。
このコラムを書いていて、つい先日セルフサービスのカフェで軽食を食べようとしたら、トレーがまさに見事にピッタリの黄金比になっていて、多少驚いた。このように、黄金比は日常生活の至る所で見つけることができる。
なお、今回の研究員の眼では、黄金比の記号の使用と由来については触れていない。これについては、現在連載している「数学記号の由来」シリーズで、後日報告することにしたい。また、「黄金比」とは別の「貴金属比」である「白銀比」等については、次回の研究員の眼で述べることにしたい。さらに、黄金比と関係しているとして何度か述べてきた「フィボナッチ数列」については、次回以降の研究員の眼で詳しく報告することにしたい。
このコラムを書いていて、つい先日セルフサービスのカフェで軽食を食べようとしたら、トレーがまさに見事にピッタリの黄金比になっていて、多少驚いた。このように、黄金比は日常生活の至る所で見つけることができる。
なお、今回の研究員の眼では、黄金比の記号の使用と由来については触れていない。これについては、現在連載している「数学記号の由来」シリーズで、後日報告することにしたい。また、「黄金比」とは別の「貴金属比」である「白銀比」等については、次回の研究員の眼で述べることにしたい。さらに、黄金比と関係しているとして何度か述べてきた「フィボナッチ数列」については、次回以降の研究員の眼で詳しく報告することにしたい。
本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2020年11月20日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月16日
EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- -
2025年10月16日
再び不安定化し始めた米中摩擦-経緯の振り返りと今後想定されるシナリオ -
2025年10月15日
インド消費者物価(25年10月)~9月のCPI上昇率は1.5%に低下、8年ぶりの低水準に -
2025年10月15日
「生活の質」と住宅価格の関係~教育サービス・治安・医療サービスが新築マンション価格に及ぼす影響~ -
2025年10月15日
IMF世界経済見通し-世界成長率見通しは3.2%まで上方修正
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【黄金比φについて(その2)-黄金比はどこで使用され、どんな場面で現れているのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
黄金比φについて(その2)-黄金比はどこで使用され、どんな場面で現れているのか-のレポート Topへ




















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




