- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「ハッピー数」や「幸運数」という名前の数字があるってこと知っていますか?
コラム
2020年04月03日
文字サイズ
- 小
- 中
- 大
はじめに
「ハッピー数」とは
「ハッピー数(happy number)」というのは、自然数の各桁を1桁毎に分解して、それぞれの二乗和を取り、新しくできた数についても同じ処理を繰り返すことによって、最終的に1となる数を指す。
このように説明すると、一体何だと思われる方も多いと思う。具体的に、「23」という数字を例に考えてみると、以下の通りとなる。
「23」を「2」と「3」に分解して、 22+32=13
「13」を「1」と「3」に分解して、 12+32=10
「10」を「1」と「0」に分解して、 12+02=1
これにより、「23」はハッピー数と言うことになる。
このように説明すると、一体何だと思われる方も多いと思う。具体的に、「23」という数字を例に考えてみると、以下の通りとなる。
「23」を「2」と「3」に分解して、 22+32=13
「13」を「1」と「3」に分解して、 12+32=10
「10」を「1」と「0」に分解して、 12+02=1
これにより、「23」はハッピー数と言うことになる。
「アンハッピー数」とは
「ハッピー数(happy number)」でない自然数は「アンハッピー数(unhappy number)」と呼ばれる。実は、全体の自然数の7分の1がハッピー数に、残りの7分の6がアンハッピー数に分類されることになる。
アンハッピー数の場合、自然数の各桁を1桁毎に分解して、それぞれの二乗和を取り、新しくできた数についても同じ処理を繰り返すことによって、最終的には4となる。
具体的には「12」は、以下の通りの結果から、アンハッピー数となる。
「12」を「1」と「2」に分解して、 12+22=5
52=25
「25」を「2」と「5」に分解して、 22+52=29
「29」を「2」と「9」に分解して、 22+92=85
「85」を「8」と「5」に分解して、 82+52=89
「89」を「8」と「9」に分解して、 82+92=145
「145」を「1」と「4」と「5」に分解して、 12+42+52=42
「42」を「4」と「2」に分解して、 42+22=20
「20」を「2」と「0」に分解して、 22+02=4
となる。実は「4」という数字に同じことを繰り返すと、
「4」→「16」→「37」→「58」→「89」→「145」→「42」→「20」→「4」
というプロセスで結局再び「4」に戻ってくる。
アンハッピー数の場合、自然数の各桁を1桁毎に分解して、それぞれの二乗和を取り、新しくできた数についても同じ処理を繰り返すことによって、最終的には4となる。
具体的には「12」は、以下の通りの結果から、アンハッピー数となる。
「12」を「1」と「2」に分解して、 12+22=5
52=25
「25」を「2」と「5」に分解して、 22+52=29
「29」を「2」と「9」に分解して、 22+92=85
「85」を「8」と「5」に分解して、 82+52=89
「89」を「8」と「9」に分解して、 82+92=145
「145」を「1」と「4」と「5」に分解して、 12+42+52=42
「42」を「4」と「2」に分解して、 42+22=20
「20」を「2」と「0」に分解して、 22+02=4
となる。実は「4」という数字に同じことを繰り返すと、
「4」→「16」→「37」→「58」→「89」→「145」→「42」→「20」→「4」
というプロセスで結局再び「4」に戻ってくる。
「ハッピー数」と「アンハッピー数」
「1」と「4」以外の一桁の自然数については、以下の通りとなる。
「2」→「4」
「3」→「9」→「81」→「65」→「61」→「37」→「58」→「89」→「145」→「42」→「20」→「4」
「5」→「25」→「29」→「85」→「89」→「145」→「42」→「20」→「4」
「6」→「36」→「45」→「41」→「17」→「50」→「25」→「29」→「85」→「89」→「145」→「42」→「20」→「4」
「7」→「49」→「97」→「130」→「10」→「1」
「8」→「64」→「52」→「29」→「85」→「89」→「145」→「42」→「20」→「4」
「9」→「81」→「65」→「61」→「37」→「58」→「89」→「145」→「42」→「20」→「4」
このようにして、一桁の自然数のうち、「1」と「7」はハッピー数であるが、それ以外が「アンハッピー数」ということになる。
因みに、100以下のハッピー数は、以下の通りとなっている。
1、7、10、13、19、23、28、31、32、44、49、68、70、79、82、86、91、94、97、100
「2」→「4」
「3」→「9」→「81」→「65」→「61」→「37」→「58」→「89」→「145」→「42」→「20」→「4」
「5」→「25」→「29」→「85」→「89」→「145」→「42」→「20」→「4」
「6」→「36」→「45」→「41」→「17」→「50」→「25」→「29」→「85」→「89」→「145」→「42」→「20」→「4」
「7」→「49」→「97」→「130」→「10」→「1」
「8」→「64」→「52」→「29」→「85」→「89」→「145」→「42」→「20」→「4」
「9」→「81」→「65」→「61」→「37」→「58」→「89」→「145」→「42」→「20」→「4」
このようにして、一桁の自然数のうち、「1」と「7」はハッピー数であるが、それ以外が「アンハッピー数」ということになる。
因みに、100以下のハッピー数は、以下の通りとなっている。
1、7、10、13、19、23、28、31、32、44、49、68、70、79、82、86、91、94、97、100
なぜ「ハッピー数」という名称が付与されたのか
実は、ハッピー数の考え方が初めて示されたのは、1970年代のロシアと考えられているようだが、この数の発見についての起源はあまりはっきりしていないようである。また、「ハッピー数(happy number)」という名称の数学的な理由も明確ではないようだ。
ただし、数字の「7」が西洋において、一般的に幸運な数字として認識されていることから、7がこの定義に合致して、7分の1の確率でハッピー数が存在する、という事実から、ある意味で自然なネーミングといえるのかもしれない。
また、「アンハッピー数」の名称は、もちろん「「ハッピー数」ではない数」という意味での名称ではあるが、それでもこのような言い方を日本語でされると、多くの方々はあまり良い印象を持たれないものと思われる。全ての数字がそれぞれに重要性を有した意味あるものであることは言うまでもないからである。
ただし、数字の「7」が西洋において、一般的に幸運な数字として認識されていることから、7がこの定義に合致して、7分の1の確率でハッピー数が存在する、という事実から、ある意味で自然なネーミングといえるのかもしれない。
また、「アンハッピー数」の名称は、もちろん「「ハッピー数」ではない数」という意味での名称ではあるが、それでもこのような言い方を日本語でされると、多くの方々はあまり良い印象を持たれないものと思われる。全ての数字がそれぞれに重要性を有した意味あるものであることは言うまでもないからである。
「ハッピー数」は無数存在する
その定義から、自明のことではあるが、ある数字がハッピー数なら、桁の順番を入れ替えた数もハッピー数となる。例えば「23」はハッピー数なので、「32」もハッピー数となる。また、途中に0を挿入した数もハッピー数となる。例えば「203」や「2030」などもハッピー数となる。
従って、ハッピー数は無数に存在することになる。
従って、ハッピー数は無数に存在することになる。
「幸運数」とは
ここで、4番目に得られる「9」は幸運数となる。
以下同様に無限にこの操作を続けていって、取り除く数を増やしていっても残る数が幸運数である。
以下同様に無限にこの操作を続けていって、取り除く数を増やしていっても残る数が幸運数である。
なぜ「幸運数」という名称が付与されたのか
「幸運数」という用語は、1956年にGardiner、Lazarus、Metropolis、Ulamの論文で紹介された。彼らが、「ジョセフス問題(Josephus problem)」のカウントアウト(除外)ゲームとの類似性から、その定義する篩を「ジョセフス・フラビウスの篩」と呼ぶことを提案したことに由来している。
「ジョセフス問題」というのは、以下のような問題である。
「n 人の人間が円を描くように並び、処刑されるのを待っている。最初の人をスキップし、さらに(k – 2)人をスキップし(つまり、(k – 1)人をスキップして k番目の人に到達する)、k番目の人を処刑する。そしてそこから、再度 (k – 1)人をスキップして k番目の人を処刑する。これを延々と続けていって、最後に残った1人を釈放する。」
この問題そのものはあまりハッピーなものではない。
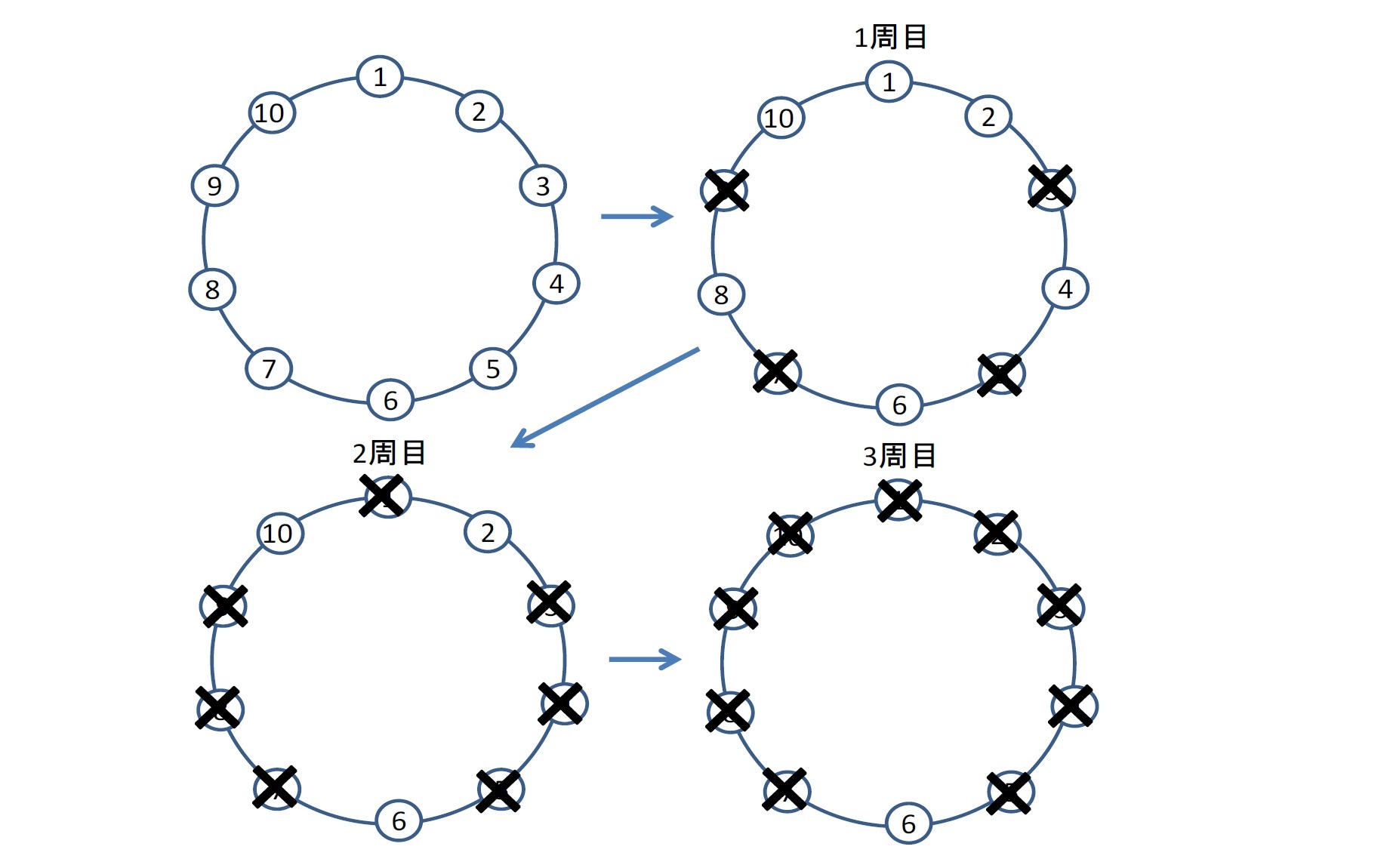
n=10 k=2 の場合については、以下の通りとなる。
「ジョセフス問題」というのは、以下のような問題である。
「n 人の人間が円を描くように並び、処刑されるのを待っている。最初の人をスキップし、さらに(k – 2)人をスキップし(つまり、(k – 1)人をスキップして k番目の人に到達する)、k番目の人を処刑する。そしてそこから、再度 (k – 1)人をスキップして k番目の人を処刑する。これを延々と続けていって、最後に残った1人を釈放する。」
この問題そのものはあまりハッピーなものではない。
n=10 k=2 の場合については、以下の通りとなる。
結局、この場合には数字の「6」が最後まで残ることになる。
このように徐々に篩をかけていって、最後まで残る人はまさに「幸運(Lucky)」だということになる。このことから、類似の手法(無限の数を対象としており、カウントアウト(除外)のルールは異なっている)で生き残ることになる数字が「幸運数(lucky number)」と名付けられている。
なお、論文の著者の1人であるStanislaw Ulamは、ポーランド出身の米国の数学者で、自然数を渦巻状に並べた際の素数のパターン「ウラムの螺旋」で有名である。さらに、「テラー=ウラム配置」と呼ばれる水爆の機構の発案者としてもその名を残している。加えて、モンテカルロ法の考案者(命名者は、ジョン・フォン・ノイマン)としても知られている。
このように徐々に篩をかけていって、最後まで残る人はまさに「幸運(Lucky)」だということになる。このことから、類似の手法(無限の数を対象としており、カウントアウト(除外)のルールは異なっている)で生き残ることになる数字が「幸運数(lucky number)」と名付けられている。
なお、論文の著者の1人であるStanislaw Ulamは、ポーランド出身の米国の数学者で、自然数を渦巻状に並べた際の素数のパターン「ウラムの螺旋」で有名である。さらに、「テラー=ウラム配置」と呼ばれる水爆の機構の発案者としてもその名を残している。加えて、モンテカルロ法の考案者(命名者は、ジョン・フォン・ノイマン)としても知られている。
「幸運数」も無数に存在する
幸運数は無数に存在し、そのうち最小の数は 1 であるが、100以下の幸運数を 1 から小さい順に列挙すると、以下の通りとなる。
1、3、7、9、13、15、21、25、31、33、37、43、49、51、63、67、69、73、75、79、87、93、 99、 …
なお、幸運数は、その定義から、素数と性質を共有する部分がある。幸運数の現われ方は素数定理に近いものがあり、以前の研究員の眼で紹介した「ゴールドバッハの予想」は幸運数に対しても拡張される。つまり「4 以上の偶数は 2 個の幸運数の和として表せる」という予想が考えられている。ただし、これについても現在のところ証明されていない。
幸運数についても、幸運数かつ素数な数(lucky prime)が無数に存在するかどうかは分かっていない。
1、3、7、9、13、15、21、25、31、33、37、43、49、51、63、67、69、73、75、79、87、93、 99、 …
なお、幸運数は、その定義から、素数と性質を共有する部分がある。幸運数の現われ方は素数定理に近いものがあり、以前の研究員の眼で紹介した「ゴールドバッハの予想」は幸運数に対しても拡張される。つまり「4 以上の偶数は 2 個の幸運数の和として表せる」という予想が考えられている。ただし、これについても現在のところ証明されていない。
幸運数についても、幸運数かつ素数な数(lucky prime)が無数に存在するかどうかは分かっていない。
まとめ
今回は、特徴的な名称を有する「ハッピー数」と「幸運数」について、紹介した。
これによれば、いずれの概念にも「7」という数字が該当していることになる。すなわち、「7」は数学的にも「ハッピー」で「幸運」な数である、いうことになる。なかなか面白いと感じないだろうか。「7」という数字の持つ意味合いについては、次回の研究員の眼で詳しく報告する予定である。
これからも、こうした興味深い数字の紹介を行っていきたい。これを通じて、少しでも数学や数字に興味・関心を持っていただければと思っている。
これによれば、いずれの概念にも「7」という数字が該当していることになる。すなわち、「7」は数学的にも「ハッピー」で「幸運」な数である、いうことになる。なかなか面白いと感じないだろうか。「7」という数字の持つ意味合いについては、次回の研究員の眼で詳しく報告する予定である。
これからも、こうした興味深い数字の紹介を行っていきたい。これを通じて、少しでも数学や数字に興味・関心を持っていただければと思っている。
(2020年04月03日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年11月07日
次回の利上げは一体いつか?~日銀金融政策を巡る材料点検 -
2025年11月07日
個人年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年11月07日
中国の貿易統計(25年10月)~輸出、輸入とも悪化。対米輸出は減少が続く -
2025年11月07日
英国金融政策(11月MPC公表)-2会合連続の据え置きで利下げペースは鈍化 -
2025年11月06日
世の中は人間よりも生成AIに寛大なのか?
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「ハッピー数」や「幸運数」という名前の数字があるってこと知っていますか?】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「ハッピー数」や「幸運数」という名前の数字があるってこと知っていますか?のレポート Topへ


















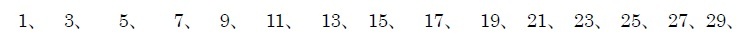
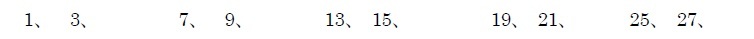
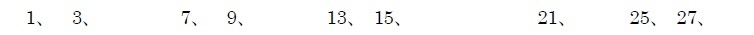

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




