- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 黄金比φについて(その1)-黄金比とはどのようなものなのか-
コラム
2020年11月10日
文字サイズ
- 小
- 中
- 大
はじめに
「黄金比」という言葉については、一度は耳にされたことがあると思う。また、その黄金比が社会のいろいろな場面で使用され、現われてくることをご存知の方も少なからずいらっしゃるものと思われる。
今回は、その「黄金比」に関連するテーマについて、2回に分けて触れてみたい。まずは、今回は、その定義及び関連した概念や歴史等について説明し、次回に、その「黄金比」がどのようなところで使用され、現れてくるのかについて報告する。なお、「黄金比」とは別の「貴金属比」である「白銀比」等や「黄金比」と深く関連している「フィボナッチ数列」については、別途報告することにしたい。
今回は、その「黄金比」に関連するテーマについて、2回に分けて触れてみたい。まずは、今回は、その定義及び関連した概念や歴史等について説明し、次回に、その「黄金比」がどのようなところで使用され、現れてくるのかについて報告する。なお、「黄金比」とは別の「貴金属比」である「白銀比」等や「黄金比」と深く関連している「フィボナッチ数列」については、別途報告することにしたい。
黄金比とは
と表されることになる。
1 「τ(タウ)」という記号が使用されることもあるが、「τ」は次々回の研究員の眼で説明する「白銀比」で使用されることが多いようだ。
1 「τ(タウ)」という記号が使用されることもあるが、「τ」は次々回の研究員の眼で説明する「白銀比」で使用されることが多いようだ。
黄金比の意味するところ
2 フィボナッチ数列(Fibonacci sequence) (Fn) は、次の漸化式で定義される数列である。
F0 = 0,F1 = 1,Fn+2 = Fn + Fn+1 (n ≥ 0)
なお、φ2-φ-1=0 より、φ―1/φ=1となることから、φとその逆数の1/φは、小数点以下は同じ数が続くことになる。
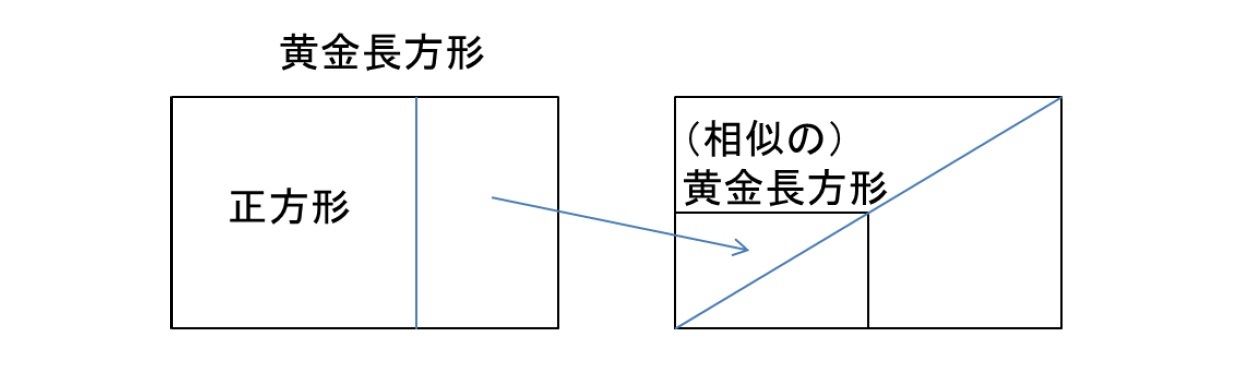
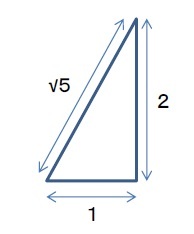
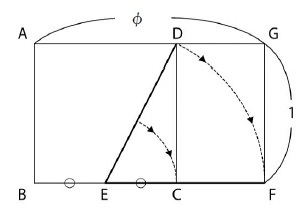
黄金長方形
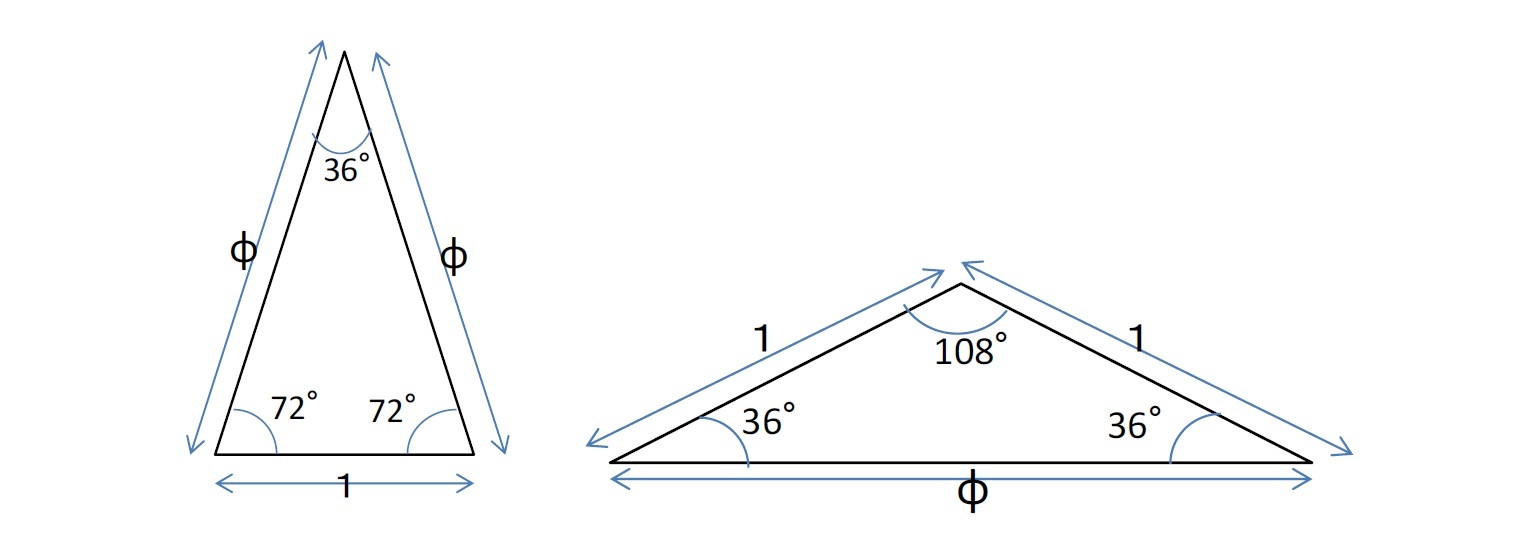
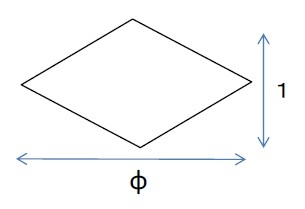
黄金三角形
黄金数の長さの作成
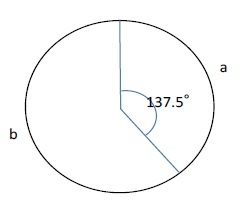
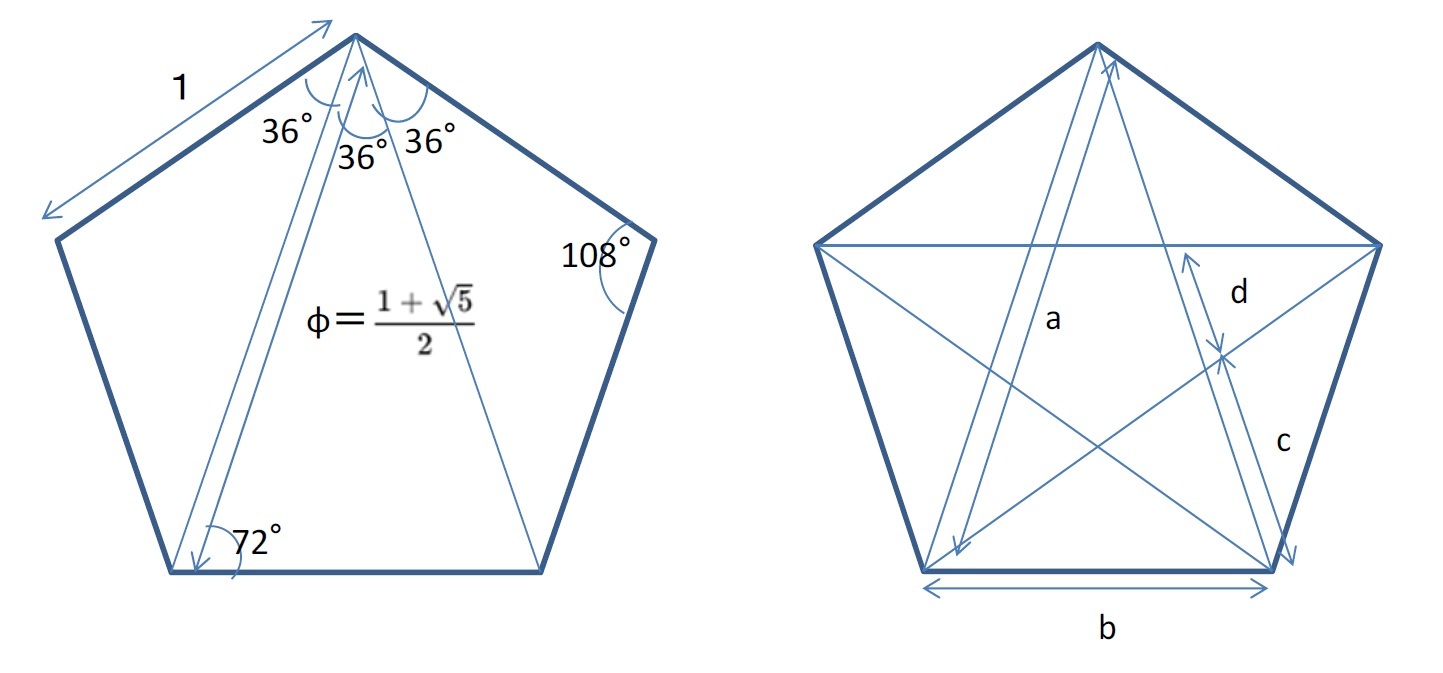
正五角形
さらに、「対角線同志の交点は、それぞれの対角線を黄金比に分割する」という点も挙げられる。正五角形の対角線によって、正五角形の中に五角の星形が作成されるが、これは「五芒星(ごぼうせい)」あるいは「ペンタグラム(pentagram)」や「ペンタルファ(pentalpha)」と呼ばれる。
この図形において、例えばa/b、b/c、c/dは全て黄金比となる。このため、「五芒星」は美しい図形であるとして、歴史的にもまた現代のデザイン等でもよく使用されている。例えば、米国の国旗である星条旗等の国旗にも五芒星が見られる。
五芒星は、一筆書きが可能な図形としてもよく知られている。
この図形において、例えばa/b、b/c、c/dは全て黄金比となる。このため、「五芒星」は美しい図形であるとして、歴史的にもまた現代のデザイン等でもよく使用されている。例えば、米国の国旗である星条旗等の国旗にも五芒星が見られる。
五芒星は、一筆書きが可能な図形としてもよく知られている。
正多面体等に見られる黄金比
正多面体(regular polyhedron)と呼ばれるものは、「全ての面が同一の正多角形で構成され、かつ全ての頂点において接する面の数が等しい凸多面体のこと」をいう。正多面体には正四面体、正六面体、正八面体、正十二面体、正二十面体の五種類しかない。これについては、以前の研究員の眼「サッカーボールは球形なのか-馴染み深い白黒のサッカーボールは、切頂二十面体と呼ばれるものがベースだってこと知っていましたか-」(2018.6.11)でその証明を紹介した。
この正多面体においては、表面的には黄金比はみられないが、正十二面体の面は正五角形になっていることから、先に述べたように黄金比が内在していることになる。加えて、この正十二面体、さらには正二十面体の表面積や体積には黄金比φが現れてくることになる。
この正多面体においては、表面的には黄金比はみられないが、正十二面体の面は正五角形になっていることから、先に述べたように黄金比が内在していることになる。加えて、この正十二面体、さらには正二十面体の表面積や体積には黄金比φが現れてくることになる。
黄金比の歴史
黄金比については、古代ギリシアの彫刻家ペイディアス(又はフェイディアス 、英語でPheidias、ギリシア語でΦειδίας)が初めて使ったと言われており、黄金数の記号「φ」は彼の名前の頭文字に由来している。ペイディアスは、ギリシアのパルテノン神殿を建築した人物として有名で、実際にパルテノン神殿を正面から見た場合の縦と横の比等に黄金比が使用されている。
古代ギリシアの数学者ユークリッドの著書「ユークリッド原論」の第6巻では、先の線分におけるaとbの関係に基づいた「外中比」の定義として、「線分を外中比に分ける方法」が記されている。
古代ギリシアより、西洋ではこの比率は「神聖なる比」として、崇められてきたと言われている。
「黄金比」という言葉が使用されるようになったのは、19世紀になってからで、まずはドイツの数学者マルティン・オーム(Martin Ohm)が1835年の「初等純粋数学(Die reine Elementar Mathematik)」で「黄金分割(goldener Schnitt)」という用語を使用したとされている。「黄金比(golden ratio)」の用語については、その後、英国の心理学者であるジェームズ・サリー(James Sully)が美学関連で使用し、スコットランドの数学者であるジョージ・クリスタル(George Chrystal)が初めて数学的な意味合いで使用したとされている。
なお、黄金比に対する数学定数「φ」に使用については、研究員の眼「数学記号の由来について」シリーズの中で触れることとする。
古代ギリシアの数学者ユークリッドの著書「ユークリッド原論」の第6巻では、先の線分におけるaとbの関係に基づいた「外中比」の定義として、「線分を外中比に分ける方法」が記されている。
古代ギリシアより、西洋ではこの比率は「神聖なる比」として、崇められてきたと言われている。
「黄金比」という言葉が使用されるようになったのは、19世紀になってからで、まずはドイツの数学者マルティン・オーム(Martin Ohm)が1835年の「初等純粋数学(Die reine Elementar Mathematik)」で「黄金分割(goldener Schnitt)」という用語を使用したとされている。「黄金比(golden ratio)」の用語については、その後、英国の心理学者であるジェームズ・サリー(James Sully)が美学関連で使用し、スコットランドの数学者であるジョージ・クリスタル(George Chrystal)が初めて数学的な意味合いで使用したとされている。
なお、黄金比に対する数学定数「φ」に使用については、研究員の眼「数学記号の由来について」シリーズの中で触れることとする。
(2020年11月10日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【黄金比φについて(その1)-黄金比とはどのようなものなのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
黄金比φについて(その1)-黄金比とはどのようなものなのか-のレポート Topへ




















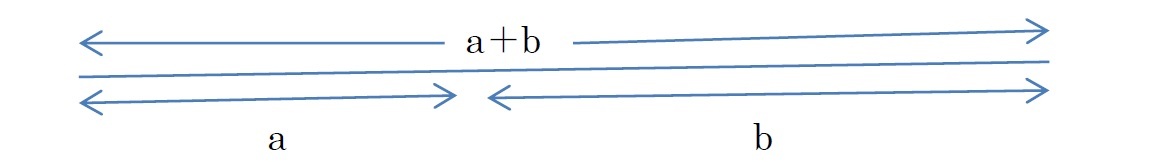
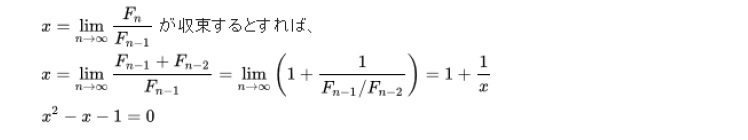


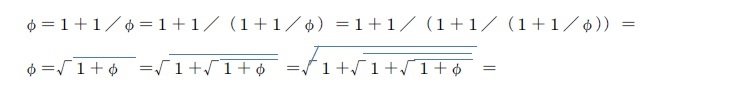

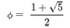
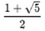

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




