- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 数学記号の由来について(7)-三角関数(sin、cos、tan等)-
コラム
2020年10月09日
文字サイズ
- 小
- 中
- 大
はじめに
何回かに分けて、これまで慣れ親しんできた数学で使用されている記号の由来について、報告している1。
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等、第6回目は、無限大(∞)、比例(∝)、相似(∽)等について報告した。
今回は、前回の研究員の眼で三角関数(sin、cos、tan等)の説明をしたので、その記号の由来等について報告する。なお、三角関数(sin、cos、tan等)のそれぞれの定義等については、研究員の眼「「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-」(2020.9.8)を参照していただきたい。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等、第6回目は、無限大(∞)、比例(∝)、相似(∽)等について報告した。
今回は、前回の研究員の眼で三角関数(sin、cos、tan等)の説明をしたので、その記号の由来等について報告する。なお、三角関数(sin、cos、tan等)のそれぞれの定義等については、研究員の眼「「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-」(2020.9.8)を参照していただきたい。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
「sin」(正弦)記号の使用及び由来
「sin(サイン)」という記号は、「sinusoid(正弦曲線)」からきているが、sinusoidは「sinus」(曲がり、湾曲、湾)と「oid」(のような、に似た)と言う意味を有している。なお、「sinus」は、元々はラテン語で、同じく「曲面、曲線、湾」という意味を有している。
この「sin」という記号については、Cajoriによれば、1583年にデンマークの数学者であるトーマス・フィンケ(Thomas Fincke)がその著書「Geometria rotundi」で、「sin.」と短縮を示す意味での「.(ピリオド)」付きで使用しており、これが最初の三角関数の略語の使用であるとしている。その後、1624年に計算尺の発明で知られる英国の数学者であるエドマンド・ガンター(Edmund Gunter)がガンター尺を表す図の中で「sin」というピリオド無しの記号を使用したとされるが、同じ年に発行された彼の論文ではこの記号は使用されなかったとのことである。結局、1632年に、以前の研究員の眼「数学記号の由来について(1)-四則演算の記号(+、-、×、÷)-」において、「×」の記号を最初に使用した等として紹介してきたウイリアム・オートレッド(William Oughtred)が、その著書「Addition vnto the Vse of the Instrvment called the Circles of Proportion」の中で「sin」を使用し、これが最初の使用だと言われているようだ。
この「sin」という記号については、Cajoriによれば、1583年にデンマークの数学者であるトーマス・フィンケ(Thomas Fincke)がその著書「Geometria rotundi」で、「sin.」と短縮を示す意味での「.(ピリオド)」付きで使用しており、これが最初の三角関数の略語の使用であるとしている。その後、1624年に計算尺の発明で知られる英国の数学者であるエドマンド・ガンター(Edmund Gunter)がガンター尺を表す図の中で「sin」というピリオド無しの記号を使用したとされるが、同じ年に発行された彼の論文ではこの記号は使用されなかったとのことである。結局、1632年に、以前の研究員の眼「数学記号の由来について(1)-四則演算の記号(+、-、×、÷)-」において、「×」の記号を最初に使用した等として紹介してきたウイリアム・オートレッド(William Oughtred)が、その著書「Addition vnto the Vse of the Instrvment called the Circles of Proportion」の中で「sin」を使用し、これが最初の使用だと言われているようだ。
「cos(コサイン)」(余弦)記号の使用及び由来
「cos(コサイン)」という記号は、cosineであり、co-sineということであり、「sin」に、補足的・補完的(complementary)の意味を有する接頭辞「co」を付したもので、「余角(complementary angle、co-angle)」(角度θに対する(90°-θ))に対する「sin」との意味合いを有している。
この「cos」という記号については、先のトーマス・フィンケ(Thomas Fincke)の「Geometria rotundi」では、「cos.」ではなく、「com.」が使用されていた。1674年には、英国の数学者であるジョナス・ムーア(Sir Jonas Moore)が「Mathematical Compendium」で「Cos.」を使用し、サミュエル・ジーク(Samuel Jeake)が「cos.」を使用したとされる。
Cajoriによれば、「cos」を最初に使用したのは、1729年にレオンハルト・オイラー(Leonhard Euler)が「Commentarii Academiae Scient. Petropollitanae, ad annum 1729」においてである、とされているようだ。
この「cos」という記号については、先のトーマス・フィンケ(Thomas Fincke)の「Geometria rotundi」では、「cos.」ではなく、「com.」が使用されていた。1674年には、英国の数学者であるジョナス・ムーア(Sir Jonas Moore)が「Mathematical Compendium」で「Cos.」を使用し、サミュエル・ジーク(Samuel Jeake)が「cos.」を使用したとされる。
Cajoriによれば、「cos」を最初に使用したのは、1729年にレオンハルト・オイラー(Leonhard Euler)が「Commentarii Academiae Scient. Petropollitanae, ad annum 1729」においてである、とされているようだ。
「tan(タンジェント)」(正接)記号の使用及び由来
「tan(タンジェント)」という記号は、接しているという意味を有する「tangent」からきており、これはラテン語の「tangere tango」(接する)に基づいている。
この「tan」という記号についても、先のトーマス・フィンケ(Thomas Fincke)が同じその著書「Geometria rotundi」で、「tan.」と「.(ピリオド)」付きで使用していた。 その後、ウイリアム・オートレッド(William Oughtred)が、その著書「The Circles of Proportion」の中で「tan」を使用し、これが最初の使用だと言われているようだ。
この「tan」という記号についても、先のトーマス・フィンケ(Thomas Fincke)が同じその著書「Geometria rotundi」で、「tan.」と「.(ピリオド)」付きで使用していた。 その後、ウイリアム・オートレッド(William Oughtred)が、その著書「The Circles of Proportion」の中で「tan」を使用し、これが最初の使用だと言われているようだ。
なぜ、日本語で「正弦」、「余弦」、「正接」と呼ばれるのか
「弦」と訳すのはよいとして、英語の「sin」と「cosine」の関係から,前者をもとの正の弦として「正弦」と呼び、後者を余角に対する弦という意味で「余弦」と呼んでいる。なお、英語の意味合いからは「補弦」という呼び方もあったかもしれないが、「余角」(角度θに対する(90°-θ))に対するものであり、「補角」(角度θに対する(180°-θ))に対するものではないことから、「余弦」と名付けられている。
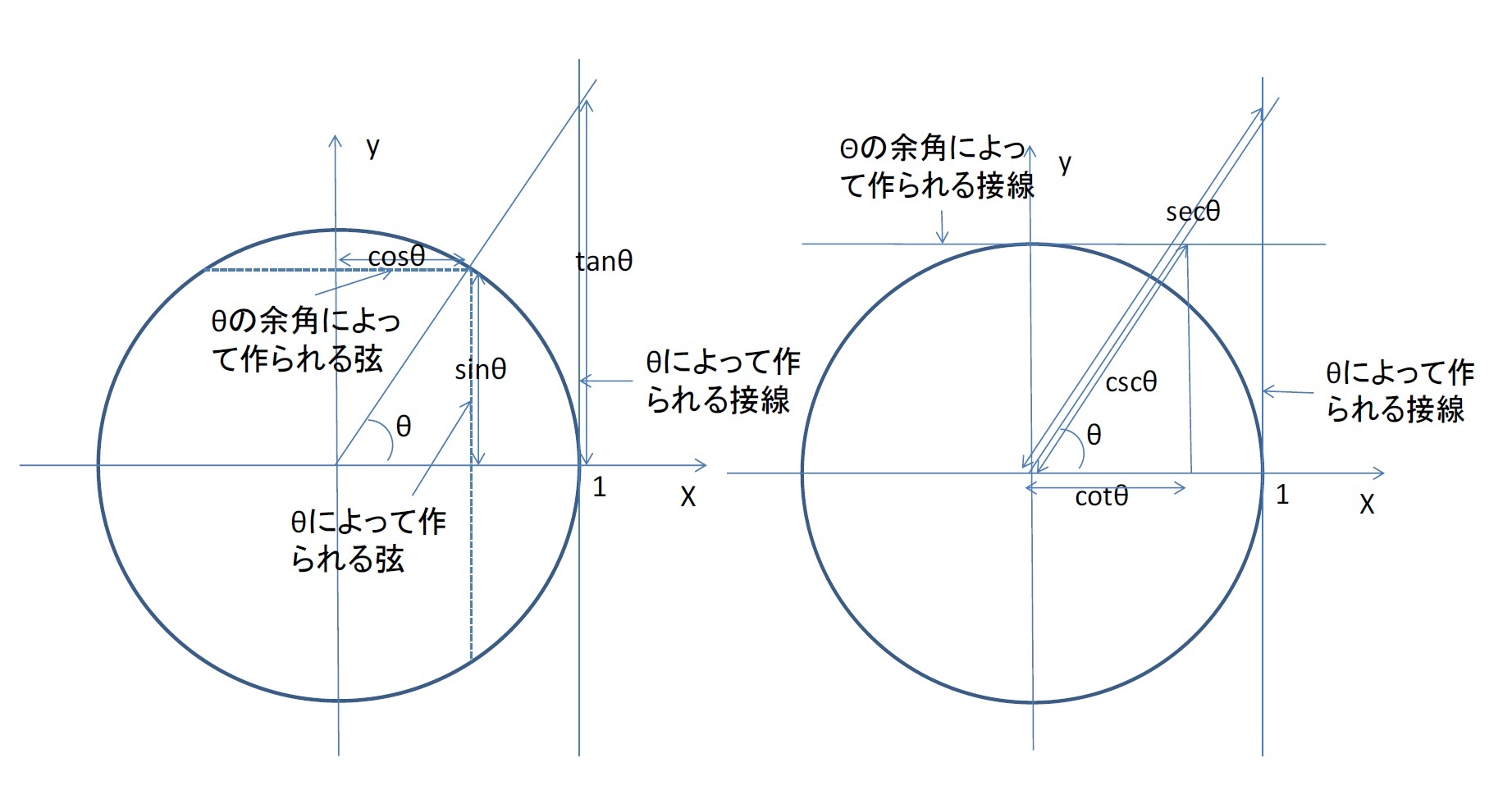
なお、x軸の正の部分と反時計回りになす角をθとしたとき、その中心角θが切り取る弦(実際には弦の半分(半弦)、以下同様)を「正弦」、θの余角(90°-θ)によって作られる弦を「余弦」といい、中心角θによって切り取られる接線の長さを「正接」ということになる(以下の左図の通り)。
なお、x軸の正の部分と反時計回りになす角をθとしたとき、その中心角θが切り取る弦(実際には弦の半分(半弦)、以下同様)を「正弦」、θの余角(90°-θ)によって作られる弦を「余弦」といい、中心角θによって切り取られる接線の長さを「正接」ということになる(以下の左図の通り)。
「sec(セカント)」(正割)記号の使用と由来
「sec(セカント)」は、「正割」と呼ばれ、三角比における余弦(cosine)の逆数、または円の割線のその円の半径に対する割合、を指している。「割線」とは、円の中心からある円弧の一方の端を通り、円弧のもう一方の端の接線と交わる点までの直線のことをいう(上記の右図の通り、以下同様)。
「sec(セカント)」は、切る、分ける、という意味を有する「secant」からきている。
この「sec」という記号については、トーマス・フィンケ(Thomas Fincke)の「Geometria rotundi」では、「sec.」と「.(ピリオド)」付きで使用されていた。その後、ウイリアム・オートレッド(William Oughtred)が、その著書「The Circles of Proportion」の中で「sec」を使用し、これが最初の使用だと言われているようだ。
「sec(セカント)」は、切る、分ける、という意味を有する「secant」からきている。
この「sec」という記号については、トーマス・フィンケ(Thomas Fincke)の「Geometria rotundi」では、「sec.」と「.(ピリオド)」付きで使用されていた。その後、ウイリアム・オートレッド(William Oughtred)が、その著書「The Circles of Proportion」の中で「sec」を使用し、これが最初の使用だと言われているようだ。
「csc又はcosec(コセカント)」(余割)記号の使用と由来
「csc(コセカント)」は、「余割」と呼ばれ、三角比における正弦(sin)の逆数、を指している。その名前が示す通りに、余角に対する割線の円の半径に対する割合を示している。
この「csc(コセカント)」については、トーマス・フィンケ(Thomas Fincke)の「Geometria rotundi」では、「sec.com」が使用されていた。その後、「cosec.」や「cosec:」といった表記も使用されたが、「csc」の最初の使用は1881年になってからのようだ。
この「csc(コセカント)」については、トーマス・フィンケ(Thomas Fincke)の「Geometria rotundi」では、「sec.com」が使用されていた。その後、「cosec.」や「cosec:」といった表記も使用されたが、「csc」の最初の使用は1881年になってからのようだ。
「cot(コタンジェント)」(余接)記号の使用と由来
「cot(コタンジェント)」は、「余接」と呼ばれ、三角比における正接(tan)の逆数、を指している。θの余角によって切り取られる接線の長さを示している。
この「cot(コタンジェント)」については、トーマス・フィンケ(Thomas Fincke)の「Geometria rotundi」では、「tan.com」が使用されていた。その後、「Cot.」や「cot.」といった表記も使用されたが、「cot」の最初の使用は1758年になってからのようだ。
この「cot(コタンジェント)」については、トーマス・フィンケ(Thomas Fincke)の「Geometria rotundi」では、「tan.com」が使用されていた。その後、「Cot.」や「cot.」といった表記も使用されたが、「cot」の最初の使用は1758年になってからのようだ。
逆三角関数記号の使用と由来
逆三角関数(inverse trigonometric function)というのは、三角関数の逆関数(いわゆる、y=f(x)に対してx=f-1(y)で表されるもの)で、sin-1 、cos-1、tan-1やarcsin、arccos、arctan等で表現されるものである。これらは角度の任意の三角比から角度を得るため等に使用される。
逆三角関数の記号については、1729年にダニエル・ベルヌーイ(Daniel Bernoulli)が「Comment. acad. sc. Petrop」の中で、arcsineに対して「AS」を使用した。さらに、レオンハルト・オイラー(Leonhard Euler)が1736年にarctangentに対して「At」を、1737年にarcsineに対して「A」を使用する等、その後も異なる数学者等がいろいろな記号を使用した。
Cajoriによると、最初に「-1」を導入したのは、1813年に英国の数学者であるジョン・フレデリック・ウィリアム・ハーシェル(John Frederick William Herschel)によってだった。完全な脚注が「cos-1e」のような使用の説明を行っていた。さらに、フランスにおいてJules Houëlが「arcsin」を使用した。
なお、1914年のジョージ・ウェントワース(George Wentworth) とデビッド・オイゲン・スミス(David Eugene Smith)による「Plane Trigonometry」の中では、「米国や英国の本では、記号sin-1 yが一般的に使用されている。欧州大陸では、arcsin yが使用されている。」と記述されている。
逆三角関数の記号については、1729年にダニエル・ベルヌーイ(Daniel Bernoulli)が「Comment. acad. sc. Petrop」の中で、arcsineに対して「AS」を使用した。さらに、レオンハルト・オイラー(Leonhard Euler)が1736年にarctangentに対して「At」を、1737年にarcsineに対して「A」を使用する等、その後も異なる数学者等がいろいろな記号を使用した。
Cajoriによると、最初に「-1」を導入したのは、1813年に英国の数学者であるジョン・フレデリック・ウィリアム・ハーシェル(John Frederick William Herschel)によってだった。完全な脚注が「cos-1e」のような使用の説明を行っていた。さらに、フランスにおいてJules Houëlが「arcsin」を使用した。
なお、1914年のジョージ・ウェントワース(George Wentworth) とデビッド・オイゲン・スミス(David Eugene Smith)による「Plane Trigonometry」の中では、「米国や英国の本では、記号sin-1 yが一般的に使用されている。欧州大陸では、arcsin yが使用されている。」と記述されている。
最後に
今回は、三角関数(sin、cos、tan等)の記号の由来等について報告した。
三角関数の記号については、基本的にはその意味する用語の略語から来ているので、比較的理解しやすいかもしれない。ただし、そうした三角関数の記号であっても、現在の記号に定着するまでには、一定の変遷を経ていることがわかった。当初は、短縮を示す意味での「.(ドット)」が付与されたりしていたが、こうした短縮記号が一定普及する中で、最終的には「.」が削除された現在の形に定着していったようである。
その意味で、欧米人にとっては、より受け入れやすい記号になっているものと思われる。三角関数については、日本語による名称も付与されており、これが本来的な意味合いを示しているものなのだが、こちらはむしろ一般の人にはあまり認識されていないように思われる。
この研究員の眼が、sin(サイン)、cos(コサイン)、tan(タンジェント)等の意味合いを再確認する契機になればと思う次第である。
三角関数の記号については、基本的にはその意味する用語の略語から来ているので、比較的理解しやすいかもしれない。ただし、そうした三角関数の記号であっても、現在の記号に定着するまでには、一定の変遷を経ていることがわかった。当初は、短縮を示す意味での「.(ドット)」が付与されたりしていたが、こうした短縮記号が一定普及する中で、最終的には「.」が削除された現在の形に定着していったようである。
その意味で、欧米人にとっては、より受け入れやすい記号になっているものと思われる。三角関数については、日本語による名称も付与されており、これが本来的な意味合いを示しているものなのだが、こちらはむしろ一般の人にはあまり認識されていないように思われる。
この研究員の眼が、sin(サイン)、cos(コサイン)、tan(タンジェント)等の意味合いを再確認する契機になればと思う次第である。
本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2020年10月09日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる -
2025年10月24日
企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年10月24日
消費者物価(全国25年9月)-コアCPI上昇率は拡大したが、先行きは鈍化へ -
2025年10月24日
保険業界が注目する“やせ薬”?-GLP-1は死亡率改善効果をもたらすのか -
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1)
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【数学記号の由来について(7)-三角関数(sin、cos、tan等)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数学記号の由来について(7)-三角関数(sin、cos、tan等)-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




