- シンクタンクならニッセイ基礎研究所 >
- 「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-
コラム
2020年09月08日
文字サイズ
- 小
- 中
- 大
はじめに
「三角関数」って何と言われると、多くの人が「サイン、コサイン、タンジェント」という用語を思い出すだろう。「三角関数」については、以前は義務教育の中学校でも教えていたようだが、今は高校になってから教えることになっているようだ。
実は「三角関数」というのは、社会で幅広く使用され、我々に馴染みの深い技術等に関係している極めて重要な概念である。今回は、これから何回かに分けて、この「三角関数」に関する話題を取り扱ってみたい。
実は「三角関数」というのは、社会で幅広く使用され、我々に馴染みの深い技術等に関係している極めて重要な概念である。今回は、これから何回かに分けて、この「三角関数」に関する話題を取り扱ってみたい。
「三角関数」と出会う機会
実は、多くの人にとって、「三角関数」を中学校あるいは高校等で学び、さらには大学の入学試験で数学の科目を受験しなければならなかった人は、「三角関数」に関する試験問題にかなり苦労したという苦い思い出があるのではないかと思われる。さらには、理工系の学部に進学した方々であれば、(もちろん、専門にもよるが)大学の授業においても三角関数を学ばなければならない機会があったものと思われる。
けれども、一旦高校や大学を卒業して、社会人生活に入ってしまうと、一部の人を除いた多くの人にとって、三角関数と出会う機会は殆どないものと思われる。かく言う私も、アクチュアリーという保険数理に関する専門家として、一応統計や確率等の数学に関わる職種についていながらも、この40年間近く、アクチュアリーの資格試験問題において出会った以外は、業務上三角関数に出会うことは、殆ど無かったものと思っている。
一方で、理工系の学部出身等で一部の業務に携わっている方々にとっては、三角関数は基本的なツールとなっており、その考え方を理解しておくことが極めて重要になっているのではないかと思われる。おそらくは、高校時代には「何のために勉強するのか」、「大学の入学試験のために必要だから」ぐらいに思っていたのが、大学に入学してからの専門での講義や社会人になってからの開発・研究等で必要不可欠になって、その有り難味(?)をしみじみと感じておられる方もいるのではないかと思われる。
今回の「三角関数」に関する研究員の眼のシリーズは、前者のような、どちらかといえば文系出身で社会人になってから三角関数に出会う機会のなかった方々を対象にしている。
けれども、一旦高校や大学を卒業して、社会人生活に入ってしまうと、一部の人を除いた多くの人にとって、三角関数と出会う機会は殆どないものと思われる。かく言う私も、アクチュアリーという保険数理に関する専門家として、一応統計や確率等の数学に関わる職種についていながらも、この40年間近く、アクチュアリーの資格試験問題において出会った以外は、業務上三角関数に出会うことは、殆ど無かったものと思っている。
一方で、理工系の学部出身等で一部の業務に携わっている方々にとっては、三角関数は基本的なツールとなっており、その考え方を理解しておくことが極めて重要になっているのではないかと思われる。おそらくは、高校時代には「何のために勉強するのか」、「大学の入学試験のために必要だから」ぐらいに思っていたのが、大学に入学してからの専門での講義や社会人になってからの開発・研究等で必要不可欠になって、その有り難味(?)をしみじみと感じておられる方もいるのではないかと思われる。
今回の「三角関数」に関する研究員の眼のシリーズは、前者のような、どちらかといえば文系出身で社会人になってから三角関数に出会う機会のなかった方々を対象にしている。
「三角関数」はどのように社会に役立っているのか
これから、「三角関数」に関する話題を述べていく前に、「三角関数」がどのように社会に役立っているのかについて簡単に触れておく(それぞれの詳しい内容については、また機会があれば紹介していきたいと思う)。
最も有名なのは「測量」においてだろう。歴史的な経緯からも、土地の測量やピラミッド等の建造物の高さ等を測定するために、三角関数の考え方が利用されてきた。
次には、三角関数は「波」ということに深く関係している。波には、いわゆる地震等に伴うものだけでなく、電波や光波や音波等、様々なものが含まれている。これらの調査・分析においては、三角関数が必須となっている。これによって、各種の音声処理や画像処理の技術が生まれ、これらが各種の放送や写真撮影、音楽再生等につながっていくことになる。
さらには、「振動」とも深く関係している。
このように、三角関数は、我々の社会と深く関わっており、なくてはならないものとなっている。
最も有名なのは「測量」においてだろう。歴史的な経緯からも、土地の測量やピラミッド等の建造物の高さ等を測定するために、三角関数の考え方が利用されてきた。
次には、三角関数は「波」ということに深く関係している。波には、いわゆる地震等に伴うものだけでなく、電波や光波や音波等、様々なものが含まれている。これらの調査・分析においては、三角関数が必須となっている。これによって、各種の音声処理や画像処理の技術が生まれ、これらが各種の放送や写真撮影、音楽再生等につながっていくことになる。
さらには、「振動」とも深く関係している。
このように、三角関数は、我々の社会と深く関わっており、なくてはならないものとなっている。
「三角関数」とは
まずは「三角関数」って、何だったけ、ということで、その説明から入ることにする。
「三角関数」は、いわゆる関数であるが、「平面三角法における、角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称である。」(Wikipedia)とされている。一般的に鋭角と呼ばれる90°未満の角度を扱う場合、三角関数の値は対応する直角三角形の二辺の長さの比であり、三角関数は「三角比」と呼ばれる。
三角関数には、以下の6つがある。
sin(sine、正弦)
sec(secant、正割)
tan(tangent、正接)
cos(cosine、余弦)
csc(cosecant、余割)
cot(cotangent、余接)
いわゆる、サイン(sine)、コサイン(cosine)、タンジェント(tangent)が有名であり、高校時代に学んだ記憶として残っているものは、主としてこれらだと思われるが、あまり馴染みがないかもしれないが、その他に3つの三角関数がある。
さらには、これらの三角関数の逆関数(いわゆる、y=f(x)に対してx=f-1(y)で表されるもの)として、sin-1 、cos-1、tan-1等も使用される。なお、三角関数の逆関数として −1 と添字する代わりに関数の頭に arc とつけることがある(たとえば sin の逆関数として sin−1 の代わりに arcsin を用いる)。
なお、これらの用語の由来等については、次回の研究員の眼で紹介することとする。
「三角関数」は、いわゆる関数であるが、「平面三角法における、角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称である。」(Wikipedia)とされている。一般的に鋭角と呼ばれる90°未満の角度を扱う場合、三角関数の値は対応する直角三角形の二辺の長さの比であり、三角関数は「三角比」と呼ばれる。
三角関数には、以下の6つがある。
sin(sine、正弦)
sec(secant、正割)
tan(tangent、正接)
cos(cosine、余弦)
csc(cosecant、余割)
cot(cotangent、余接)
いわゆる、サイン(sine)、コサイン(cosine)、タンジェント(tangent)が有名であり、高校時代に学んだ記憶として残っているものは、主としてこれらだと思われるが、あまり馴染みがないかもしれないが、その他に3つの三角関数がある。
さらには、これらの三角関数の逆関数(いわゆる、y=f(x)に対してx=f-1(y)で表されるもの)として、sin-1 、cos-1、tan-1等も使用される。なお、三角関数の逆関数として −1 と添字する代わりに関数の頭に arc とつけることがある(たとえば sin の逆関数として sin−1 の代わりに arcsin を用いる)。
なお、これらの用語の由来等については、次回の研究員の眼で紹介することとする。
「三角関数」の定義
実は、「三角関数」の定義には、いくつかのアプローチがあるが、以下では代表的な3つのケースについて紹介する。
1.直角三角形による定義
最も一般的に知られていて、高校時代等に学んだ記憶があるものは、これによるものだと思われる。
最も一般的に知られていて、高校時代等に学んだ記憶があるものは、これによるものだと思われる。
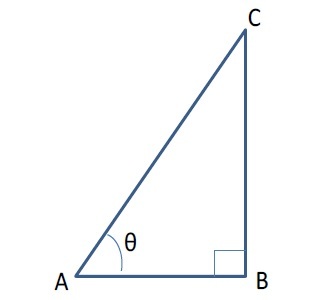 右のような直角三角形を考えた場合に、
右のような直角三角形を考えた場合に、sinθ=BC/AC
cosθ=AB/AC
tanθ=BC/AB
等と定義される。
ただし、この定義は直角三角形の鋭角に基づいているため、その定義域は θ が 0°から 90°まで(0(ラジアン)からπ / 2(ラジアン)まで)の範囲に限られることになる。また、θ = 90°(= π / 2)の場合 sec、tan が、θ = 0°(= 0) の場合 csc、cot が、それぞれ分母が0となることによって、定義されないことになる。
ただし、この定義は、最もシンプルで分かりやすく、まさに一般の人々の三角関数のイメージに沿ったものとなっている。次回以降に説明していく予定の各種の定理等を理解する上では、この定義によるもので、ある意味十分であると思われる。
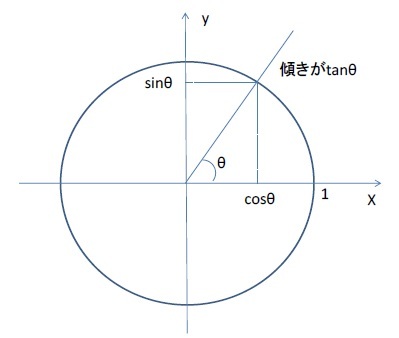
2.単位円による定義
右図のような半径1の円(単位円)を考える。
右図のような半径1の円(単位円)を考える。
この定義は、実数の範囲では単位円による定義と一致する。
この定義は、任意の複素数に対して定義されるので、「数学的には最もシンプルで汎用性のあるもの」となる。そのため、研究者にとっては「最も美しい(?)」ものになっているということになる。
この定義によれば、もはや角度という概念を介する必要がなくなる。
ただし、一般の人々にとっては、難しく、そのことを理解する必要性もあまりないものと思われる。
この定義は、任意の複素数に対して定義されるので、「数学的には最もシンプルで汎用性のあるもの」となる。そのため、研究者にとっては「最も美しい(?)」ものになっているということになる。
この定義によれば、もはや角度という概念を介する必要がなくなる。
ただし、一般の人々にとっては、難しく、そのことを理解する必要性もあまりないものと思われる。
まとめ
以上、今回は「三角関数」の定義について、紹介した。
最後の級数による定義は、かなり複雑な印象を与えるものになってしまったが、定義を拡張して一般化しようとすると、このようなことになってくる。
次回のこのシリーズでは、「三角関数の性質」として、高校時代に学んだいくつかの公式や定理等について、改めて見直してみたいと思う。
最後の級数による定義は、かなり複雑な印象を与えるものになってしまったが、定義を拡張して一般化しようとすると、このようなことになってくる。
次回のこのシリーズでは、「三角関数の性質」として、高校時代に学んだいくつかの公式や定理等について、改めて見直してみたいと思う。
(2020年09月08日「研究員の眼」)
このレポートの関連カテゴリ
関連レポート
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その2)-加法定理、二倍角、三倍角、半角の公式等-
- 「三角関数」と「波」の関係-三角関数による「波」の表現と各種の波(電磁波、音波、地震波等)-
- 「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-
- 「三角関数」と「フーリエ変換」-三角関数の幅広い実社会利用での基礎となる重要な数学的手法-
- 「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
| 2025/09/12 | 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月14日
今週のレポート・コラムまとめ【10/7-10/10発行分】 -
2025年10月10日
企業物価指数2025年9月~国内企業物価の上昇率は前年比2.7%、先行きは鈍化予想~ -
2025年10月10日
中期経済見通し(2025~2035年度) -
2025年10月10日
保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など -
2025年10月10日
若者消費の現在地(4)推し活が映し出す、複層的な消費の姿~データで読み解く20代の消費行動
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-のレポート Topへ


















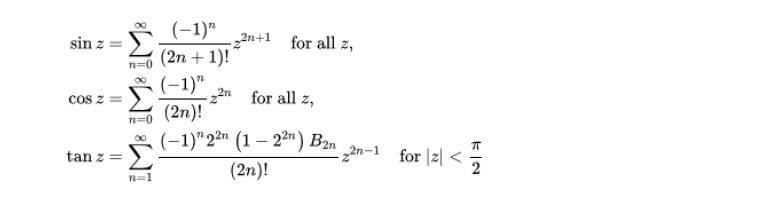

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




