- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-
コラム
2021年08月27日
文字サイズ
- 小
- 中
- 大
はじめに
これまで、三角関数については、研究員の眼「「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-」(2020.9.8)で、「三角関数」の定義について、研究員の眼「数学記号の由来について(7)-三角関数(sin、cos、tan等)-」(2020.10.9)では、三角関数の記号(sin、cos、tan等)の由来について紹介した。さらに、高校時代に学んだいくつかの公式や定理等のうち、「余弦定理」、「正弦定理」、「正接定理」、「加法定理」、「二倍角、三倍角、半角の公式」、「合成公式」、「和と積の変換公式」等について、その有用性を含めて紹介した。さらに、このシリーズの前回の研究員の眼では「三角関数」の社会での応用として、最も幅広い関わりがある「波」との関係について触れた。
今回の研究員の眼では、三角関数によって波が表現されることで、どのように社会で役立っているのかについて、具体的に電波によって、どのように情報が送信されていくのかを例にして報告する。
今回の研究員の眼では、三角関数によって波が表現されることで、どのように社会で役立っているのかについて、具体的に電波によって、どのように情報が送信されていくのかを例にして報告する。
波の三角関数による表現
そもそも、前回説明した「電磁波(electromagnetic wave)」や「音波(acoustic wave)」や「地震波(seismic wave、earthquake wave)」等の波がどのように表現されるのかが興味深いものと思われる。さらに、それらの波が本当に三角関数で表現できるのかが問題となってくる。
例えば、「電磁波」がどのような波になるのかについては、いわゆる電磁場を記述する基礎方程式である「マクスウェルの方程式」で支配される。一方で、「音波」や「地震波」等の力学的な波については、いわゆる「ニュートンの運動方程式」を含む「ニュートンの運動法則」で支配されることになる。
そして、これらの方程式や法則の下で形成される波については、「波動方程式(wave equation)」等で記述されることになる。
こうした方程式を解くことによって、上記で述べた一般的な波の基本形は、正弦関数(sin)を用いて、以下の算式で表現されることになる1。このように表現される波を「正弦波」2と総称している。
例えば、「電磁波」がどのような波になるのかについては、いわゆる電磁場を記述する基礎方程式である「マクスウェルの方程式」で支配される。一方で、「音波」や「地震波」等の力学的な波については、いわゆる「ニュートンの運動方程式」を含む「ニュートンの運動法則」で支配されることになる。
そして、これらの方程式や法則の下で形成される波については、「波動方程式(wave equation)」等で記述されることになる。
こうした方程式を解くことによって、上記で述べた一般的な波の基本形は、正弦関数(sin)を用いて、以下の算式で表現されることになる1。このように表現される波を「正弦波」2と総称している。
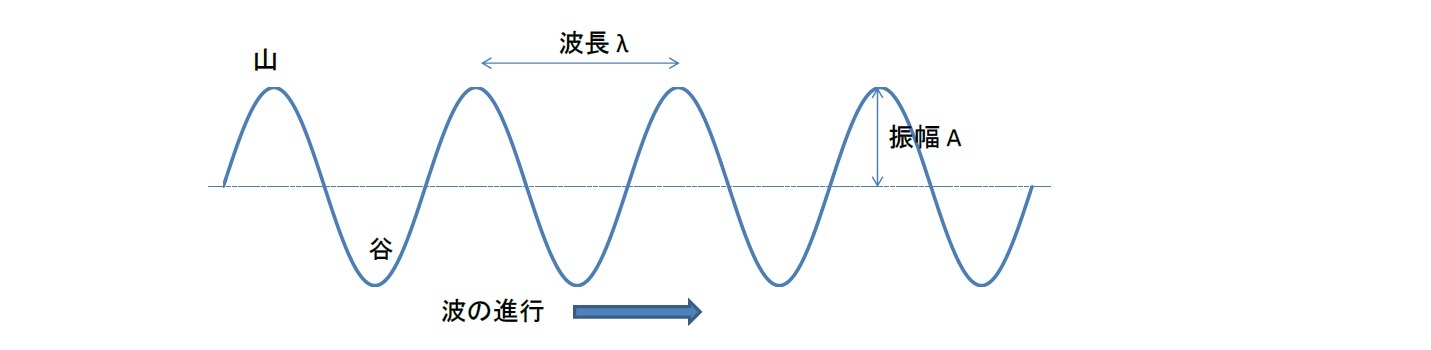
なお、このシリーズの前回の研究員の眼で、波には「縦波」と「横波」があり、電磁波は「横波」であるが、音波は「縦波」であり、地震波には「縦波」と「横波」があると報告した。
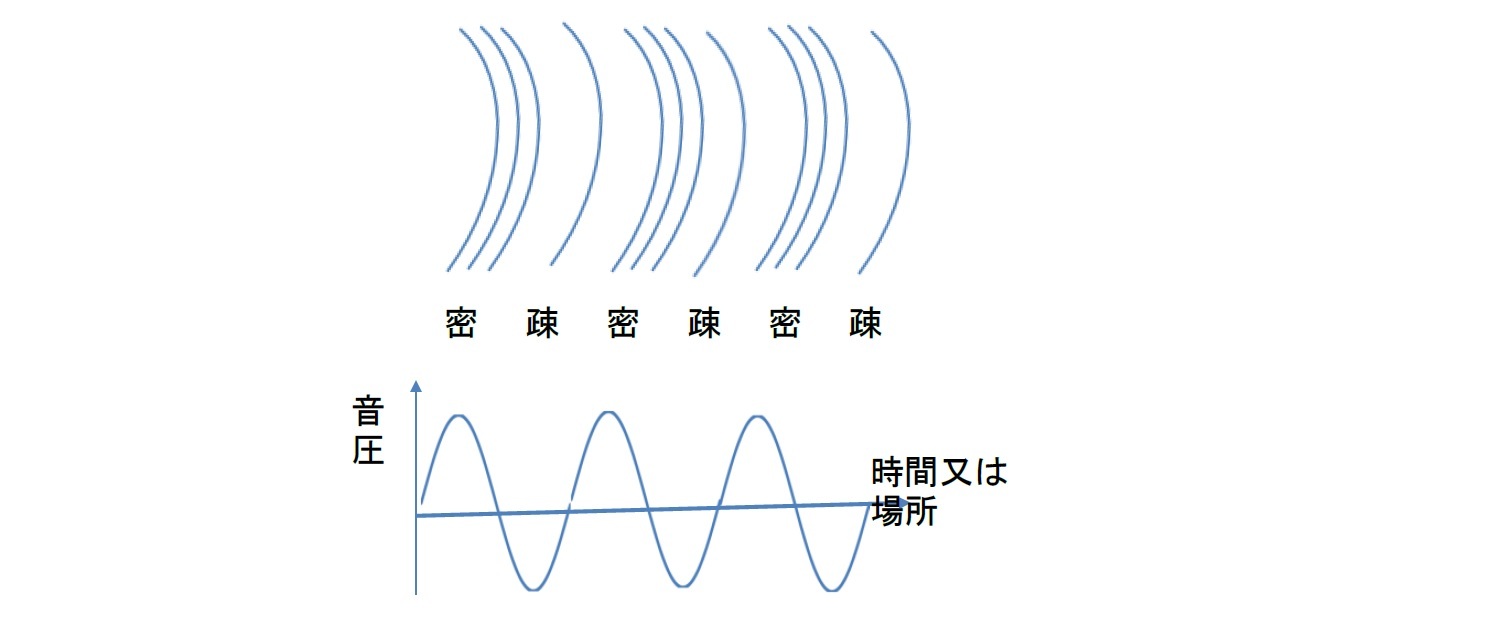
上記の波の図は、一般的に「横波」をイメージしたものになっている。「縦波」の場合には媒質の粗密で表されるため、必ずしも上記のイメージに沿ったものとはなっていない。ただし、例えば、音波の場合には、音圧(音による圧力の大気圧からの変動)や媒質の運動速度を縦軸にとり、時間や場所による変化を横軸にとることで、以下のように、横波と同じような波形で示されることになる。
上記の波の図は、一般的に「横波」をイメージしたものになっている。「縦波」の場合には媒質の粗密で表されるため、必ずしも上記のイメージに沿ったものとはなっていない。ただし、例えば、音波の場合には、音圧(音による圧力の大気圧からの変動)や媒質の運動速度を縦軸にとり、時間や場所による変化を横軸にとることで、以下のように、横波と同じような波形で示されることになる。
1 振幅の中心値が0ではなくて、Dとなる場合には、さらに「+D」が追加されることになる。
2 余弦関数(cos)の波形である「余弦波」についても、正弦波がシフトしたもの(cos x=sin(x+π/2))で波形が同一となることから、ここでは、これらを含めて、いわゆる「正弦波」による表現としている。
3 位相とは、波の山や谷の特定の位置
電波における周波数
真空中を進む電磁波の場合、その(位相)速度 v は(電磁波の分類によらず)光速 c(=約30万km/s(1秒間に地球を7周半する速さ))に等しくなる。従って、周波数と波長は反比例する形になっている(周波数が高くなると波長は短く、周波数が低くなると波長は長くなる)。
電波においては、周波数は1秒間に含まれる電波の数を示しており、周波数は「Hz(ヘルツ)」という単位で示される。
以下で説明するように、データを送信する場合には電波にデジタル信号のデータを載せていくことから、周波数が高いほどより多くのデータを送ることができることになり、通信速度が速くなる。一方で、周波数が高くなると電波の直進性が高くなるが、直進性が高くなると障害物の存在に対して弱くなり、電波の透過力も弱くなる。また、周波数が高くなるほど電波の振動が大きくなり、空気抵抗により減衰しやすくなるので、電波の伝送距離が減少することになる。
電波においては、周波数は1秒間に含まれる電波の数を示しており、周波数は「Hz(ヘルツ)」という単位で示される。
以下で説明するように、データを送信する場合には電波にデジタル信号のデータを載せていくことから、周波数が高いほどより多くのデータを送ることができることになり、通信速度が速くなる。一方で、周波数が高くなると電波の直進性が高くなるが、直進性が高くなると障害物の存在に対して弱くなり、電波の透過力も弱くなる。また、周波数が高くなるほど電波の振動が大きくなり、空気抵抗により減衰しやすくなるので、電波の伝送距離が減少することになる。
電波によるデータの送信
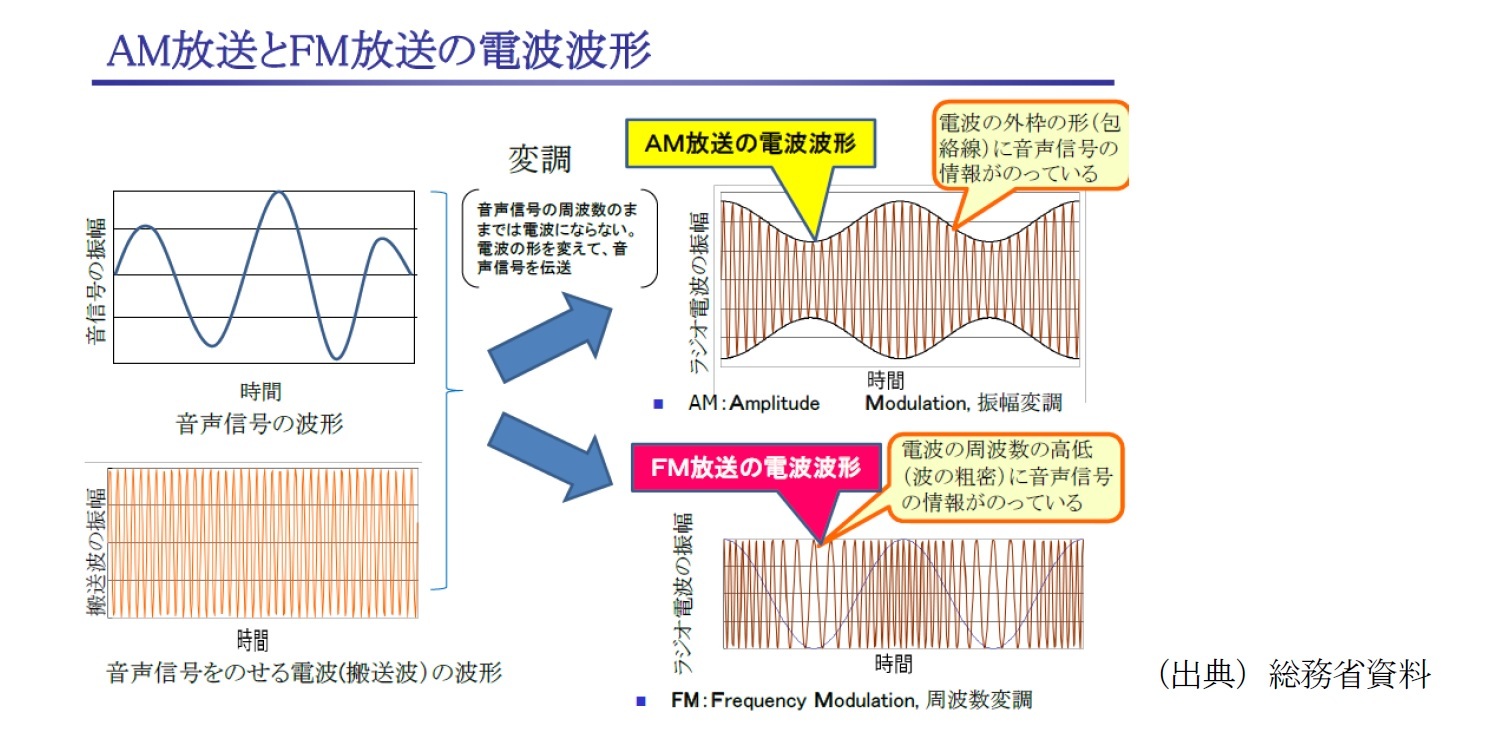
電波を使って通信を行う場合、一定の周波数の「搬送波」に対して、「変調4」と呼ばれる操作を行い、伝達したい情報を載せる。この変調された搬送波を「変調波」といい、この変調波を受信して、そこに乗せられている情報を取り出すことを「復調」と呼ぶ。また、搬送波に載せる情報は「ベースバンド信号」と呼ばれ、ラジオの場合には音声信号であり、デジタル通信ではデジタル信号となる。
4 アナログ通信のための「変調」には、さらに位相を変化させるPM(Phase Modulation(位相変調))がある。
4 アナログ通信のための「変調」には、さらに位相を変化させるPM(Phase Modulation(位相変調))がある。
AM放送とFM放送
なお、AMとFMを並行して使うこともできる。例えば、アナログ波では、AM信号で映像、FM信号で音声を送信していた。
アナログ信号とデジタル信号
「アナログ信号」は、連続的に電圧等が変化する信号で、いわゆる「正弦波」等のなだらかな波形で表現される。音声や映像を電波の波形にしてそのまま送るのが「アナログ信号」となる。
「デジタル信号」は、一定の電圧等を基準値(臨界値)にして、それを超える値を1、それ以下を0とすることで表す信号で、四角の形をした「矩形波(方形波)」で表現される。
「アナログ信号」はどのような値も取りうることから情報量が多いが、信号が減衰したり、他の電波の影響を受けて波形が乱れると、修復が難しい。これに対して、「デジタル信号」は周波数や波形の違いによる干渉が避けられるので、複数の情報を取り混ぜて送信ができることから、大量の情報を短時間に送信する必要がある高速通信に適している。現在は光ファイバーを使用して、「光信号」(デジタル信号の「オン(1)」と「オフ(0)」を光の点滅に情報を載せて送る信号)により、画像や動画といった大容量のデータ通信が可能となっている。
なお、2011年に日本のアナログ放送(アナログ信号の伝達を利用したテレビ放送)は終了し、デジタル放送(デジタル信号の伝達を利用したテレビ放送)に切り替わっている。この理由の1つとしては、携帯電話の爆発的な普及によって電波の周波数帯が飽和状態になったことが挙げられる。
デジタル放送の最大のメリットとして、信号を圧縮して、大量の情報をまとめて送信でき、テレビ放送の周波数帯をアナログ放送よりもコンパクトに纏めることが可能になったことが挙げられている。
「デジタル信号」は、一定の電圧等を基準値(臨界値)にして、それを超える値を1、それ以下を0とすることで表す信号で、四角の形をした「矩形波(方形波)」で表現される。
「アナログ信号」はどのような値も取りうることから情報量が多いが、信号が減衰したり、他の電波の影響を受けて波形が乱れると、修復が難しい。これに対して、「デジタル信号」は周波数や波形の違いによる干渉が避けられるので、複数の情報を取り混ぜて送信ができることから、大量の情報を短時間に送信する必要がある高速通信に適している。現在は光ファイバーを使用して、「光信号」(デジタル信号の「オン(1)」と「オフ(0)」を光の点滅に情報を載せて送る信号)により、画像や動画といった大容量のデータ通信が可能となっている。
なお、2011年に日本のアナログ放送(アナログ信号の伝達を利用したテレビ放送)は終了し、デジタル放送(デジタル信号の伝達を利用したテレビ放送)に切り替わっている。この理由の1つとしては、携帯電話の爆発的な普及によって電波の周波数帯が飽和状態になったことが挙げられる。
デジタル放送の最大のメリットとして、信号を圧縮して、大量の情報をまとめて送信でき、テレビ放送の周波数帯をアナログ放送よりもコンパクトに纏めることが可能になったことが挙げられている。
アナログ信号をデジタル信号に変換する仕組み
一般の音声信号やデータはアナログ信号であることから、これらをデジタル信号として送信するためには、これらをデジタル信号に変換(A/D変換あるいは符号化(エンコード))する必要がある。さらには、こうしたデジタル信号を受信しても、そのままでは意味をなさないことから、これらを再びアナログ信号に変換(D/A変換あるいは複合化(デコード))する必要がある。
符号化は、「標本化」と「量子化」というステップで行われる。
「標本化(サンプリング)」というのは、アナログ信号の波形を、ある一定の時間軸で区切って、その強度(波形の高さ)を測定することをいう。1秒間にサンプリングする回数を「サンプリング周波数」という。「シャノンのサンプリング定理」と呼ばれるものに基づいて、アナログ信号の約2倍の周波数でサンプリングが行われる(因みに、加入電話のサンプリング周波数は8kHz〈1秒間に8,000回〉となっている。
「量子化」というのは、サンプリングしたアナログ波形の強度を区分して、何段階で表現するのかというステップを指している。
即ち、標本化によって、横の時間軸上の近似化が行われ、量子化で縦の強度軸上の近似化が行われることになる。こうした方法を「パルス符号変調(PCM:Pulse Code Modulation)」という。
なお、実際にはこれらに加えて、「圧縮化」というステップが行われる。「圧縮化」というのは、負荷の負担を抑制するためのデジタル化によるビット数の削減方式で、例えば、人間の聴覚が小さな音の変化には敏感だが大きな音の変化には鈍感であることから、強度が大きいところでは量子化ステップを大きめに設定するような圧縮化が行われる。
なお、量子化で使用されるビット数を削減するために、全ての信号をデジタル化せずに、前の情報と異なる部分だけをデジタル化する方法もあり、これを「適応差分パルス符号変調(AD-PCM:Adaptive Differential Pulse Code Modulation)」と呼んでいる。
符号化は、「標本化」と「量子化」というステップで行われる。
「標本化(サンプリング)」というのは、アナログ信号の波形を、ある一定の時間軸で区切って、その強度(波形の高さ)を測定することをいう。1秒間にサンプリングする回数を「サンプリング周波数」という。「シャノンのサンプリング定理」と呼ばれるものに基づいて、アナログ信号の約2倍の周波数でサンプリングが行われる(因みに、加入電話のサンプリング周波数は8kHz〈1秒間に8,000回〉となっている。
「量子化」というのは、サンプリングしたアナログ波形の強度を区分して、何段階で表現するのかというステップを指している。
即ち、標本化によって、横の時間軸上の近似化が行われ、量子化で縦の強度軸上の近似化が行われることになる。こうした方法を「パルス符号変調(PCM:Pulse Code Modulation)」という。
なお、実際にはこれらに加えて、「圧縮化」というステップが行われる。「圧縮化」というのは、負荷の負担を抑制するためのデジタル化によるビット数の削減方式で、例えば、人間の聴覚が小さな音の変化には敏感だが大きな音の変化には鈍感であることから、強度が大きいところでは量子化ステップを大きめに設定するような圧縮化が行われる。
なお、量子化で使用されるビット数を削減するために、全ての信号をデジタル化せずに、前の情報と異なる部分だけをデジタル化する方法もあり、これを「適応差分パルス符号変調(AD-PCM:Adaptive Differential Pulse Code Modulation)」と呼んでいる。
(2021年08月27日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-のレポート Topへ


















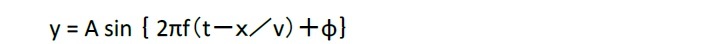

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




