- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「三角関数」と「フーリエ変換」-三角関数の幅広い実社会利用での基礎となる重要な数学的手法-
コラム
2021年11月10日
文字サイズ
- 小
- 中
- 大
はじめに
これまで、三角関数については、研究員の眼「「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-」(2020.9.8)で、「三角関数」の定義について、また、研究員の眼「数学記号の由来について(7)-三角関数(sin、cos、tan等)-」(2020.10.9)では、三角関数の記号(sin、cos、tan等)の由来について紹介した。そして、高校時代に学んだいくつかの公式や定理等のうち、「余弦定理」、「正弦定理」、「正接定理」、「加法定理」、「二倍角、三倍角、半角の公式」、「合成公式」、「和と積の変換公式」等について、その有用性を含めて紹介した。さらに、前回と前々回の研究員の眼(「三角関数」のシリーズ、以下同様)では「三角関数」の社会での応用として、最も幅広い関りがある「波」との関係について触れた。
今回の研究員の眼では、通常の波を三角関数によって表現するための数学的手法である「フーリエ級数展開」や「フーリエ変換」について、その概要を紹介する。その前段として、三角関数・指数関数・対数関数の微分・積分やべき級数転換、オイラーの公式を通じた対数・指数関数との関係等について簡単に紹介する。
今回の報告では、結果等の事実についてのみ紹介することとし、その証明等については行わない。また、あくまでもイメージを把握してもらうための概要に焦点を当てているため、細部等については必ずしも十分に正確ではないことを述べておく。これらの証明を含めたさらに詳しい細かい内容等について、興味・関心を抱いていただけた方々は、数多くの書籍等が出版されているので、それらを参照していただければと思っている。
今回の研究員の眼では、通常の波を三角関数によって表現するための数学的手法である「フーリエ級数展開」や「フーリエ変換」について、その概要を紹介する。その前段として、三角関数・指数関数・対数関数の微分・積分やべき級数転換、オイラーの公式を通じた対数・指数関数との関係等について簡単に紹介する。
今回の報告では、結果等の事実についてのみ紹介することとし、その証明等については行わない。また、あくまでもイメージを把握してもらうための概要に焦点を当てているため、細部等については必ずしも十分に正確ではないことを述べておく。これらの証明を含めたさらに詳しい細かい内容等について、興味・関心を抱いていただけた方々は、数多くの書籍等が出版されているので、それらを参照していただければと思っている。
これにより、例えば、正弦関数sin xの微分を繰り返すと、以下の通りとなる。
sin x → cos x → -sin x → -cos x → sin x
このように、正弦関数は4回微分すると、元の正弦関数に戻る。
また、eを底とする指数関数を微分しても、同じ指数関数となる。
sin x → cos x → -sin x → -cos x → sin x
このように、正弦関数は4回微分すると、元の正弦関数に戻る。
また、eを底とする指数関数を微分しても、同じ指数関数となる。
三角関数・指数関数・対数関数の積分
1 「0」を中心としたテイラー級数が「マクローリン級数」と呼ばれる。
この式は、上記のべき級数展開からも導き出される。
これにより、eixは、周期2πの周期関数となっていることがわかる。
これにより、eixは、周期2πの周期関数となっていることがわかる。
三角関数の直交性
2 関数は高校時代に学んだベクトルの一種(成分の数が無限個あるベクトルとみなすことができる)で、ベクトルが「直交」しているとは、その「内積が0」であること、即ち「成分の積の和が0」であることを意味している。sinとcosを複素平面上で示すことでイメージを有することができると思われる。
フーリエ級数
となる。これらを「フーリエ係数」と呼ぶ。
即ち、f(x)は、sin nx、cos nxという異なる周期を有する関数の線形結合で、係数anとbnがそれらの加重を示す指標になっている。
以前の研究員の眼で述べたように、一定の周期を有する「周期関数」については、「区分的に滑らかな」という条件を満たす場合には、単純な波動の数学的な表現である正弦関数や余弦関数の和としての「フーリエ級数」で表すことができることになる。さらには、周期関数ではない関数も、「区分的に滑らかで、かつ連続で、かつ絶対可積分(絶対値が積分可能)」という条件を満たす場合には、同様に三角関数で表現することができることになる。
前回の研究員の眼で紹介した「矩形波」や「のこぎり波」等の表現が、まさにこの「フーリエ級数」になっている。無限級数になっているのは、正弦波のような基本的な三角関数の波が曲線となっているのに対して、「矩形波」や「のこぎり波」のような直線を有する波を表現するためには、無限に足し合わせることが必要になってくるためである。もちろん、(波という意味において)単純な波は有限個の和(即ち、上記級数において、自然数Nが存在して、an=bn=0(n≧N))で表すことができる場合もある。
また、初項の「a0/2」は、「関数の平均値」を示している。「a0」も上記のanの算式でn=0 として得られるものであることから、結果的に「a0/2」という表現になってくる。
なお、有限な関数を無限級数で表現することで、本当に収束するのだろうかという疑問も当然に発生してくるものと思われる。これは、三角関数が正値と負値が交互に現れてくる周期関数であるということが関係していて、これらの和がお互いに打ち消しあっていく要素が大きいことになる。
即ち、f(x)は、sin nx、cos nxという異なる周期を有する関数の線形結合で、係数anとbnがそれらの加重を示す指標になっている。
以前の研究員の眼で述べたように、一定の周期を有する「周期関数」については、「区分的に滑らかな」という条件を満たす場合には、単純な波動の数学的な表現である正弦関数や余弦関数の和としての「フーリエ級数」で表すことができることになる。さらには、周期関数ではない関数も、「区分的に滑らかで、かつ連続で、かつ絶対可積分(絶対値が積分可能)」という条件を満たす場合には、同様に三角関数で表現することができることになる。
前回の研究員の眼で紹介した「矩形波」や「のこぎり波」等の表現が、まさにこの「フーリエ級数」になっている。無限級数になっているのは、正弦波のような基本的な三角関数の波が曲線となっているのに対して、「矩形波」や「のこぎり波」のような直線を有する波を表現するためには、無限に足し合わせることが必要になってくるためである。もちろん、(波という意味において)単純な波は有限個の和(即ち、上記級数において、自然数Nが存在して、an=bn=0(n≧N))で表すことができる場合もある。
また、初項の「a0/2」は、「関数の平均値」を示している。「a0」も上記のanの算式でn=0 として得られるものであることから、結果的に「a0/2」という表現になってくる。
なお、有限な関数を無限級数で表現することで、本当に収束するのだろうかという疑問も当然に発生してくるものと思われる。これは、三角関数が正値と負値が交互に現れてくる周期関数であるということが関係していて、これらの和がお互いに打ち消しあっていく要素が大きいことになる。
となる。
(2021年11月10日「研究員の眼」)
関連レポート
- 「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-
- 数学記号の由来について(7)-三角関数(sin、cos、tan等)-
- 数学記号の由来について(9)-数学定数(e、π、φ、i)-
- 数学記号の由来について(8)-「数」を表す記号-
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その2)-加法定理、二倍角、三倍角、半角の公式等-
- 「三角関数」と「波」の関係-三角関数による「波」の表現と各種の波(電磁波、音波、地震波等)-
- 「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
| 2025/09/12 | 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ- | 中村 亮一 | 研究員の眼 |
| 2025/09/02 | 欧州大手保険グループの2025年上期末SCR比率等の状況-ソルベンシーII等に基づく数値結果報告と資本管理等に関係するトピック- | 中村 亮一 | 基礎研レポート |
新着記事
-
2025年10月03日
長期再保険事業のストレステスト(バミューダ)-バミューダ金融当局の評価結果の公表 -
2025年10月03日
雇用関連統計25年8月-失業率、有効求人倍率ともに悪化 -
2025年10月03日
DB年金のそこにある危機 -
2025年10月03日
資本配分と成長投資 -
2025年10月03日
進む東証改革、なお残る上場維持基準の課題
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「三角関数」と「フーリエ変換」-三角関数の幅広い実社会利用での基礎となる重要な数学的手法-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「三角関数」と「フーリエ変換」-三角関数の幅広い実社会利用での基礎となる重要な数学的手法-のレポート Topへ


















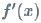 は、
は、


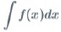
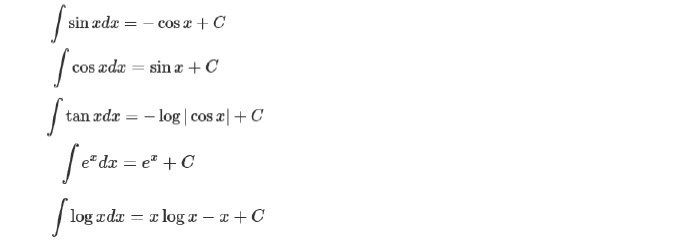


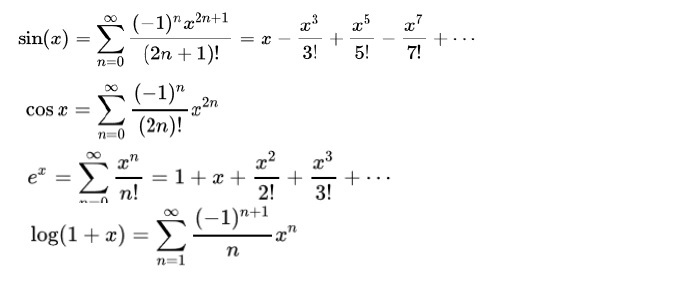


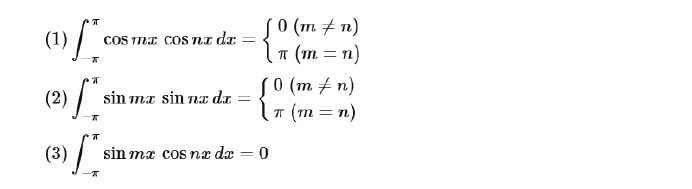
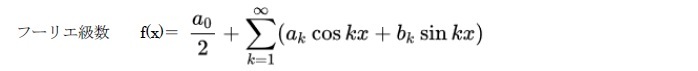
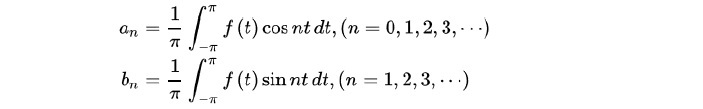

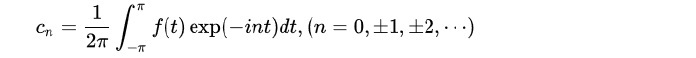
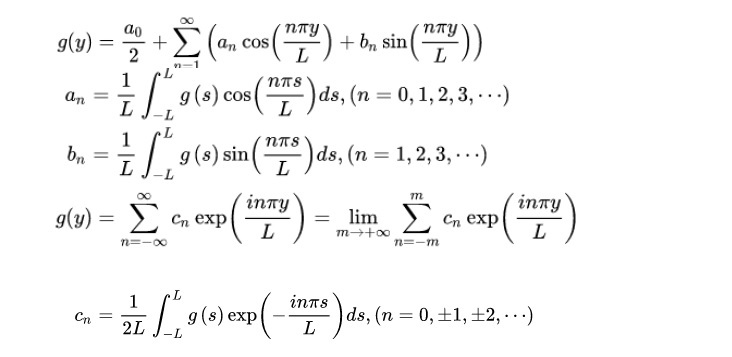

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




