- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-
コラム
2021年04月02日
文字サイズ
- 小
- 中
- 大
はじめに
大分以前になってしまったが、以前の研究員の眼「「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-」(2020.9.8)で、「三角関数」の定義について、紹介した。また、研究員の眼「数学記号の由来について(7)-三角関数(sin、cos、tan等)-」(2020.10.9)では、三角関数の記号(sin、cos、tan等)の由来について紹介した。
今回と次回の研究員の眼では、「三角関数の性質」として、高校時代に学んだいくつかの公式や定理等について、その有用性を含めて、紹介したいと思う。
「三角関数」と言われると、つい学生時代に試験問題で悩まされたことを思い出して、嫌悪感を抱いてしまう人も多いと思われるが、この時に学んだ各種の公式や定理がどんな意味を有していて、どのように有用なのかを知ることで、少しはこうした苦手意識を緩和して、三角関数を見直していただければと思っている。
今回と次回の研究員の眼では、「三角関数の性質」として、高校時代に学んだいくつかの公式や定理等について、その有用性を含めて、紹介したいと思う。
「三角関数」と言われると、つい学生時代に試験問題で悩まされたことを思い出して、嫌悪感を抱いてしまう人も多いと思われるが、この時に学んだ各種の公式や定理がどんな意味を有していて、どのように有用なのかを知ることで、少しはこうした苦手意識を緩和して、三角関数を見直していただければと思っている。
ピタゴラスの定理
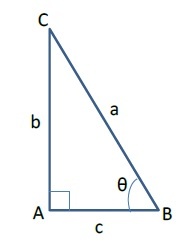
まずは、「ピタゴラスの定理」である。これは、多くの皆さんがご存じの通り、「直角三角形において、長辺の二乗の和が、他の2辺の二乗の和に等しい」というものである。算式で示せば、「直角三角形の3辺の長さをa(長辺)、b、cとした時に、a2=b2+c2 が成り立つ」というものである。
これから、以下の「ピタゴラスの基本三角関数公式」が成り立つことがわかる。

これから、以下の「ピタゴラスの基本三角関数公式」が成り立つことがわかる。

従って、また以下の算式が成り立つことになる。

このように、sin、cos、tan というのは、互いに独立なものではない。角度θが決まっていれば、もちろんsin、cos、tanを算出することができるが、一方でθの値が不明でも、sin、cos、tanのどれか1つの値が定まると、他の値も上記の算式等を用いて求めることができることになる。
この「ピタゴラスの定理」は、ギリシアの数学者のターレスが三角比を用いてピラミッドの高さを測定したように、建物の高さを測定する時に利用される。

このように、sin、cos、tan というのは、互いに独立なものではない。角度θが決まっていれば、もちろんsin、cos、tanを算出することができるが、一方でθの値が不明でも、sin、cos、tanのどれか1つの値が定まると、他の値も上記の算式等を用いて求めることができることになる。
この「ピタゴラスの定理」は、ギリシアの数学者のターレスが三角比を用いてピラミッドの高さを測定したように、建物の高さを測定する時に利用される。
即ち、これは「三角形の2辺の長さとその2辺で形成される角度が与えられた時に、残りの辺の長さを求める」ものとなる。「余弦」というのは、「cos(cosine)」のことを言うが、上記の算式でわかるようにcos(余弦)が主たる役割を果たしていることから、「余弦定理」と呼ばれている。
これは、いわゆる「ピタゴラスの定理」を一般化したものとなっている。即ち、「余弦定理」における特殊なケースが「ピタゴラスの定理」ということになる。つまり、「ピタゴラスの定理」は、直角三角形のケースの定理であるが。「余弦定理」は一般の三角形のケースに当てはまる定理ということになる。
これは、いわゆる「ピタゴラスの定理」を一般化したものとなっている。即ち、「余弦定理」における特殊なケースが「ピタゴラスの定理」ということになる。つまり、「ピタゴラスの定理」は、直角三角形のケースの定理であるが。「余弦定理」は一般の三角形のケースに当てはまる定理ということになる。
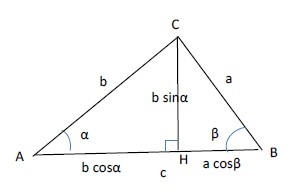
「余弦定理」は、例えば、以下のように証明される。
なお、「余弦定理」と呼ばれているものには、「第一余弦定理」と「第二余弦定理」があり、通常「余弦定理」と呼ばれている上記の定理は、このうちの「第二余弦定理」のことを指している。
因みに「第一余弦定理」は、以下のものであり、「三角形の2辺とそれらに対峙する角の角度がわかっているときに、もう 1 辺の長さが決まる」というものである。

これが正しいことは、例えば三番目の式については、上記の「第二余弦定理」の証明のプロセスで使用した図をみていただければお分かりいただけるものと思われる。
この「余弦定理」は、例えば、途中に障害物がある場合の2つの地点AとBの間の距離を測定する場合に、別の地点Cを選定して、AC及びBC間の距離と∠ACBの角度を測定することで、AB間の距離を求める場合に利用できる。
因みに「第一余弦定理」は、以下のものであり、「三角形の2辺とそれらに対峙する角の角度がわかっているときに、もう 1 辺の長さが決まる」というものである。

これが正しいことは、例えば三番目の式については、上記の「第二余弦定理」の証明のプロセスで使用した図をみていただければお分かりいただけるものと思われる。
この「余弦定理」は、例えば、途中に障害物がある場合の2つの地点AとBの間の距離を測定する場合に、別の地点Cを選定して、AC及びBC間の距離と∠ACBの角度を測定することで、AB間の距離を求める場合に利用できる。
正弦定理
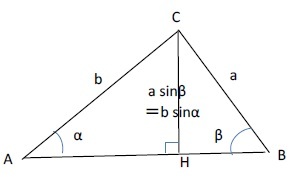
「正弦定理」と言われるものは、「三角形の3辺の長さをa、b、c、それぞれの辺に対向する角度をα、β、γとした時に、以下の算式が成り立つ」というものである。「正弦」とはsin(sine)のことを言うが、以下の算式でわかるようにsins(正弦)が主たる役割を果たしていることから、「正弦定理」と呼ばれている。

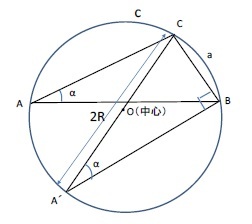
これは、「三角形の1辺の長さとその両端の2つの角度から、他の2辺の長さを求める」ものである。さらに、この三角形の外接円1の半径をRとすると、以下の算式が成り立つ。


これは、「三角形の1辺の長さとその両端の2つの角度から、他の2辺の長さを求める」ものである。さらに、この三角形の外接円1の半径をRとすると、以下の算式が成り立つ。

この「正弦定理」は、いわゆる「三角測量」と呼ばれるものに利用される。
「三角測量」は、ある基線の両端にある既知の点から測定したい点への角度をそれぞれ測定することによって、その点の位置を決定する測量方法である3。
対象物までの距離が、例えば極めて遠くにある等の理由で、測定できない場合でも、角度は対象物を見ることができれば測定できる。そのため、広範囲の地域をカバーでき、大規模測量に適している。
例えば、月等の天体までの距離についても、地球上の2地点において観測される緯度の差異から求めることができることになる。
「三角測量」は、ある基線の両端にある既知の点から測定したい点への角度をそれぞれ測定することによって、その点の位置を決定する測量方法である3。
対象物までの距離が、例えば極めて遠くにある等の理由で、測定できない場合でも、角度は対象物を見ることができれば測定できる。そのため、広範囲の地域をカバーでき、大規模測量に適している。
例えば、月等の天体までの距離についても、地球上の2地点において観測される緯度の差異から求めることができることになる。
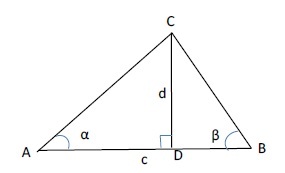 右図において、測定対象となるCまでの距離dは、2地点AB間の距離cとA、Bにおける角度α、βを用いて、以下のように表される。
右図において、測定対象となるCまでの距離dは、2地点AB間の距離cとA、Bにおける角度α、βを用いて、以下のように表される。d=c×sinα・sinβ/sin(α+β)
{証明}
c=AD+DB=d/tanα+d/tanβ=d(cosα/sinα+cosβ/sinβ)
=d(sinα・cosβ+cosα・sinβ)/sinα・sinβ
ここで、次回の研究員の眼で説明する加法定理により、
sin(α+β)= sinα・cosβ+cosα・sinβ であるから、上式が得られる。
三角測量は、1980年代に衛星測位システムが登場するまで、大規模精密測量に用いられてきた。
1 全ての三角形には、外接円(3つの頂点と接する円)が存在する。
2 「円周角の定理」は、(1)1つの弧に対する円周角は等しい、(2)その円周角はその弧に対する中心角の半分に等しい、というものである。円周上の2点A、Bを円周上の点Cと結ぶことによって形成されるのが「円周角」であり、中心Oと結ぶことによって形成されるのが「中心角」である。従って、弧ABが半円(線分ABが中心Oを通る場合、円周角は90°となる(「ターレスの定理」)。
3 これに対して、「三辺測量」は、三角網と呼ばれる非常に大きな三角形群の各辺の距離を正確に測ることにより、三角点の位置を正確に求めるものである。
(2021年04月02日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
| 2025/09/12 | 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月14日
ロシアの物価状況(25年9月)-低下が続くが、足もとインフレ圧力の強まりも -
2025年10月14日
今週のレポート・コラムまとめ【10/7-10/10発行分】 -
2025年10月10日
企業物価指数2025年9月~国内企業物価の上昇率は前年比2.7%、先行きは鈍化予想~ -
2025年10月10日
中期経済見通し(2025~2035年度) -
2025年10月10日
保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-のレポート Topへ



















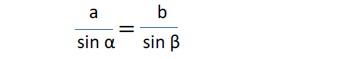
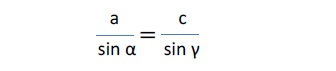
 が得られる。
が得られる。

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




