- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その2)-加法定理、二倍角、三倍角、半角の公式等-
コラム
2021年05月06日
文字サイズ
- 小
- 中
- 大
はじめに
これまで、三角関数については、研究員の眼「「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-」(2020.9.8)で、「三角関数」の定義について、研究員の眼「数学記号の由来について(7)-三角関数(sin、cos、tan等)-」(2020.10.9)では、三角関数の記号(sin、cos、tan等)の由来について紹介した。さらに、前回の研究員の眼では、高校時代に学んだいくつかの公式や定理等のうち、「余弦定理」、「正弦定理」、「正接定理」等について紹介した。
今回の研究員の眼では、三角関数の「加法定理」、「二倍角、三倍角、半角の公式」、「合成公式」、「和と積の変換公式」等について、その有用性を含めて紹介したい。
今回の研究員の眼では、三角関数の「加法定理」、「二倍角、三倍角、半角の公式」、「合成公式」、「和と積の変換公式」等について、その有用性を含めて紹介したい。
加法定理
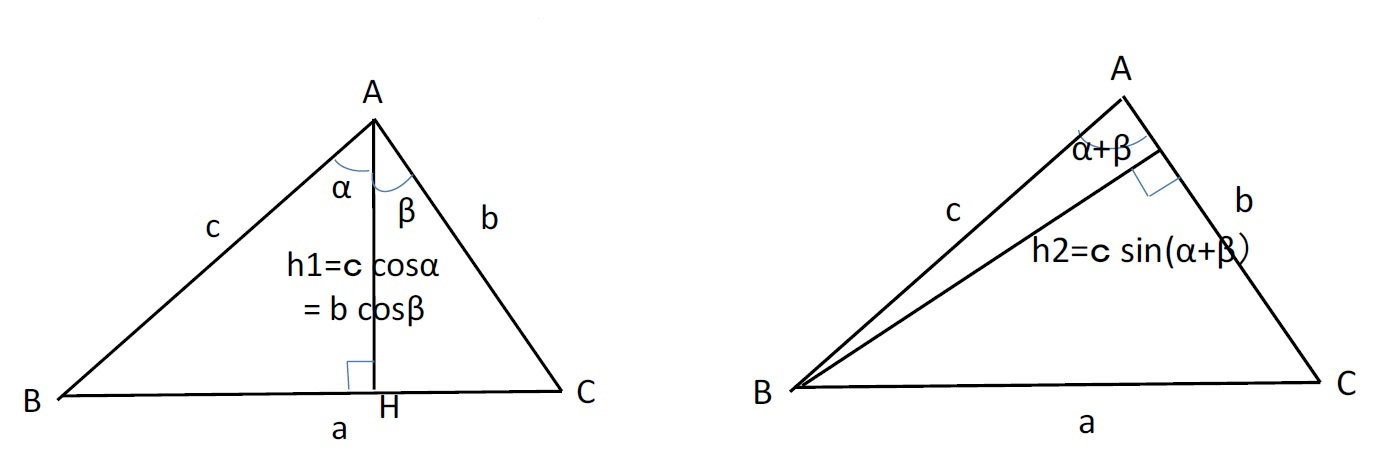
この「加法定理」の証明には、いくつかの方法があるが、ここでは3つの方法の概略を示しておく(以下の証明で示している図等におけるαやβに関しては、代表的なケースを想定したものとなっているので、必ずしも一般性はないことには注意が必要である)。
[証明1]単位円周上の2点間の距離の公式と余弦定理を利用する方法
右図のように、単位円周上に、2点、P(cosα、sinα)、Q(cosβ、sinβ)をとる。
[証明1]単位円周上の2点間の距離の公式と余弦定理を利用する方法
右図のように、単位円周上に、2点、P(cosα、sinα)、Q(cosβ、sinβ)をとる。
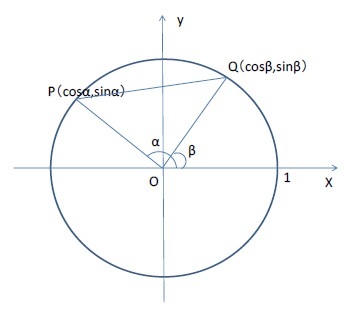 距離の公式から、
距離の公式から、PQ2=(cosβ―cosα)2+ (sinβ―sinα)2
=(cos2α+sin2α)+(cos2β+sin2β)
―2(cosα・cosβ+sinα・sinβ)
=2-2(cosα・cosβ+sinα・sinβ)
一方で、△POQに(前回の研究員の眼で説明した)余弦定理を適用して、
PQ2=OP2+OQ2-2OP・OQ・cos∠POQ
=2-2cos(α―β)
上記の2つの式から
2-2(cosα・cosβ+sinα・sinβ)=2-2cos(α―β)
∴cos(α―β)=cosα・cosβ+sinα・sinβ
[証明3]オイラーの公式(Euler's formula)を利用する方法
オイラーの公式 eiθ=cosθ+i sinθ を用いると
ei(α+β)=cos(α+β)+i sin(α+β)
一方で、
ei(α+β)= eiα・eiβ
=(cosα+i sinα)・(cosβ+i sinβ)
= cosα・cosβ-sinα・sinβ+i(sinα・cosβ+cosα・sinβ)
∴ sin(α+β)=sinα・cosβ+cosα・sinβ
cos(α+β)=cosα・cosβ-sinα・sinβ
なお、加法定理を発見したのは、ギリシアの天文学者であるプトレマイオス(Claudius Ptolemaeus, 83年頃 - 168年頃)であると言われている。
彼は、「円に内接する四角形ABCDにおいて、AC×BD=AB×CD+BC×AD という等式が成り立つ」という「トレミー(Ptolemy)の定理」(プトレマイオスの英語名がトレミー)を発見し、加法定理と本質的に同じ結論を導いている。
「トレミーの定理」は、例えば余弦定理を用いて、以下のように証明できる。
オイラーの公式 eiθ=cosθ+i sinθ を用いると
ei(α+β)=cos(α+β)+i sin(α+β)
一方で、
ei(α+β)= eiα・eiβ
=(cosα+i sinα)・(cosβ+i sinβ)
= cosα・cosβ-sinα・sinβ+i(sinα・cosβ+cosα・sinβ)
∴ sin(α+β)=sinα・cosβ+cosα・sinβ
cos(α+β)=cosα・cosβ-sinα・sinβ
なお、加法定理を発見したのは、ギリシアの天文学者であるプトレマイオス(Claudius Ptolemaeus, 83年頃 - 168年頃)であると言われている。
彼は、「円に内接する四角形ABCDにおいて、AC×BD=AB×CD+BC×AD という等式が成り立つ」という「トレミー(Ptolemy)の定理」(プトレマイオスの英語名がトレミー)を発見し、加法定理と本質的に同じ結論を導いている。
「トレミーの定理」は、例えば余弦定理を用いて、以下のように証明できる。
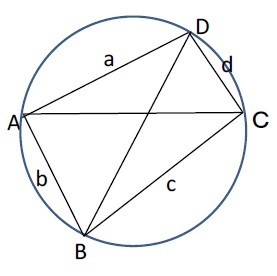 〔トレミーの定理の証明〕
〔トレミーの定理の証明〕右図において、△ABD及び△BCDに余弦定理を適用して
BD2=a2+b2-2ab cos∠A=c2+d2-2cd cos∠C
ここで、円に内接する四角形の性質より、∠C+∠A=π であることから、cos∠C=-cos∠Aとなり、
BD2=a2+b2-2ab cos∠A=c2+d2+2cd cos∠A
上記の両辺の式からcos∠Aを消去して、整理すると以下の通りとなる。
(ab+cd)BD2=(a2+b2)cd+(c2+d2)ab=(ad+bc)(ac+bd)
ACについても、同様にして、
(ad+bc)AC2=(ab+cd)(ac+bd)
両式を掛け合わせて、
(ab+cd)(ad+bc)AC2・BD2=(ab+cd)(ac+bd)(ad+bc)(ac+bd)
これを整理して、平方根をとれば、
AC・BD=ab+cd
となることが示される。
この「トレミーの定理」を用いて、加法定理を以下のように証明できる。
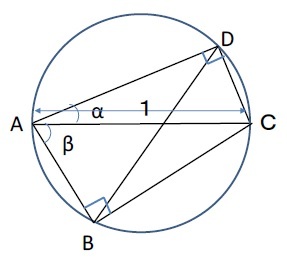
[証明4]トレミーの定理と正弦定理を利用する方法
右図のようなACを直径1とし、∠DAC=α、∠CAB=βとなる四角形ABCDを考えると、
合成公式
この合成公式を用いることにより、「sinとcosの定数倍の和」という扱いにくい関数をsinやcosという1つの関数のみで表すことができることになる。これにより、例えば関数の最大値や最小値等の算出が容易になって、扱いやすいものとなる。
和と積の変換公式
一般的には、掛け算よりも加減算の方が計算が簡単なため、計算機の無い時代においては、sin、cos、tan等の三角比の表等から値を求めるために、積和公式は有用なものだった。
加法定理や和と積の変換公式等の利用
今回述べてきた各種の定理や公式は、どのように利用されるのであろうか。
まずは、〔証明1〕の単位円の図が示しているように、角度αに角度βを足すことは、単位円上で角度βだけ「回転」させることに相当している。この考え方を利用すると、各種のゲームのプログラミングやCG(コンピュータ・グラフィックス)、人工衛星の軌道計算、さらにはアート作品等の様々な分野で活用することができることになる。
さらには、次回説明する三角関数の「波」との関係に基づくと、「積和公式」を用いることで、2つの(周波数を有する)波を表す三角関数を掛け合わせることで、別の2つの(周波数を有する)波を形成することができることになる。このようにして(例えば、自らが適切に処理でき、必要とする)周波数を有する波への変換を行うことができることになる。
まずは、〔証明1〕の単位円の図が示しているように、角度αに角度βを足すことは、単位円上で角度βだけ「回転」させることに相当している。この考え方を利用すると、各種のゲームのプログラミングやCG(コンピュータ・グラフィックス)、人工衛星の軌道計算、さらにはアート作品等の様々な分野で活用することができることになる。
さらには、次回説明する三角関数の「波」との関係に基づくと、「積和公式」を用いることで、2つの(周波数を有する)波を表す三角関数を掛け合わせることで、別の2つの(周波数を有する)波を形成することができることになる。このようにして(例えば、自らが適切に処理でき、必要とする)周波数を有する波への変換を行うことができることになる。
まとめ
以上、今回は「三角関数の性質」として、高校時代に学んだいくつかの公式や定理等のうち、「加法定理」、「二倍角、三倍角、半角の公式」、「合成公式」、「和と積の変換公式」等について、その有用性を含めて紹介した。
「加法定理や和と積の変換公式等の利用」で述べたように、今回説明してきた加法定理や積和公式等の各種の定理や公式は、「三角関数」と「波」との関係において、波の表現への利用等を通じて、大きく役に立っている。これらについては、次回以降の研究員の眼で説明していくこととしたい。
「加法定理や和と積の変換公式等の利用」で述べたように、今回説明してきた加法定理や積和公式等の各種の定理や公式は、「三角関数」と「波」との関係において、波の表現への利用等を通じて、大きく役に立っている。これらについては、次回以降の研究員の眼で説明していくこととしたい。
(2021年05月06日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月21日
選択と責任──消費社会の二重構造(2)-欲望について考える(3) -
2025年10月21日
連立協議から選挙のあり方を思う-選挙と同時に大規模な公的世論調査の実施を -
2025年10月21日
インバウンド消費の動向(2025年7-9月期)-量から質へ、消費構造の転換期 -
2025年10月21日
中国、社会保険料徴収をとりまく課題【アジア・新興国】中国保険市場の最新動向(71) -
2025年10月21日
今週のレポート・コラムまとめ【10/14-10/20発行分】
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「三角関数」の基本的な定理とその有用性を再確認してみませんか(その2)-加法定理、二倍角、三倍角、半角の公式等-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「三角関数」の基本的な定理とその有用性を再確認してみませんか(その2)-加法定理、二倍角、三倍角、半角の公式等-のレポート Topへ





















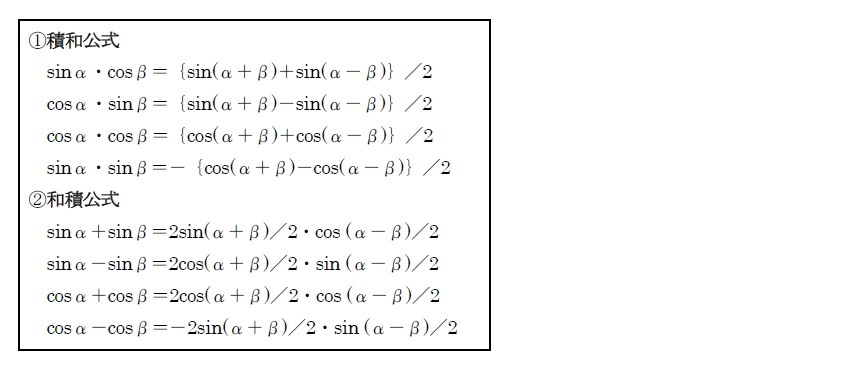



 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




