「三角関数」と「波」の関係－三角関数による「波」の表現と各種の波（電磁波、音波、地震波等）

はじめに

これまで、三角関数については、研究員の眼「「三角関数」って、何でしたっけ？－sin(サイン)、cos(コサイン)、tan(タンジェント)－」（2020.9.8）で、「三角関数」の定義について、研究員の眼「数学記号の由来について（7）－三角関数（sin、cos、tan等）－」(2020.10.9)では、三角関数の記号（sin、cos、tan等）の由来について紹介した。さらに、前回と前々回の研究員の眼では、高校時代に学んだいくつかの公式や定理等のうち、「余弦定理」、「正弦定理」、「正接定理」、「加法定理」、「二倍角、三倍角、半角の公式」、「合成公式」、「和と積の変換公式」等について、その主として「測量」の世界等における有用性を含めて紹介した。

今回の研究員の眼では「三角関数」の社会での応用として、最も幅広い関りがある「波」との関係について触れてみたい。

「三角関数」のグラフ

三角関数の定理や公式は覚えていなくても、三角関数のグラフについては、記憶の片隅に残っていて、こんなものだったよなという認識を有しておられる方が多いのではないかと思われる。

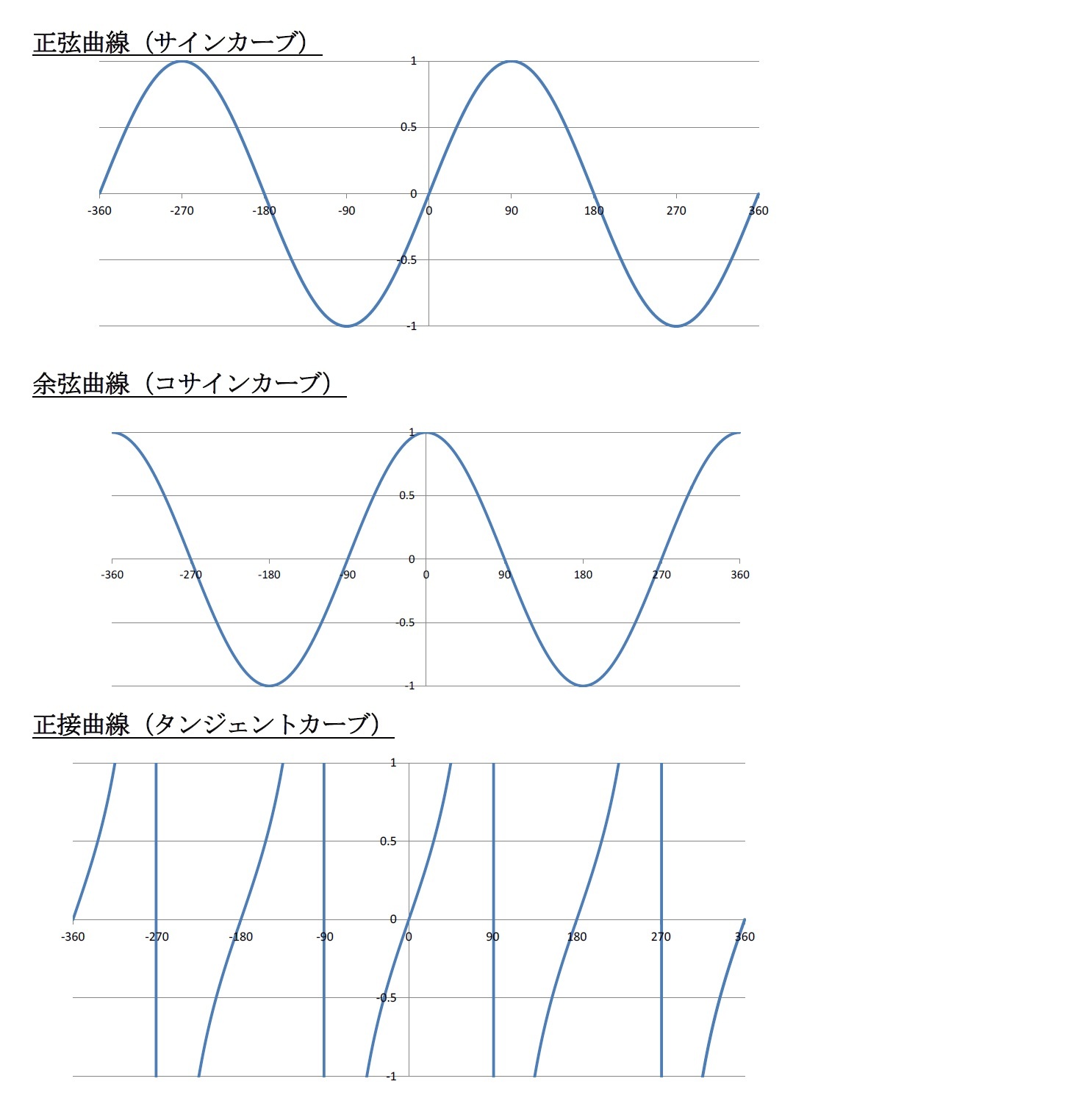
横軸（x）に角度を、縦軸（y）にsin（サイン）やcos（コサイン）やtan（タンジェント）の値を表すグラフを描くと、次ページのような「波」を表す曲線になっている。それぞれの曲線が、「サインカーブ（正弦曲線）」、「コサインカーブ（余弦曲線）」、「タンジェントカーブ（正接曲線）」と呼ばれる。

これらのグラフから以下のことがわかる。

(1) それぞれの曲線は、一定の間隔で同じ形を繰り返す。これを「周期」と呼んでいる。「正弦曲線」と「余弦曲線」の周期は2π（ラジアン）（360°）、「正接曲線」の周期はπ（180°）となる。

(2) 「正弦曲線」や「正接曲線」は、原点に対して対称なグラフになっている（いわゆる「奇関数」）。

(3) 「余弦曲線」は、縦軸（y）に対して対称なグラフになっている（いわゆる「偶関数」）。

(4) 「余弦曲線」と「正弦曲線」はπ／２（90°）だけずれた同じ曲線である。

(5) 「正接曲線」は、奇関数で、直線（n＋1／2）πを漸近線に持っている。

正弦曲線（サインカーブ）/余弦曲線（コサインカーブ）/正接曲線（タンジェントカーブ）

「波」について

「波」あるいは「波動」、英語で「wave」と呼ばれるものは、同じようなパターンが空間を伝播する現象のことをいう。物理学における「波動」は、何らかの物理量の空間分布パターンが伝播する現象を指している。

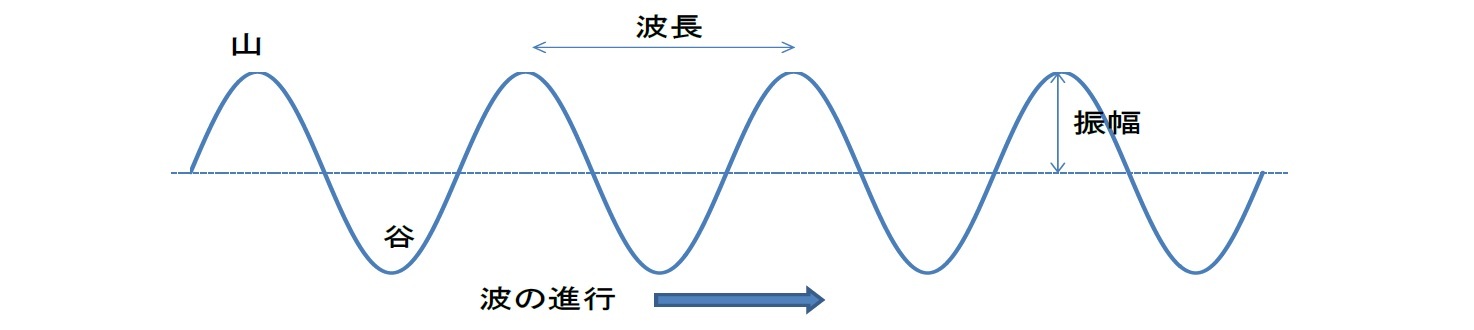
また、「波動」は、空間的な広がりをもつ「振動（oscillation、vibration）」であると解釈することができ、波動と振動は相互作用することが多いとされている。周期性のある振動において、単位時間あたりの振動の数を「振動数（又は周波数）」（単位はHz（ヘルツ））、振動のふれ幅を「振幅」、振動の一単位にかかる時間を「周期」という。「周期」は「周波数」の逆数である。また、「波動」における山（最も高い場所）から次の山までの長さを「波長」と呼んでいる。これらが「波」の基本要素となっている。また、この時、波の「速度」は、「振動数×波長」で示されることになる。

主な「波」としては、「電磁波」（「光波」、「電波」）、「音波」、「地震波」、「重力波」、「津波」等が挙げられる。

電磁波
「電磁波（electromagnetic wave）」は、電場と磁場の変化を伝搬する波であり、電子〈電荷〉の振動によって発生する。電場と磁場とも、波の進行方向に対して直交し、しかも互いに垂直な方向に振動する「横波」である。

電磁波と呼ばれるものは、その波長によって、以下のように分類される。波長が長いものから、いわゆる「電波（波長0.1mm程度以上）」と呼ばれるものから、「赤外線」、「可視光」、「紫外線」（以上の３つが「光波（波長が1 mm から 2 nm 程度）」と呼ばれる）、「X線（波長が 10 nm 以下）」、「ガンマ線（波長が 10 pm 以下）」となっている。

なお、これらの分類の境界は統一的に定められたものではなく、学問分野・国ごとの法律・規格等によって多少の違いがある。

波長が長いほど、広がりながら進みやすく、進行方向に多少の障害物があっても進行することができることになる。一方で、波長が短いほど、（広がらずに）直進性が高くなる。また、波長が短い波ほど、そのエネルギーが高くなる。

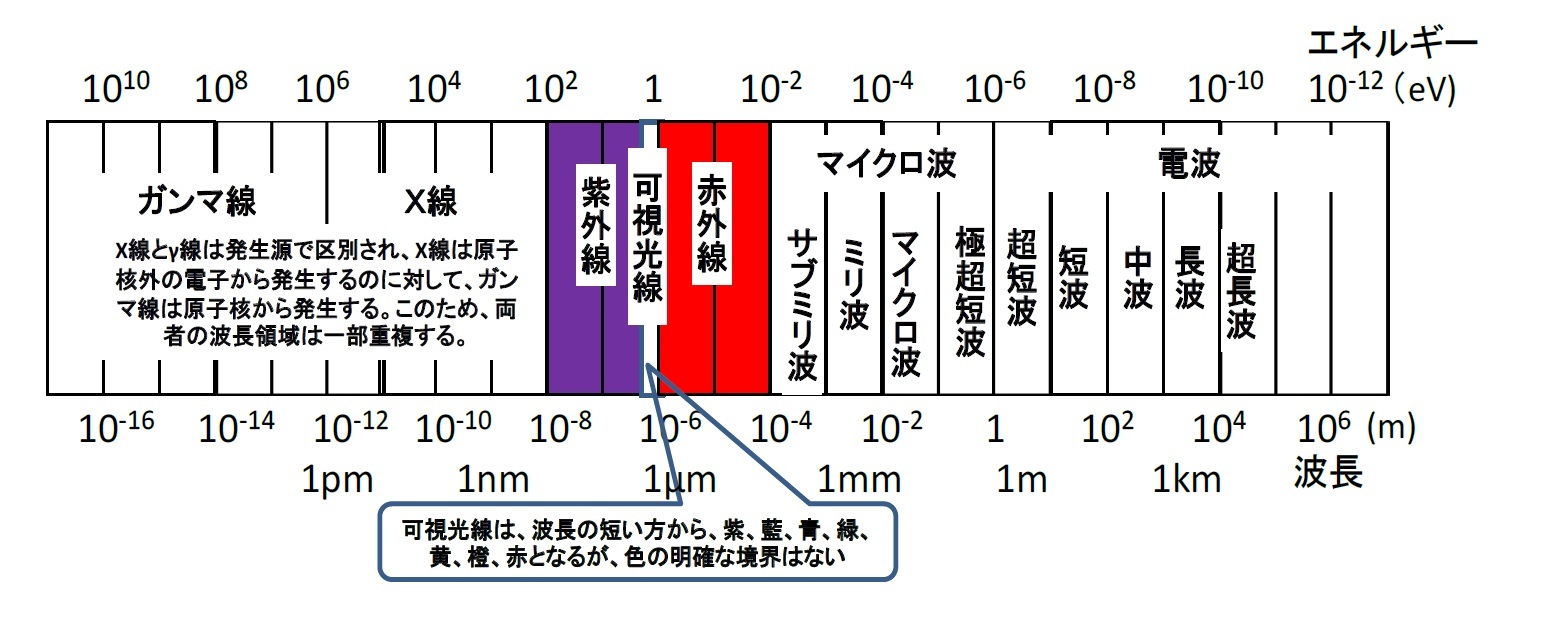
結果として、波長が長い「電波」は、通信や放送に利用される。その中でも、「マイクロ波」とよばれるものが、無線LANや衛星放送等、「極超短波」は、携帯電話、テレビ（UHF放送、地上デジタル放送）等、「超短波」は、ラジオ（FM放送）、テレビ（VHF放送）等、「短波」は、ラジオ（短波放送）、船舶の無線等に、「中波」はラジオ（AM放送）や船舶の無線等にそれぞれ利用される。

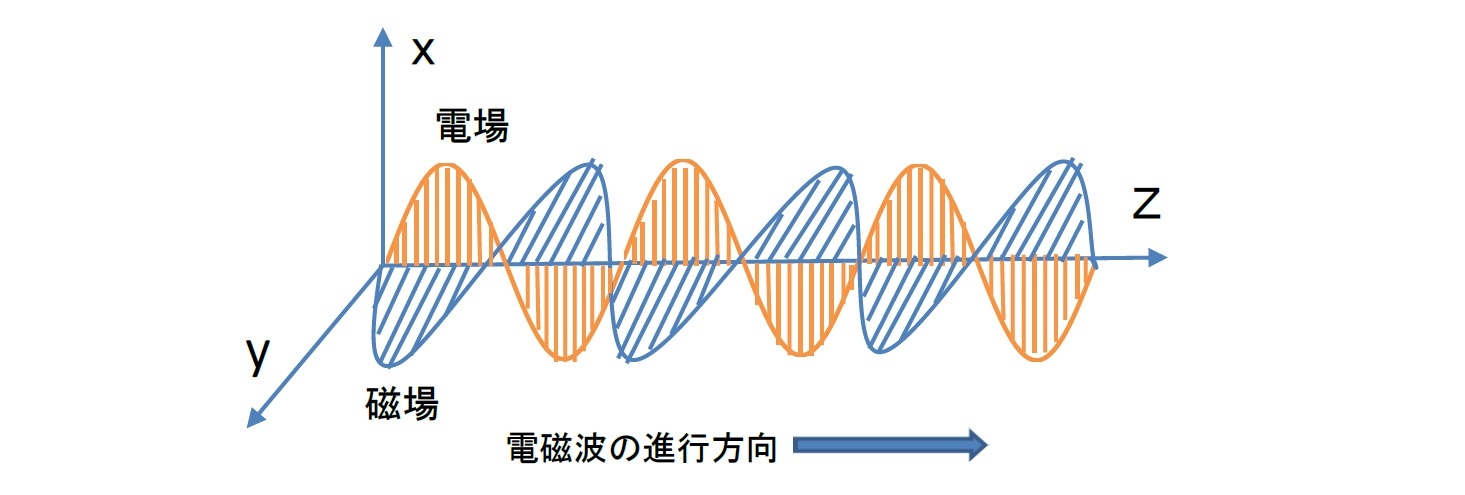
一方で、電波よりも波長が短い「光波」は、物質に吸収されて化学反応や発熱などの相互作用を生じることがある。「赤外線」は、物を温めることに利用され、暖房器具やサーモグラフィ等で利用される。「可視光線」が、まさに人間の眼の網膜を刺激することで、視覚を与えてくれている。また、「紫外線」は、エネルギーが高いため、皮膚に当たると日焼けを起こすことになる。前ページの図表からわかるように、「可視光線」の波長域は全体の中では極めて限定された範囲（紫から赤まで約400nmから約800nmの2倍の範囲）に留まっている。

さらに、波長が短い「X線」になると、光子の持つエネルギーが大きいため、分子に吸収されて熱振動に変わることはなく、物質を構成する電子などに直接作用するため、比重の小さい物質ほどよく透過するようになる。このため、この現象を利用することで、レントゲン写真やX線CTの撮影ができることになる。一方で、「X線」や「ガンマ線」はエネルギーが大きいため、人間が大量に浴びると健康を害することになる。

音波
「音波（acoustic wave）」というのは、気体、液体、固体を問わず、弾性体を伝播するあらゆる弾性波の総称を指している。

狭義では、人間や動物の「可聴周波数」である空中を伝播する弾性波を指しており、人などの生物がこれを聴覚器官によって捉えると音として認識している。この狭義の意味での「音波」は、空気分子を互いに揺らして、空気の密度が疎と密な部分を発生させて、伝わっていく「縦波」となる。

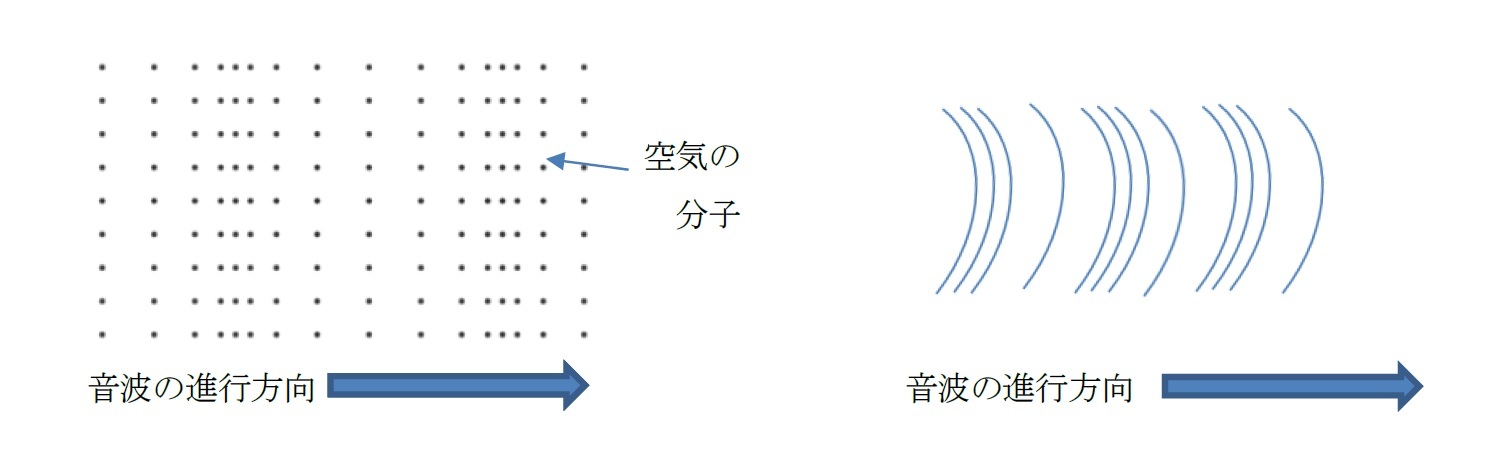
気体・液体中の音波は、媒質にずれ弾性が存在しないため疎密波として伝播する「縦波」であるが、固体中では疎密波のほかに横波であるせん断波（ねじれ波）も生じる。

なお、人間の可聴周波数は、20Hzから2万Hzと三桁に及んでおり、視覚に比べてその領域は幅広くなっている。可聴周波数より高い周波数の弾性波を「超音波」、低い周波数の弾性波を「超低周波」と呼ぶ。

音波の速度である「音速」は、媒質の密度と弾性率（一定量の変形を起こすのに必要な圧力）によって変化するが、一般的に気体、液体、固体の順に音速は早くなっていく。

なお、周期の長短（周波数の高低）は「音の高さ」に相当しており、周期が長い（周波数が低い）と音は低く、周期が短い（周波数が高い）と高く聞こえる。また、振幅が大きいほど音は大きくなる。

地震波
「地震波（seismic wave、earthquake wave）は、文字通り、地震により発生する波のことを言う。

「地震波」は大きくは、「実体波（body wave）」と呼ばれる、媒体内部で粗密やたわみなどの変位が（岩盤等を）伝播していくもの、と「表面波（surface wave）」と呼ばれる、固体や気体や液体の境界（地球の表面等）を伝わる波に区分される。

有名な「P波」や「S波」と呼ばれるものは、実体波である。
　
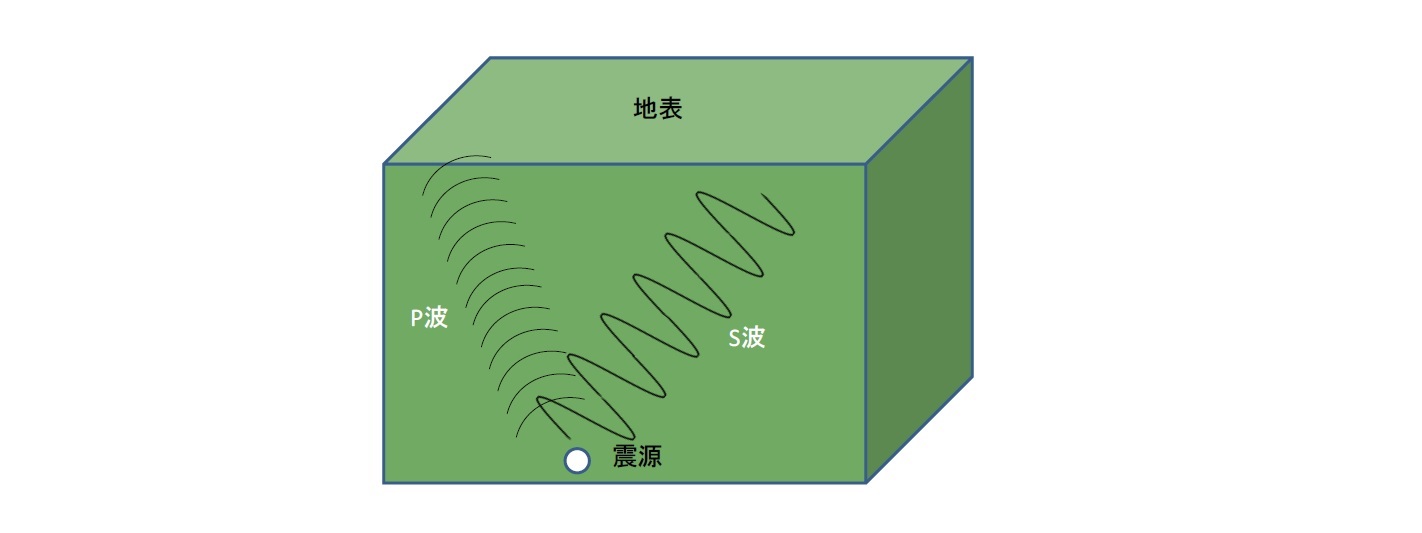
「P波」は、Primary wave（第一波）の略で、進行方向に平行に振動する弾性波で、いわゆる「縦波」であり、固体・液体・気体を伝わる。P波は速度が速く、地震発生時最初に到達する地震波で、初期微動を起こす。

「S波」は、Secondary wave（第二波）の略で、進行方向と直角に振動する弾性波で、いわゆる「横波」であり、固体を伝わる。P波に続いて到達し、主要動と呼ばれる大きな揺れを起こす。被害をもたらすのは主にS波である。

なお、P波（縦波）、S波（横波）というのは、あくまでも進行方向に対しての縦横であり、P波で建物が上下に揺れる（縦揺れ）、あるいはS波で建物が左右に揺れる（横揺れ）とは限らない。

また、表面波は、S波よりもさらに速度が遅くなる。