- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- フィボナッチ数列について(その1)-フィボナッチ数列とはどのようなものでどんな性質を有しているのか-
文字サイズ
- 小
- 中
- 大
はじめに
フィボナッチ数列とは
F0 = 0
F1 = 1
Fn+2 = Fn + Fn+1 (n ≥ 0) 〈※〉
これによれば、最初の数列は、以下の通りとなる。
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, …
イタリアの数学者レオナルド・フィボナッチ(Leonardo Fibonacci)(本名はレオナルド・ピサノ(Leonardo Pisano)1というが、父の名前のボナッチの息子という意味のfilius Bonacciが短縮されてフィボナッチと呼ばれるようになった)に因んで名付けられた数列である。
フィボナッチは、1202年のその著書『算盤の書』で、アラビア数字の位取り記数法等のシステムを欧州に導入したことで有名であるが、一方でこの著書の中で、以下に述べる兎(うさぎ)の問題で、いわゆる「フィボナッチ数列」の考え方を西洋で初めて紹介したことで、その名を歴史に大きく残すことになった。
1 イタリアの都市ピサは「ピサの斜塔」で有名であるが、12世紀から13世紀にかけては商業都市の中心的存在だった。
兎の問題
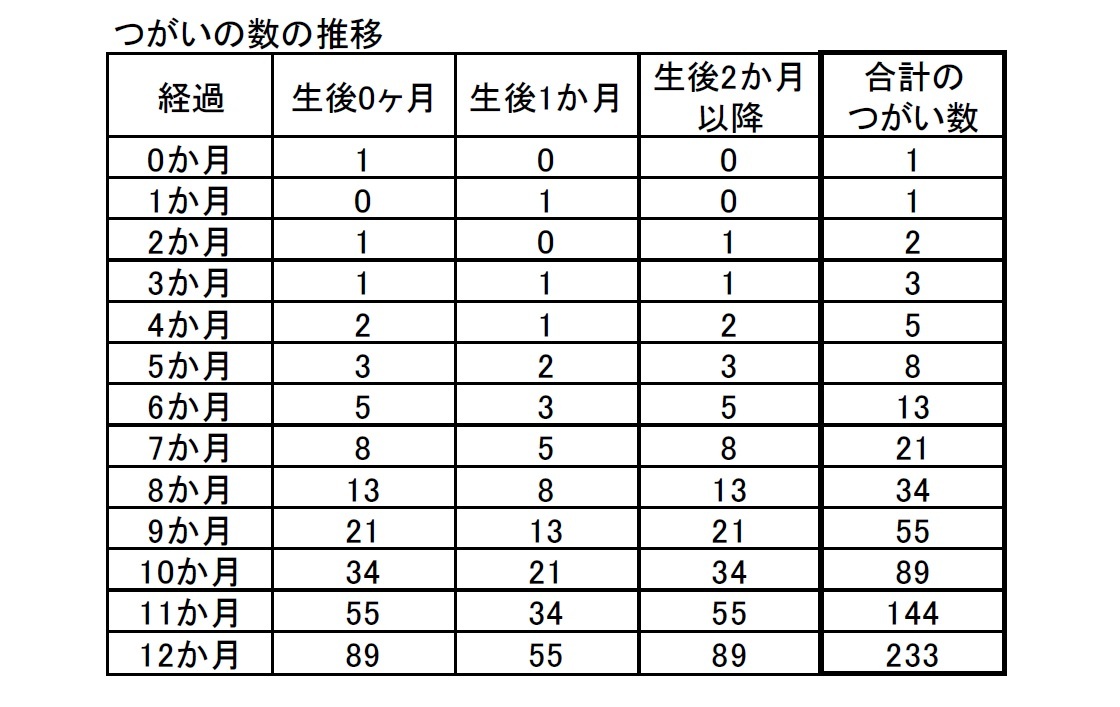
・1つがいの兎は、生後2か月後から毎月1つがいの兎を産み、兎が死ぬことはないものとする。この場合に、産まれたばかりの1つがいの兎は1年後に何つがいの兎になるか?
これによると、つがい数の推移は以下の表のようになる。どの月の合計のつがい数も、その前の2つの月の合計のつがい数の和となり、フィボナッチ数が現れてくる。
なお、このオリジナルのフィボナッチの問題では、F0=1、F1 = 1、F2 =2 となるため、先に述べた現在の一般的なフィボナッチ数列のケースとは、初期値が異なっていることになる。ただし、初期値が異なっていても、以下で述べるようなフィボナッチ数列の性質は変わらない。
一般項
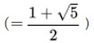 を用いて、次の式で表される。これをフランスの数学者ジャック・フィリップ・マリー・ビネ(Jacques Philippe Marie Binet)に因んで「ビネの公式(Binet's formula)」という。不思議に思われるかもしれないが、式の中に無理数の
を用いて、次の式で表される。これをフランスの数学者ジャック・フィリップ・マリー・ビネ(Jacques Philippe Marie Binet)に因んで「ビネの公式(Binet's formula)」という。不思議に思われるかもしれないが、式の中に無理数の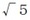 が含まれているが、結果数値は常に自然数になる。
が含まれているが、結果数値は常に自然数になる。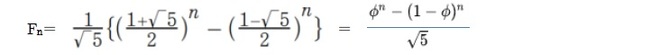
なお、|1-φ|<1であることから、上式における第2項はnが大きくなると0に近づいていくことになるので、結局Fnは第1項を整数に丸めたものとなっていく。
また、φも1-φも方程式x2=x+1の解であることから、φnも(1-φ)nも、前述のフィボナッチの漸化式(※)を満たしていることになる。従って、任意の整数aとbに対して、
aφn + b(1-φ)nもフィボナッチの漸化式を満たすことになる。
一般項を表す「ビネの公式」の証明
フィボナッチ数列の性質
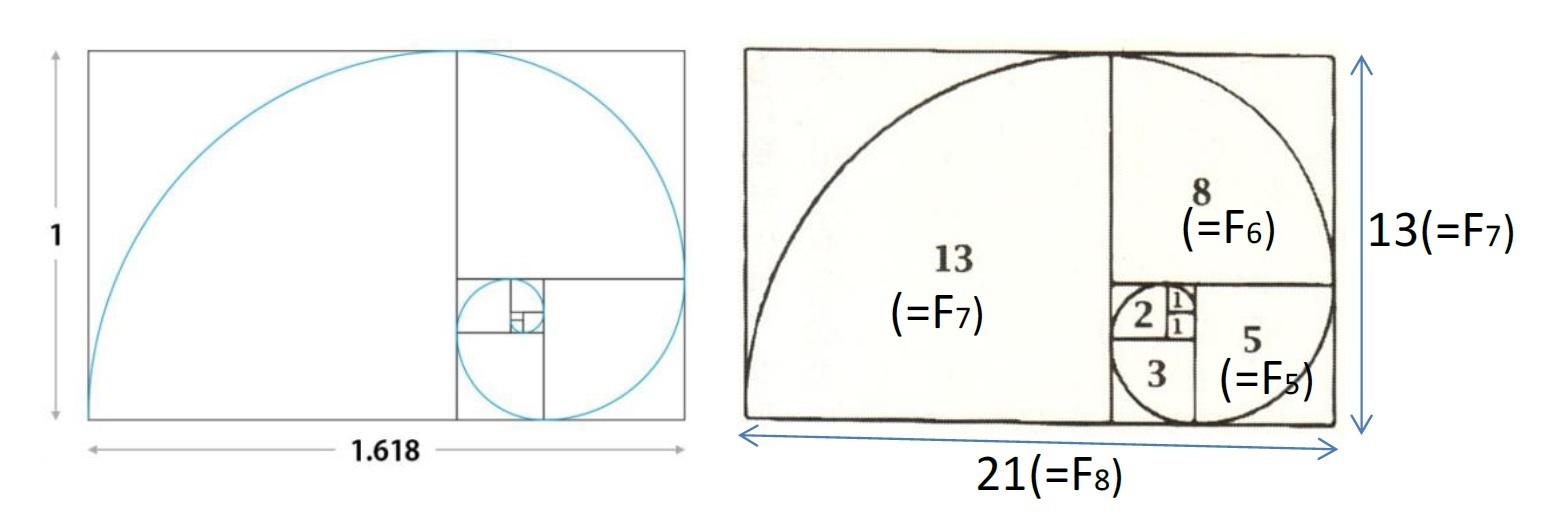
(その1)(初期値 (F0 = 0, F1 = 1) に依らずに)フィボナッチ数列の隣接2項の商は黄金数 φ に収束する。
これについては、研究員の眼「黄金比φについて(その1)-黄金比とはどのようなものなのか-」(2020.11.10)で述べた。
(その2)自然数 p, q の最大公約数を r とすると、Fp と Fq の最大公約数は Fr となる。
この性質の特殊なケースとして、連続する2つの数は互いに素であることより、「連続するフィボナッチ数は互いに素である。」といえる。
FnとFn-1が共通の約数p≥2を有するとすると、Fn=mp、Fn-1=np と書けることになることから、その漸化式より、
Fn-2=Fn-Fn-1=(m-n)p
となり、Fn-1とFn-2も共通の約数pを有することになる。
これを繰り返していくと、結局F1とF2も共通の約数pを有することになり、これは明らかに矛盾する。
(その3)フィボナッチ数の累和や累積等については、多くの関係式が成立している。そのうちのいくつかの例を挙げると、例えば以下の式が成り立つ。
(1) F1 + F2 + F3 + … + Fn = Fn+2 − 1
(2) F1 + F3 + F5 + … + F2n−1 = F2n 又は F3 + F5 + … + F2n−1 = F2n-1
(3) F2 + F4 + F6 + … + F2n = F2n+1 − 1
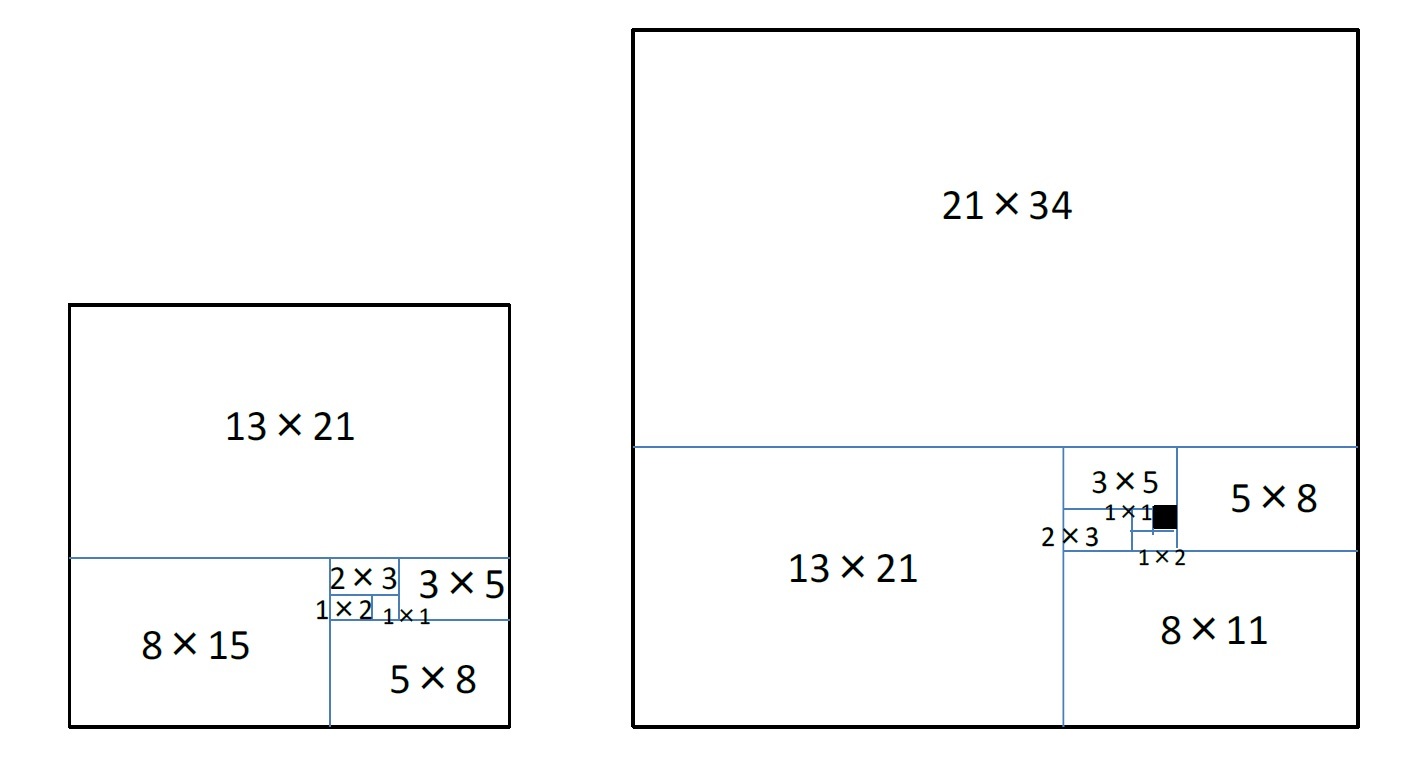
(4) F12 + F22 + F32 + … + Fn2 = Fn Fn+1
(1)は、(2)と(3)が証明されれば、2つを足した結果として明らかなので、(2)を証明すると
F2n=F2n-1+F2n-2=F2n-1+F2n-3+F2n-4=・・・
=F2n-1+F2n-3+・・・+F5+F3+F2=F2n-1+F2n-3+・・・+F5+F3+F1
同様にして、(3)についても、以下のように証明される。
F2n⁺1=F2n+F2n1-=F2n+F2n-2+F2n-3=・・・
=F2n+F2n-2+・・・+F4+F2+F1=F2n+F2n-2+・・・+F4+F2+1
(4)については、帰納法で証明できる。
n=1 の時は、F12=1、F1F2=1 となるので成り立つ。
nの時に成り立つとすると、(4)の両辺にFn+12 を加えて
F12 + F22 + F32 + … + Fn2+Fn+12 = Fn Fn+1 +Fn+12
= Fn+1(Fn+1 +Fn+1)=Fn+1Fn+2
となって、n+1でも成り立つ。
(その4)任意の正の整数は、1つ以上の連続しない相異なるフィボナッチ数の和として一意に表現できる(これは、ベルギーの数学者エドゥアール・ゼッケンドルフ(Edouard Zeckendorf) に由来して、「ゼッケンドルフの定理」と呼ばれる)。
まずは、「任意の正の整数は、1つ以上の連続しない相異なるフィボナッチ数の和として表現できる」ことを帰納法で示す。
n=1の時は、明らか
nまで成立するとして、(n+1)以下の最大のフィボナッチ数をFkとする。
(n+1)-Fk=0の時は、n+1=Fk となることから、表現可能
(n+1)-Fk≠0の時は、n+1-Fkは表現可能なので、n+1=(n+1-Fk)+Fk も表現可能
さらに、n+1<Fk+1=Fk+Fk-1 より、n+1-Fk<Fk-1 となることから、上記のn+1表現にFkと連続するFk-1は使用されない。よって、n+1でも成り立つ。
次に、一意性を示す。
仮に、nに異なる2つの表現があるとした場合、双方に含まれるフィボナッチ数から共通するものを差し引いたものから、最大のフィボナッチ数をFkとする。この時、Fkを含まない表現は、全てFkより小さいフィボナッチ数の連続した和で表されていることになるので、上記の(その3)(2)及び(3)の性質(F1=F2からF1とF3は連続している)より、その総和はFk未満となってしまい、矛盾する。
ここで、F11=89 である。上記の関係式は、この1/F11 は、全てのフィボナッチ数を小数点以下一桁ずつずらして得られる数値の総和として表現されるということである。具体的には以下の通りである。
1/89=0.011235955⋯⋯⋯
=0.01+0.001+0.0002+0.00003+0.000005+0.0000008+0.00000013+0.000000021⋯⋯⋯
何とも不思議な関係であると思わないだろうか。
(その6)フィボナッチ数の逆数を全て足し合わせると収束する( André-Jeanninの定理)。
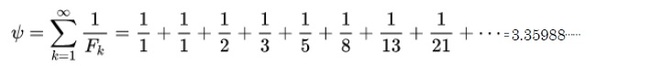
この収束値(逆フィボナッチ定数)は無理数である。
なお、フィボナッチ数列には、以下のような性質もある(さらに、一般化可能だがここでは特殊なケースだけを示している)。
フィボナッチ数列の一般化等
一般化されたフィボナッチ数列
フィボナッチ数列の初期値を以下のように一般化することができる。
G0 = p
G1 = q
Gn+2 = Gn + Gn+1 (n ≥ 0)
この時、以下の等式が成り立つ。
Gn+1 =p Fn + qFn+1 (n ≥ 0)
また、この「一般化されたフィボナッチ数列」の隣接2項の商も黄金比φに収束する。
リュカ数
この「一般化されたフィボナッチ数列」の特殊なケースとして、最初の2項を 2と1 に置き換えた数列(即ち、L0 = 2、L1 =1)の項を「リュカ数(ルカ数)」という。フランスの数学者エドゥアール・リュカ(Édouard Lucas)はフィボナッチ数列の数学的な意義を認めて、その名前を付けたと言われている2。
リュカ数の最初の数列は、以下の通りとなる。
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, …
この数列の一般項は、以下のように表される。
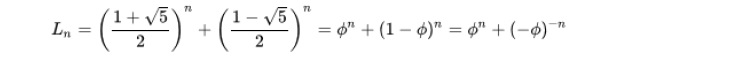
リュカ数についても、いくつかの面白い性質がある。例えば、(ここでは証明しないが)「pが素数であるとき、Lp-1はpで割り切れる」ということが挙げられる。具体的にはL7=29であるが、L7-1=28は7で割り切れるというような具合である。
2 フィボナッチ数列の一般化である「リュカ数列」という概念があるがここでは触れない。
「トリボナッチ数」3は、直前の三項の和として各項が定まる数列である。具体的には、以下の漸化式による。
T0 = T1 = 0
T2 = 1
Tn+3 = Tn + Tn+1 + Tn+2 (n ≥ 0)
と表される。最初の数列の値は次の通りとなる。
0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, …
トリボナッチ数の隣接する2項の比も一定の値(トリボナッチ定数1.839286…)に収束していくが、この値も無理数で、3次方程式 x3-x2-x-1=0 の実数根となっている。
この形での一般化は、さらには、テトラナッチ数、ペンタナッチ数等といった形で行われていくことになる。
3 「フィボナッチ」はあくまでも人の名前であり、「フィ」に「2」という意味があるわけではないが、その一般化された数列は、「トリ(tri)(3)」や「テトラ(tetra)(4)」を使用した名称となっている。
なお、フィボナッチ数列は、漸化式 Fn = Fn−1 + Fn−2 を全ての整数 n に対して適用することにより、n が負の整数の場合に拡張できる。この場合 F−n = (−1)n+1Fn となる。
黄金螺旋
(その3)の(4)式が成り立つことは、以下の右図のn=7のケースを考えてもらうと、確認できる。
最後に
フィボナッチ数列については、その名前や存在自体はご存知の方も多いと思われるが、それが非常に面白い性質等を有していることがおわかりいただけたのではないかと思われる。それだからこそ、自然界やそれ以外の一般社会等においても、フィボナッチ数が幅広く現れたり、使用されたりしている。これについては次回以降にご紹介していきたい。
本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2021年01月26日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
ユーロ圏消費者物価(25年10月)-2%目標に沿った推移が継続 -
2025年11月04日
米国個人年金販売額は2025年上半期も過去最高記録を更新-但し保有残高純増は別の課題- -
2025年11月04日
パワーカップル世帯の動向(2)家庭と働き方~DINKS・子育て・ポスト子育て、制度と夫婦協働が支える -
2025年11月04日
「ブルー寄付」という選択肢-個人の寄付が果たす、資金流入の突破口 -
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【フィボナッチ数列について(その1)-フィボナッチ数列とはどのようなものでどんな性質を有しているのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
フィボナッチ数列について(その1)-フィボナッチ数列とはどのようなものでどんな性質を有しているのか-のレポート Topへ















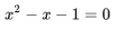
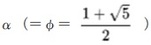
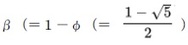
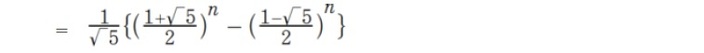


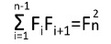
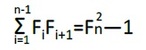

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




