コラム
2020年10月27日

「ハムサンドイッチの定理」って、知っていますか

このレポートの関連カテゴリ

Xでシェアする Facebookでシェアする

文字サイズ

  • 小
  • 中
  • 大
全文ダウンロード（PDF）

はじめに

数学の世界には、なかなか面白いネーミングを有する定理や法則等があることについては、過去の研究員の眼でいくつか紹介してきた。

今回は、「ハムサンドイッチの定理」について紹介したい。

「ハムサンドイッチの定理」とは？

「ハムサンドイッチの定理（ham sandwich theorem）」は、「ストーン・テューキーの定理（Stone–Tukey theorem」とも呼ばれ、「n 次元空間内に与えられた n 個の可測な「物体」に対して、それぞれを一度に等分することが出来るような (n − 1) 次元超平面が存在する」という定理である。ここで「可測（measurable）」であるとか、「超平面（hyperplane）」とか聴き慣れない用語がでてくるが、何となくイメージは湧くのではないかと思われる。

いずれにしても、このままではよくわからないと思われるので、ここではその名の示す通り、ハムとサンドイッチを対象にイメージがしやすい3次元空間（n=3）の例で説明することとする。

この場合、「ハムサンドイッチの定理」は、「ハムと2枚のパンという３つの物体がある場合に、これらの全ての物体の量を半分にすることができるような切り方（これは、3次元の物体を2次元の平面で切断することに相当）が存在する」というものである。

「ハムサンドイッチの定理」の意味するところ

さて、「ハムサンドイッチの定理」の意味するところについて、若干補足的な説明をしておく。

まずは、この定理において、３つの物体（すなわち、ハムと2枚のパン）の位置関係については何らの制限もない、ということが挙げられる。即ち、通常我々が考えるように、上下の2枚のパンがほぼ同じサイズで、その間にハムが挟まれているという状況だけでなく、ハムや2枚のパンが（3次元空間の）どの位置に置かれていようが成立する。

また、３つの物体の形状や大きさはどのようなものであっても構わない。１つの物体とみなすことができるものであれば、角形、球形、その他名称が付けられないような複雑な形のものであっても当てはまる。

「ハムサンドイッチの定理」を巡る簡単な歴史

この定理を一般的なケースで限られた紙面で説明することは簡単ではなく、このコラムの主旨でもないので、興味関心のある方は専門書を参考にしていただくことにして、ここでは、この問題を巡る簡単な歴史を述べておく。

この問題自体は、極めてシンプルで理解しやすいものと思われるが、この問題が提起されたのは比較的最近である。

米国の数学者であるB W. A. Beyer とAndrew Zardeckiによる2004年の論文「The Early History of the Ham Sandwich Theorem（ハムサンドイッチの定理の初期の歴史）」によると、3つの物体を平面で二等分する場合についての最も初期の既知の論文は、1938年のポーランドの数学者ヒューゴ・シュタインハウス（Hugo Steinhaus）らによるものだとされている。この1938年の論文によると、問題の提起はヒューゴ・シュタインハウスらによって行われ、「ボルスーク・ウラムの定理（Borsuk–Ulam theorem）」と呼ばれる定理を使用することによって、その証明はポーランドの数学者ステファン・バナッハ（Stefan Banach）によって発見された、とされている。

「パンケーキの定理」

「ハムサンドイッチの定理」は、3次元空間の場合であるが、これを2次元空間で考える場合には、「パンケーキの定理」と呼ばれる。これは、「２つの平面図形は１つの直線で2等分できる」ことを意味している。

「パンケーキの定理」の証明

2次元の場合の「パンケーキの定理」については、「Robertson–Webb回転ナイフの手順」と呼ばれる手法を用いて、証明される。これは、以下の通りとなる。
 

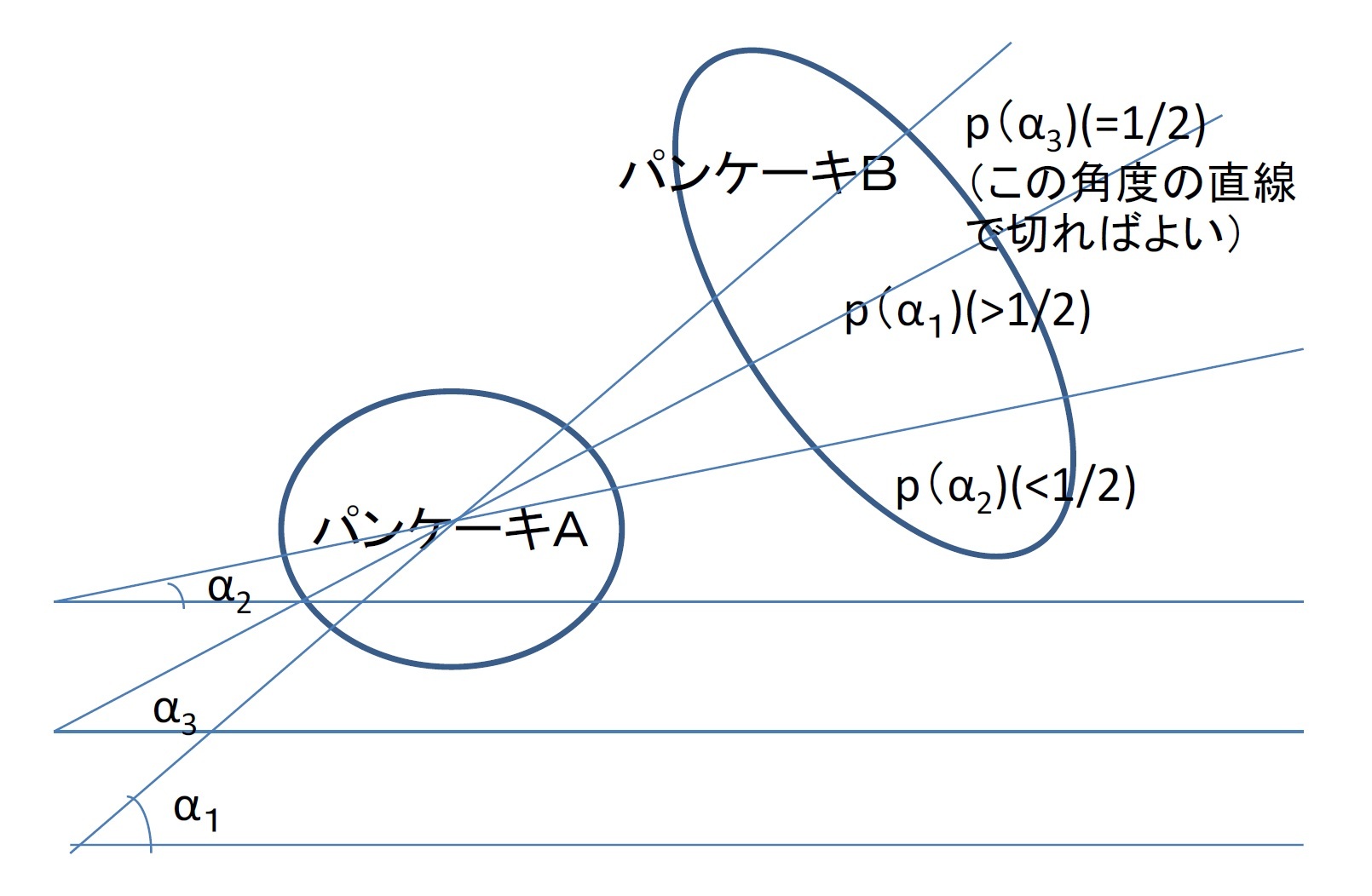
各角度α∈［0、180］について、角度αの直線を使用してパンケーキＡを2等分することができる（これは、角度αの直線を－∞から∞に移動することで、線でカバーされているパンケーキＡの割合が0から1まで連続的に変化するため、「中間値の定理」1では、途中のどこかで1/2に等しくなければならない、ことで確認される）。

これは、まっすぐなナイフを取り、それをあらゆる角度α∈［0、180］で回転させ、その特定の角度に合わせて適切に平行移動できることを意味している。これにより、パンケーキＡが各角度で2等分され、対応する平行移動が行われる。

ナイフの角度が0°の場合、パンケーキＢもカットされるが、これによって区分される２つのピースは通常等しくない（２つのピースが等しくなれば、これが求めるものとなる）。
ナイフの「ポジティブ」側を、パンケーキＢの割合が大きい側として定義する。 p（α）をナイフの「ポジティブ」側のパンケーキＢの割合、として定義すると、最初はp（0）≧ 1/2となる。

ナイフの角度が180°の場合、ナイフは逆さまになっているため、p（180）≦1/2となる。「中間値の定理」により、p(α)＝1/2となる角度がなければならない。その角度で切ると、両方のパンケーキが同時に２等分される。

上記の証明のイメージを図で示すと、以下の通りとなる。

角度α１、α２、α３　に対して、パンケーキAを2等分する直線が、下記のように示される。
「パンケーキの定理」の証明
 
1 実数直線 R の閉区間 I ＝［a, b］上で定義される連続な実数値関数 f が f(a) < f(b) を満たすとき、閉区間［f(a), f(b)］内の任意の点 γ に対して、γ ＝ f(c) となる I 内の点 c が存在する。

まとめ

以上、今回は数学における面白いネーミングを有する定理として、「ハムサンドイッチの定理」について紹介した。

これまでも述べてきているが、世の中には、それとなく注意して意識的に認識しないと、当たり前のこととして、あるいは何の考慮にも値しないこととして、気にも留めない事実が多いと思われる。さらには、そうした事実を気に留めたとしても、それはそうだろうな、正しいだろうな、とは思っても、それを証明せよと言われると、容易ではないケースが多い。

今回の「ハムサンドイッチの定理」もそのうちの１つであるように思える。名称は極めて身近なもので、その問題も誰でも理解できる。でも、どうやったら証明できるのだろうと思ってしまうだろう。

こうした問題を考えてみることで、数学に興味・関心を持っていただければと感じた次第である。

(2020年10月27日「研究員の眼」)

このレポートの関連カテゴリ

Xでシェアする Facebookでシェアする
全文ダウンロード（PDF）

中村 亮一

レポートについてお問い合わせ
(取材・講演依頼)

週間アクセスランキング

保険 総合 領域別

    更新もっと見る

    更新もっと見る

    ピックアップ

    レポート紹介

    【「ハムサンドイッチの定理」って、知っていますか】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。

    「ハムサンドイッチの定理」って、知っていますかのレポート　Topへ