コラム
2020年06月25日

「スリッパの法則」って、知っていますか

このレポートの関連カテゴリ

Xでシェアする Facebookでシェアする

文字サイズ

  • 小
  • 中
  • 大
全文ダウンロード（PDF）

はじめに

数学の世界には、なかなか面白いネーミングを有する用語があることについては、過去の研究員の眼でいくつか紹介してきた。

今回は、「スリッパの法則」及びそれに関連する話題について紹介したい。

投資の世界における「スリッパの法則」

「スリッパの法則」って言われて、ああ、あのことじゃないか、と思われる方々も少なからずいらっしゃるかもしれない。こうした方々は、おそらく「伝説のファンドマネジャー」と呼ばれるレオス・キャピタルワークス（「ひふみ投信」等で有名）代表取締役社長である藤野秀人氏の2004年の著書「スリッパの法則 - プロの投資家が教える「伸びる会社・ダメな会社」の見分け方」を思い出されるのではないかと思われる。

この著書によれば、「スリッパに履きかえる会社に投資しても儲からない」ということだそうで、スリッパに履き替えることに表れる「会社と家を同じようなものと考える悪しき家族主義」で、閉鎖的な会社となっていないか、という問題意識が背景にあるということのようだ。

数学の世界における「スリッパの法則」

ところが、今回紹介するのは、数学の世界における「スリッパの法則」である。

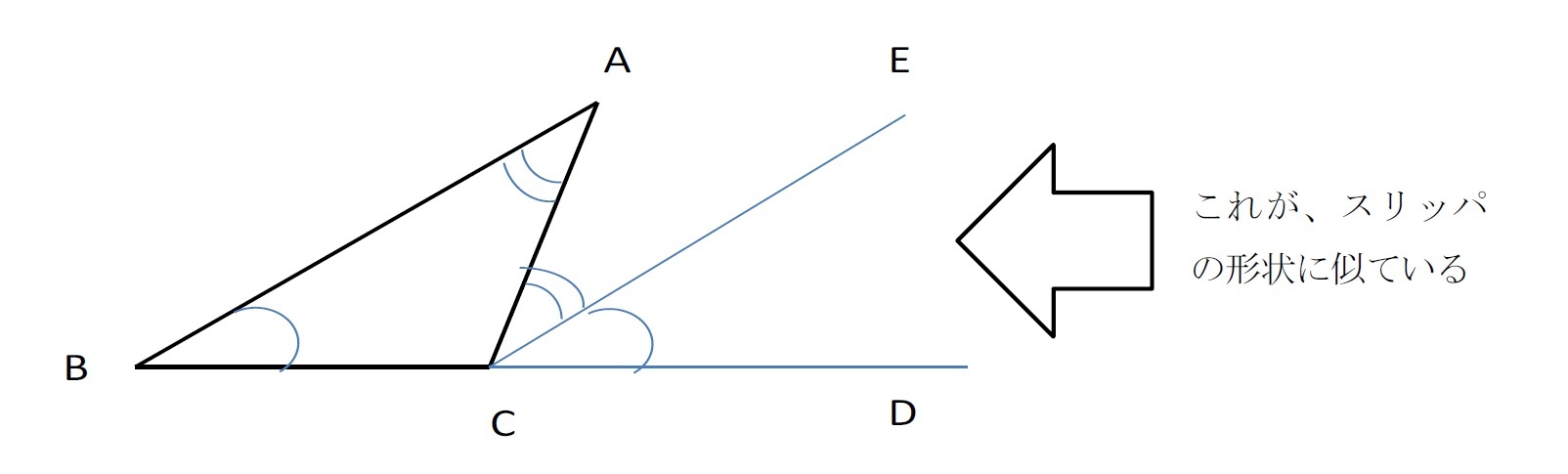
「スリッパの法則」は、本来的には「外角定理」と呼ばれているもので、「三角形において2つの内角の和は隣り合わない1つの外角と等しい」という定理である。これが「スリッパの法則」と呼ばれるのは、以下の図で示されるようなその形状に基づいている。

英語では「exterior angle theorem」と呼ばれるが、有名な「ユークリッド原論（Euclid's Elements）」に基づけば、「三角形の外角は、それと隣り合わない内角のいずれよりも大きい」というものがこれに相当することになる。これに対して、これから紹介する「スリッパの法則」と呼ばれるものは、学校で学ぶより一般的なものである。両者を区別するために、前者は「弱い形（weak form）」、後者は「強い形（Strong form）」と呼ばれることもあるようだ。前者の証明は、以下の「外角定理」の証明で使用される平行線公準（parallel postulate）1によっていないため、より基本的な結果となっている。
 
1 「ユークリッドの第5公準（公理）」とも呼ばれるもので、「1つの直線が2つの直線に交わり、その一方の側の内角の和が2直角（すなわち180°）より小さいならば、この2直線は限りなく延長されると、その2直角より小さい角のある側において交わる。」というものである。これを含めたユークリッドの公準が成立する幾何学が「ユークリッド幾何学」となる。

「外角定理」の証明

「外角定理」の証明は、通常、以下のように説明されると思われる。

下記の図のような三角形ABCを考える。
「外角定理」の証明
BCを延長した線CDとABと平行な線ECを引くと、

∠ABCと∠ECDは「同位角」となって等しいので、∠ABC＝∠ECD
∠BACと∠ACEは「錯角」となって等しいので、　∠BAC＝∠ACE

従って、

∠ACD（∠Cの外角）＝∠ACE＋∠ECD＝∠ABC＋∠BAC（∠Aと∠Bの内角）

となって、「外角定理」が証明されることになる。

ここで、「同位角」とか「錯角」という概念が出てくるが、平行線の性質から、これらが等しくなるということについては直感的には理解できると思われるので、これ以上は説明しない。

なお、このことはまた、「三角形の内角の和は180°に等しい」ということも示している。

「外角定理」の応用

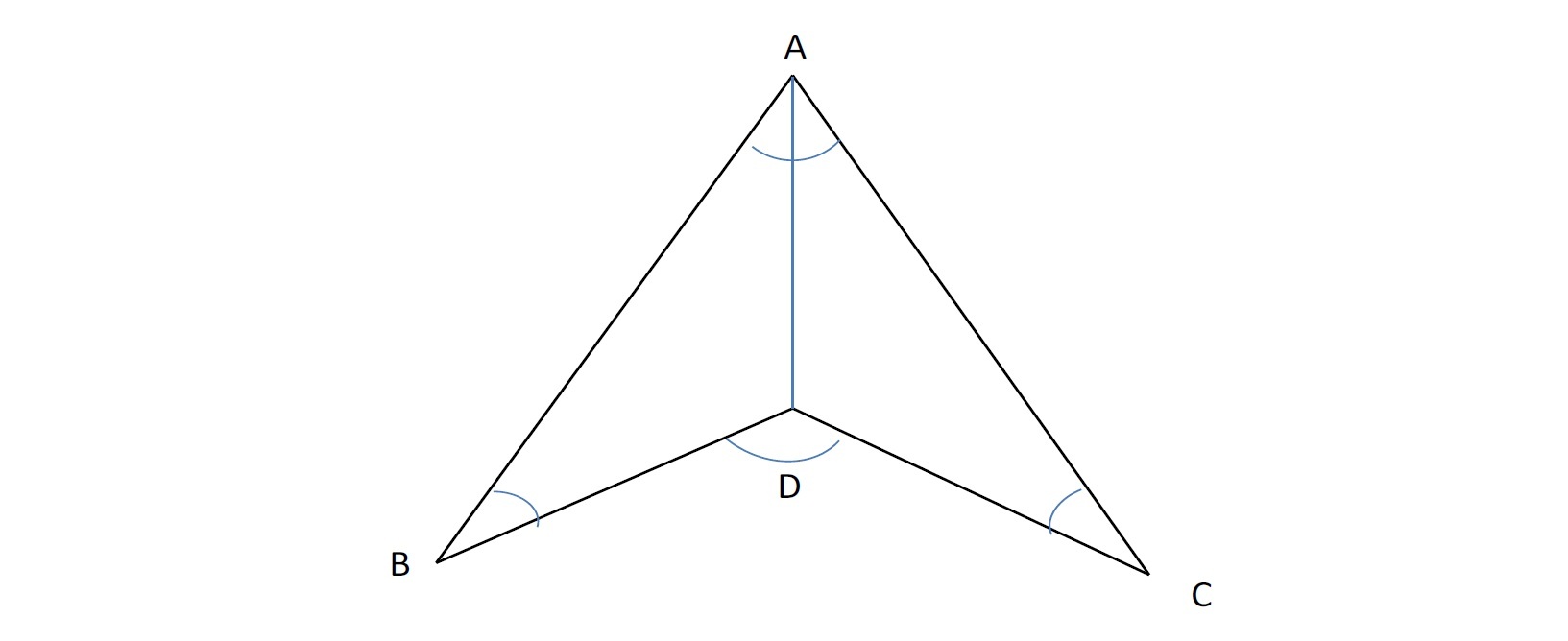
ブーメラン型の図形
以下のようなブーメラン型の図形ABDCでは、「∠A＋∠B＋∠C＝∠D」となる。

これは、ADの線を引いてみて、２つの三角形ABDとADCに分割し、２つの三角形に外角定理を適用すれば明らかである。
ブーメラン型
リボン型の図形
以下のようなリボン型の図形ABCDでは、「∠A＋∠B=∠C＋∠D」となる。

これも、三角形ABEと三角形ECDの外角定理を適用すれば明らかである。
リボン型
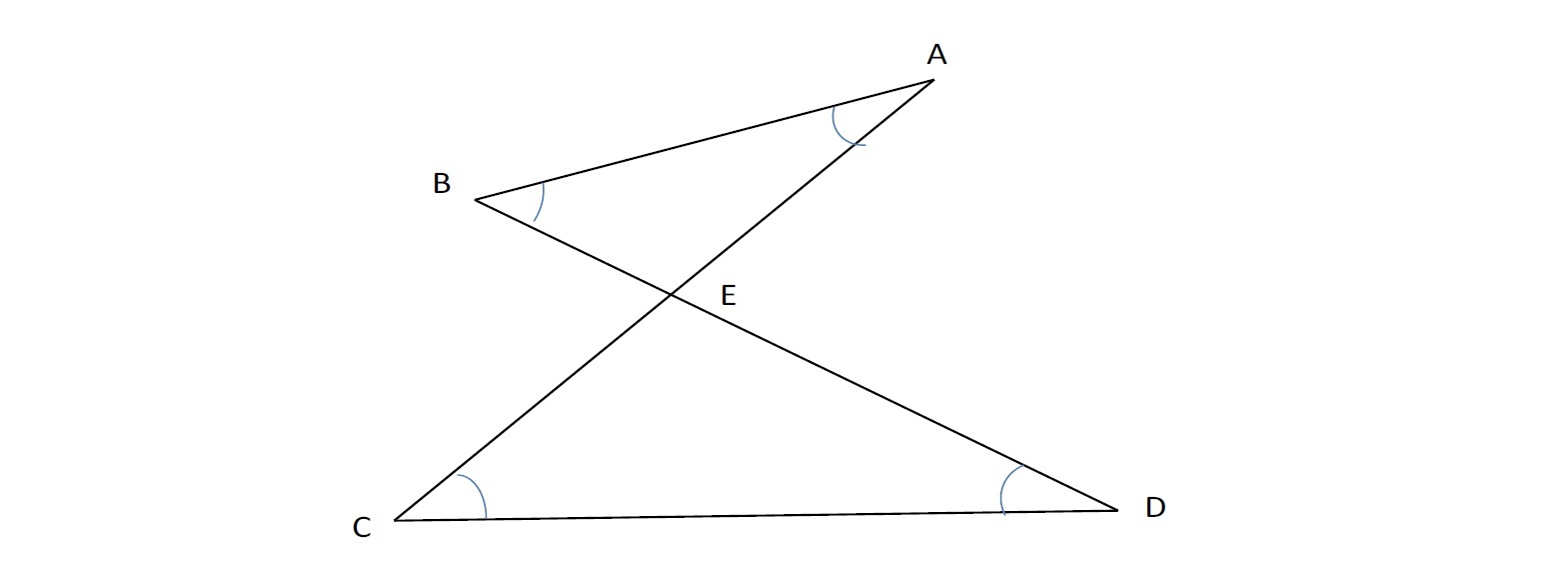
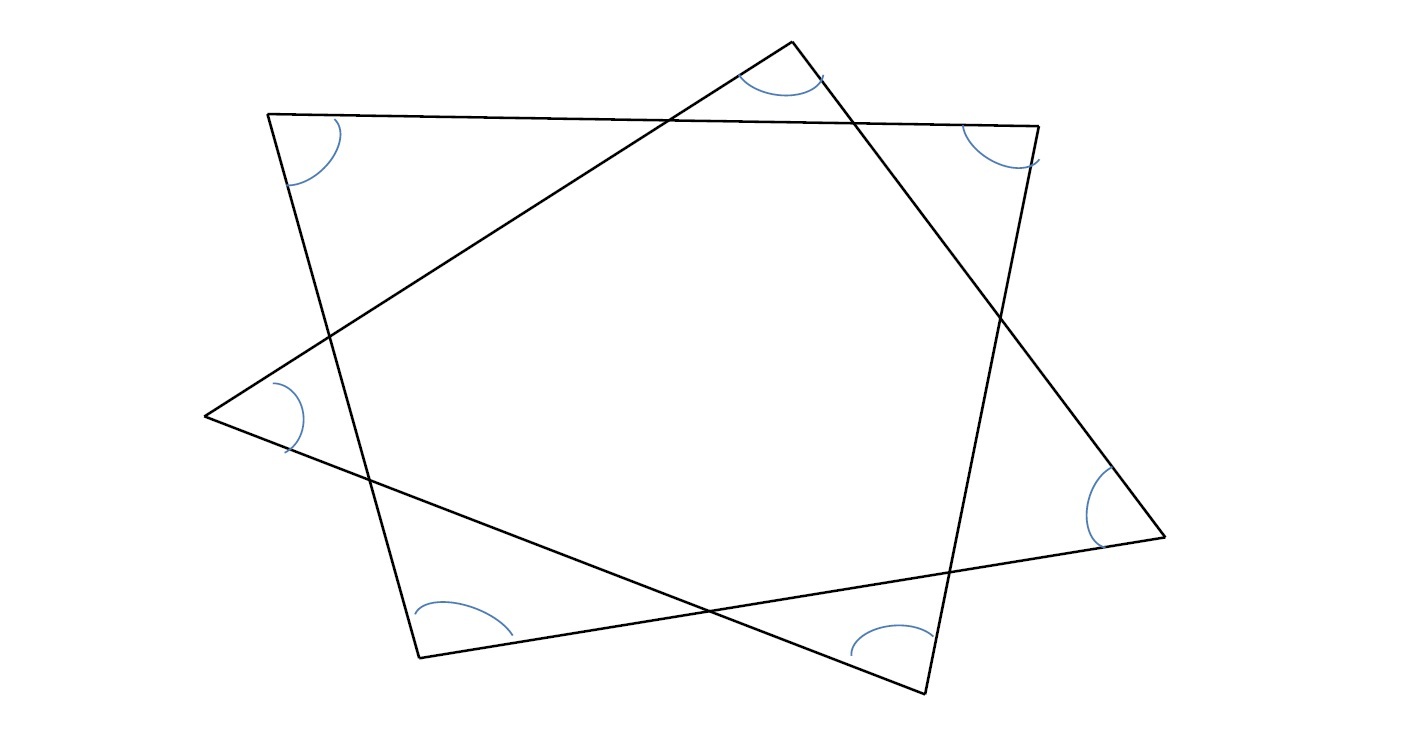
星型の多角形
以下のような星型の図形の場合の印しを付けた角度の合計を考える。
星型の多角形
この図形の場合、図形が示しているように、７つの三角形と１つの七角形に分割できる。

因みにn角形の内角の和は、ある１つの頂点をベースに（n－２）個の三角形に分割できることから、「180°×（nー２）」となり、これから逆算すれば、n角形の外角の和は「360°」となる。

従って、

180°×７（７つの三角形の内角の和）－360°×２（２つの外角の和）＝540°

となる。

この図形の場合、中に七角形が形成されているので、このような結果となるが、同じように７つの星があるような場合でも、別の星型では異なる結果となる場合もある。

いずれにしても、このように元の図形を三角形等の構成要素に分割し、外角定理等が適用できる形にしていくことで、解答が得られていくことになる。

まとめ

以上、今回は数学における「スリッパの法則（外角定理）」について紹介した。

最後は、中学校や高校の数学のおさらいのようになってしまったが、それでもあらためてこのようなことを知識として認識しておくと、何かの時に役に立つかもしれない。また、これを機会に図形に興味・関心を持つようになっていただければ幸甚である。
 
 

本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。

(2020年06月25日「研究員の眼」)

このレポートの関連カテゴリ

Xでシェアする Facebookでシェアする
全文ダウンロード（PDF）

中村 亮一

レポートについてお問い合わせ
(取材・講演依頼)

週間アクセスランキング

保険 総合 領域別

    更新もっと見る

    更新もっと見る

    ピックアップ

    お知らせ

    お知らせ一覧

    【「スリッパの法則」って、知っていますか】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。

    「スリッパの法則」って、知っていますかのレポート　Topへ