- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 複素数について(その2)-複素数と方程式-
コラム
2025年05月28日
文字サイズ
- 小
- 中
- 大
はじめに
今回の研究員の眼のシリーズでは、「虚数」及び虚数と実数で構成される「複素数」について、今一度それがどのようなもので、どんな性質を有しており、はたまたそれがどのように社会で役に立っているのか等について、何回かに分けて報告している。
まずは、前回は、「虚数」とは何か、から始めて、虚数と複素数の歴史と概要について、説明した。その歴史において説明したように、虚数や複素数の概念や研究が必要になってきたのは、方程式の解が実数の世界だけでは閉じておらず、虚数や複素数という新たな数字の概念が必要不可欠になってきたことによる。この虚数や複素数の研究を通じて、代数学の世界が飛躍的に進展していくことになる。
ということで、今回は複素数が数学の世界において、どのように有効に利用されているのかということで、方程式に関係するトピックについて説明する。
まずは、前回は、「虚数」とは何か、から始めて、虚数と複素数の歴史と概要について、説明した。その歴史において説明したように、虚数や複素数の概念や研究が必要になってきたのは、方程式の解が実数の世界だけでは閉じておらず、虚数や複素数という新たな数字の概念が必要不可欠になってきたことによる。この虚数や複素数の研究を通じて、代数学の世界が飛躍的に進展していくことになる。
ということで、今回は複素数が数学の世界において、どのように有効に利用されているのかということで、方程式に関係するトピックについて説明する。
代数学の基本定理
前回の研究員の眼でも紹介したように、1799年に、ヨハン・カール・フリードリヒ・ガウス(Johann Carl Friedrich Gauß)は、「代数学の基本定理」の証明を行っている1。
「代数学の基本定理(fundamental theorem of algebra)」というのは、「次数が 1 以上の任意の複素係数の一変数多項式には複素根が存在する2。」(あるいは「複素係数の一変数代数方程式は複素数の範囲で必ず解をもつ。」)という定理である3。
これはまた、因数定理(factor theorem)(多項式の根から元の多項式を因数分解することができる)に基づき、
「複素係数の任意の 一変数n次多項式
「代数学の基本定理(fundamental theorem of algebra)」というのは、「次数が 1 以上の任意の複素係数の一変数多項式には複素根が存在する2。」(あるいは「複素係数の一変数代数方程式は複素数の範囲で必ず解をもつ。」)という定理である3。
これはまた、因数定理(factor theorem)(多項式の根から元の多項式を因数分解することができる)に基づき、
「複素係数の任意の 一変数n次多項式
という形に因数分解されることになる。
この定理の証明については、いくつか知られているが、ここでは説明しない。
1 この時のガウスの証明は完全ではなかったが、後年に3つの異なる証明を与えている。
2 多項式P(x)の根は、方程式P(x)=0の解である。
3 「根」と「解」については、一般的には、重根を区別する場合には「根」、区別しない場合には「解」が使用されている(多項式には「根」、方程式には「解」と使い分けているケースもある)ようである。
この定理の証明については、いくつか知られているが、ここでは説明しない。
1 この時のガウスの証明は完全ではなかったが、後年に3つの異なる証明を与えている。
2 多項式P(x)の根は、方程式P(x)=0の解である。
3 「根」と「解」については、一般的には、重根を区別する場合には「根」、区別しない場合には「解」が使用されている(多項式には「根」、方程式には「解」と使い分けているケースもある)ようである。
1のn乗根
で与えられることになる。
となる。ここで、ルートの中の値がマイナスとなる場合、その解は虚数となる(殆どの人にとって、この二次方程式の解の公式において、初めて虚数なるものに出会うことになる)。
この二次方程式の解については、判別式(discriminant)D=b2-4ac に基づいて、以下の通りとなる。
・D>0の時、異なる2個の実数解を持つ。
・D=0の時、実数の重解を持つ。
・D<0の時、異なる2つの(互いに共役な)虚数解を持つ。
さて、上記においては、方程式の係数は実数としていた。それでは、係数が虚数(実数ではない複素数)の場合の二次方程式の解の公式の取扱はどうなるのだろうか。
複素係数の二次方程式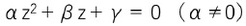 (α、β、γは複素数)を考える。代数学の基本定理により、この方程式にも2つの複素根が存在している。
(α、β、γは複素数)を考える。代数学の基本定理により、この方程式にも2つの複素根が存在している。
ところが、上記の解の公式をそのまま当てはめてしまうと、ルートの中に(実数係数の場合の実数とは異なり)虚数が現れてくることにもなる。
従って、この場合には、ルートの中の数字の状況によっては、上記の解の公式がそのままでは使用できないことになる。
ただし、この場合にも実数係数の二次方程式の解の公式を導き出すのと同様の考え方を適用していくことで、例えば以下の解の公式を導き出すことができる。
この二次方程式の解については、判別式(discriminant)D=b2-4ac に基づいて、以下の通りとなる。
・D>0の時、異なる2個の実数解を持つ。
・D=0の時、実数の重解を持つ。
・D<0の時、異なる2つの(互いに共役な)虚数解を持つ。
さて、上記においては、方程式の係数は実数としていた。それでは、係数が虚数(実数ではない複素数)の場合の二次方程式の解の公式の取扱はどうなるのだろうか。
複素係数の二次方程式
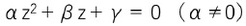 (α、β、γは複素数)を考える。代数学の基本定理により、この方程式にも2つの複素根が存在している。
(α、β、γは複素数)を考える。代数学の基本定理により、この方程式にも2つの複素根が存在している。ところが、上記の解の公式をそのまま当てはめてしまうと、ルートの中に(実数係数の場合の実数とは異なり)虚数が現れてくることにもなる。
従って、この場合には、ルートの中の数字の状況によっては、上記の解の公式がそのままでは使用できないことになる。
ただし、この場合にも実数係数の二次方程式の解の公式を導き出すのと同様の考え方を適用していくことで、例えば以下の解の公式を導き出すことができる。
ここで、Re(δ)はδの実数部、|δ|はδの絶対値(複素数δとその共役複素数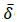 の積の平方根)で、δが実数であれば、これは通常の二次方程式の解の公式に一致することになる。
の積の平方根)で、δが実数であれば、これは通常の二次方程式の解の公式に一致することになる。
なお、二次方程式の解の公式の研究については、紀元前の古代ギリシアのユークリッド(Euclid)やそれ以前にまで遡るが、ゼロの概念が無かったことや、17世紀まで負の数が認められなかったため、負の数を回避する形式で制限的なものであった。7世紀のインドの数学者であるブラフマグプタ(Brahmagupta)は、その著書の中で二次方程式の解の公式を言葉で明示していた。
今日知られている形式での二次方程式の解の公式は、ルネ・デカルト(René Descartes)の1637年の著書『La Géométrie』(幾何学)において見られた。
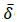 の積の平方根)で、δが実数であれば、これは通常の二次方程式の解の公式に一致することになる。
の積の平方根)で、δが実数であれば、これは通常の二次方程式の解の公式に一致することになる。なお、二次方程式の解の公式の研究については、紀元前の古代ギリシアのユークリッド(Euclid)やそれ以前にまで遡るが、ゼロの概念が無かったことや、17世紀まで負の数が認められなかったため、負の数を回避する形式で制限的なものであった。7世紀のインドの数学者であるブラフマグプタ(Brahmagupta)は、その著書の中で二次方程式の解の公式を言葉で明示していた。
今日知られている形式での二次方程式の解の公式は、ルネ・デカルト(René Descartes)の1637年の著書『La Géométrie』(幾何学)において見られた。
三次方程式の解
さて、ここでは、前回の研究員の眼でも説明したように、虚数や複素数の概念の導入の契機となった三次方程式の解に関する話題について、述べておく。
古代バビロニアにおいて既に代数的解法4が発見されていたと考えられている二次方程式と違い、三次方程式の代数的解法については、(前回の研究員の眼で簡単に触れたように)シピオーネ・デル・フェッロ(Scipione del Ferro)とニコロ・フォンタナ(通称タルタリア)(Niccolò Fontana "Tartaglia")による解法に基づいて、ジェラロモ・カルダノ(Gerolamo Cardano)が1545年の著書『Ars Magna(アルス・マグナ)』において、三次方程式の解の公式(併せて、ルドヴィコ・フェラーリ(Ludovico Ferrari)による四次方程式の代数的解法)を公表してからだった。
三次方程式は、代数学の基本定理により、高々3つの複素数解を有する。
この3つの複素数解については、以下のことが成り立つ(ここでは、結果のみを示しておく)。
実数を係数とする三次方程式
古代バビロニアにおいて既に代数的解法4が発見されていたと考えられている二次方程式と違い、三次方程式の代数的解法については、(前回の研究員の眼で簡単に触れたように)シピオーネ・デル・フェッロ(Scipione del Ferro)とニコロ・フォンタナ(通称タルタリア)(Niccolò Fontana "Tartaglia")による解法に基づいて、ジェラロモ・カルダノ(Gerolamo Cardano)が1545年の著書『Ars Magna(アルス・マグナ)』において、三次方程式の解の公式(併せて、ルドヴィコ・フェラーリ(Ludovico Ferrari)による四次方程式の代数的解法)を公表してからだった。
三次方程式は、代数学の基本定理により、高々3つの複素数解を有する。
この3つの複素数解については、以下のことが成り立つ(ここでは、結果のみを示しておく)。
実数を係数とする三次方程式
に基づいて、
・Δ2 = 0 の時、三重解を持つ。
・Δ2 ≠ 0 の時、1個の二重解と実数解を1個持ち、以下の通りとなる。
Δ2 > 0 の時(二重解)<(もう一つの実数解)
Δ2 < 0 の時(二重解)>(もう一つの実数解)
なお、三次方程式の3つの解α1、α2、α3については、以下が成り立つ。
α1+α2+α3=-a2/a3、α1α2+α2α3+α3α1= a1/a3、α1α2α3=-a0/a3
4 「代数的解法」とは、係数に対する四則演算と冪根をとる操作の有限回の組合せ、による解法。
・Δ2 = 0 の時、三重解を持つ。
・Δ2 ≠ 0 の時、1個の二重解と実数解を1個持ち、以下の通りとなる。
Δ2 > 0 の時(二重解)<(もう一つの実数解)
Δ2 < 0 の時(二重解)>(もう一つの実数解)
なお、三次方程式の3つの解α1、α2、α3については、以下が成り立つ。
α1+α2+α3=-a2/a3、α1α2+α2α3+α3α1= a1/a3、α1α2α3=-a0/a3
4 「代数的解法」とは、係数に対する四則演算と冪根をとる操作の有限回の組合せ、による解法。
(2025年05月28日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
| 2025/09/12 | 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月14日
今週のレポート・コラムまとめ【10/7-10/10発行分】 -
2025年10月10日
企業物価指数2025年9月~国内企業物価の上昇率は前年比2.7%、先行きは鈍化予想~ -
2025年10月10日
中期経済見通し(2025~2035年度) -
2025年10月10日
保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など -
2025年10月10日
若者消費の現在地(4)推し活が映し出す、複層的な消費の姿~データで読み解く20代の消費行動
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【複素数について(その2)-複素数と方程式-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
複素数について(その2)-複素数と方程式-のレポート Topへ


















 となる。
となる。








 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




