- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 小数について(その1)-小数の起源や記法等はどうなっているのか-
コラム
2023年01月23日
文字サイズ
- 小
- 中
- 大
はじめに
小数という概念は、今からすれば、極めて便利なものとなっているが、分数の考え方が古代エジプトの時代から使用されていたのに比べて、小数点の概念を明示的に含む形で小数が使用されるようになったのは、近代になってからであり、現在のような形に定着したのはそんなに古い話ではない。
小数を巡る話題について、4回に分けて報告することにするが、今回はまずはその起源や記法等について述べることとする。
小数を巡る話題について、4回に分けて報告することにするが、今回はまずはその起源や記法等について述べることとする。
小数とは
「小数(decimal)」は、位取り記数法1と小数点を用いて実数を表現するための表記法である。
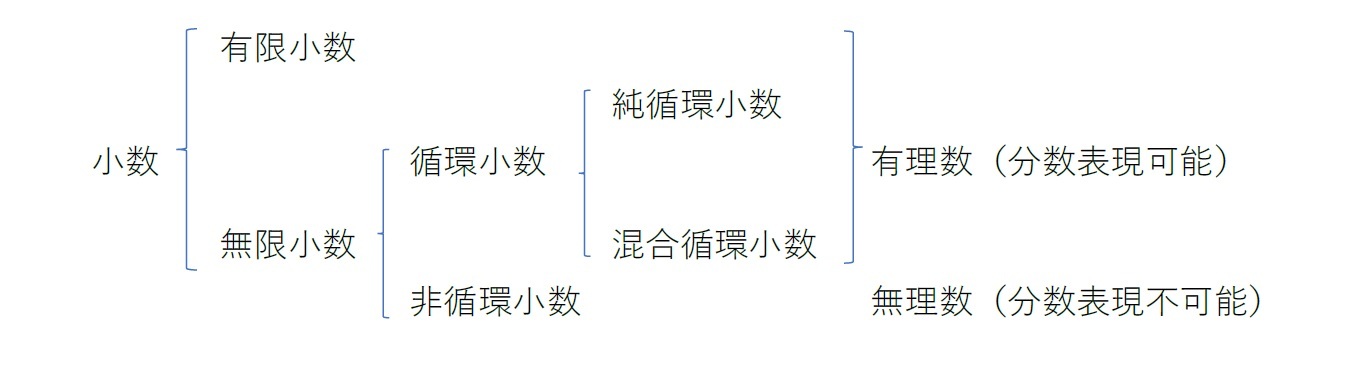
小数には、有限桁の数字で表現される「有限小数」と有限桁の数字では表現できない「無限小数」がある。さらに、無限小数は、同じ数字列が無限に繰り返される「循環小数」とそれ以外の「非循環小数」に区分される。
有限小数と循環小数は、n/m(n、mは互いに素な整数で、m≠0)といった形で分数表現が可能で「有理数」と言われ、非循環小数は、分数表現が不可能で「無理数」と呼ばれる2。
さらに、次回の研究員の眼で詳しく説明するように、循環小数は、繰り返される数字の列(これを「循環節」という)が小数第一位から始まる「純循環小数」と、循環節が小数第二位以降で始まる「混合循環小数(あるいは混循環小数)」に区分される。なお、小数点より左を「整数部(分)」、右を「小数部(分)」と呼んで区分しているが、整数部が0となっている小数(例えば、0.123)を「純小数」、整数部が0でない小数(例えば、4.567)を「帯小数」と呼ぶことがある。
結局、小数は、以下のように分類されることになる3。
小数には、有限桁の数字で表現される「有限小数」と有限桁の数字では表現できない「無限小数」がある。さらに、無限小数は、同じ数字列が無限に繰り返される「循環小数」とそれ以外の「非循環小数」に区分される。
有限小数と循環小数は、n/m(n、mは互いに素な整数で、m≠0)といった形で分数表現が可能で「有理数」と言われ、非循環小数は、分数表現が不可能で「無理数」と呼ばれる2。
さらに、次回の研究員の眼で詳しく説明するように、循環小数は、繰り返される数字の列(これを「循環節」という)が小数第一位から始まる「純循環小数」と、循環節が小数第二位以降で始まる「混合循環小数(あるいは混循環小数)」に区分される。なお、小数点より左を「整数部(分)」、右を「小数部(分)」と呼んで区分しているが、整数部が0となっている小数(例えば、0.123)を「純小数」、整数部が0でない小数(例えば、4.567)を「帯小数」と呼ぶことがある。
結局、小数は、以下のように分類されることになる3。
1 予め定められた一定数の種類の数字(記号)(その個数を「基数」と呼ぶ)を並べて、各数字(記号)が置かれている位置で、それぞれの位(桁)を表す方法。基数がNの場合に 「N進位取り記数法」あるいは単に「N進法」と呼ぶ。
2 以下では、主として十進法をイメージして記載しているが、より一般的なN進法においても、同様な概念が存在している。有理数であるか無理数であるか(即ち、非循環小数となるか否か)は基数によらないが、有理数が有限小数となるか循環小数となるかは、基数即ち何進法で表示するのかに依存する。例えば十進法では1/3は循環小数だが、三進法では0.1となり有限小数となる。
3 なお、有限小数も、有限桁以降に「0」あるいは「9」が循環する等と考えれば、即ち、例えば、1/4=0.25=0.25000…=0.24999… のように表現すれば、循環小数とみなすことができることになる(ただし、「0」は「9」が循環する形では表現できない)。
小数の起源-バビロニア(六十進法による)-
ただし、小数点が存在しないことから、整数部分と小数部分の区別が出来なかった。位取りの取り方によって、例えば、上記の数字は、以下のように複数の形に読めることになる。
12×60+3=723
12+3×1/60=12.05
12×1/60+3 ×(1/60)2=0.2008333……
これについて、実際の数の位は、それが使用されている文脈の前後等の状況に応じて判断していたようである。
4 六十進法が使用されていた理由としては、60という数字が多くの約数(1,2,3,4,5,6,10,12,15,20,30,60)を有しており、古くから指を使って数を数えていたこととの関係から、片手の指の本数である5までの全ての自然数で割り切れることができることが関係していたと考えられている。なお、六十進法とはいっても、1と10を表す楔形文字が基本的な表示として使用されており、いわば十進法が基本にあって、位取りは六十進法で行われていた形になっている。一松 信氏は、その著書「数の世界-概念の形成と認知-」(丸善出版)の中で、これを「十・六進法」と称している。
5 さらには、これらの数を使用して、四則演算も行われていた。
12×60+3=723
12+3×1/60=12.05
12×1/60+3 ×(1/60)2=0.2008333……
これについて、実際の数の位は、それが使用されている文脈の前後等の状況に応じて判断していたようである。
4 六十進法が使用されていた理由としては、60という数字が多くの約数(1,2,3,4,5,6,10,12,15,20,30,60)を有しており、古くから指を使って数を数えていたこととの関係から、片手の指の本数である5までの全ての自然数で割り切れることができることが関係していたと考えられている。なお、六十進法とはいっても、1と10を表す楔形文字が基本的な表示として使用されており、いわば十進法が基本にあって、位取りは六十進法で行われていた形になっている。一松 信氏は、その著書「数の世界-概念の形成と認知-」(丸善出版)の中で、これを「十・六進法」と称している。
5 さらには、これらの数を使用して、四則演算も行われていた。
小数の起源-古代中国(十進法による)-
現代の小数と同じ十進法における小数については、記録に残るところでは、古代中国が最古とされる6。紀元前1世紀から紀元後2世紀に制作されたとされる数学書「九章算術」があるが、魏の劉徽(りゅうき)が紀元後263年に、この数学書の注釈本を著していて、その中で分数と併記の形で小数について記載されている。具体的には「開平術」に関する記述の中で、「微数」という用語で小数を表現し、「小数でもう名称がないものは、其の一退は十を以て母と為す。其の再退は百を以て母と為す」(微細な数が単位を持たなければ分子として、それが位を一つ下げたものならば10を分母とする。それが位をさらに下げたものならば100を分母とする(「九章算術」訳注稿(10) 田村 誠、吉村昌之 による)と記載されている。
中国においては、「漢数字」によって数が表記されるが、これには十進法の数詞が使用されている。例えば、50は「五十」、54は「五十四」、15は「十五」というような形で、1から9までの数字を表す「一、二、三、四、五、六、七、八、九」と10の累乗の数字を表す「十、百、千、万」等を組み合わせて、数字を表している7。
中国では、秦が中国を統一した後、度量衡の単位が統一されていったが、その後の過程を経て、整数部に度量衡の単位を付け、小数部に「分(ぶ)」「釐(り)」「毫(ごう)」「絲(し)」「忽(こつ)」等の単位が付けられたものが使用されて、汎用的な小数が表現されていた。これによれば、例えば、度(長さ)の19.58寸は「一尺九寸五分八釐」、衡(質量)の19.58 錢は「一兩九錢五分八釐」と表現され、0.58 を表す「五分八釐」は共通の表現になっていた。
ただし、これらはあくまでも度量衡の単位で、計算に便利な「無名数」(長さや重さの単位等の助数詞が何も付いていない数)のようなものではなかった。
6 古代中国においても、独自の数学が発展していたと思われるが、紀元前213年に秦の始皇帝が行った焚書政策により、それ以前に書かれた数学の書籍が焼かれてしまったため、秦以前の数学を知ることができない状況にある。
7 漢数字による、この方式から、10の累乗を表す記号を除いて、単純に数字の位置だけで位を表すようにしたものが、現在の「位取り記数法」になる。
中国においては、「漢数字」によって数が表記されるが、これには十進法の数詞が使用されている。例えば、50は「五十」、54は「五十四」、15は「十五」というような形で、1から9までの数字を表す「一、二、三、四、五、六、七、八、九」と10の累乗の数字を表す「十、百、千、万」等を組み合わせて、数字を表している7。
中国では、秦が中国を統一した後、度量衡の単位が統一されていったが、その後の過程を経て、整数部に度量衡の単位を付け、小数部に「分(ぶ)」「釐(り)」「毫(ごう)」「絲(し)」「忽(こつ)」等の単位が付けられたものが使用されて、汎用的な小数が表現されていた。これによれば、例えば、度(長さ)の19.58寸は「一尺九寸五分八釐」、衡(質量)の19.58 錢は「一兩九錢五分八釐」と表現され、0.58 を表す「五分八釐」は共通の表現になっていた。
ただし、これらはあくまでも度量衡の単位で、計算に便利な「無名数」(長さや重さの単位等の助数詞が何も付いていない数)のようなものではなかった。
6 古代中国においても、独自の数学が発展していたと思われるが、紀元前213年に秦の始皇帝が行った焚書政策により、それ以前に書かれた数学の書籍が焼かれてしまったため、秦以前の数学を知ることができない状況にある。
7 漢数字による、この方式から、10の累乗を表す記号を除いて、単純に数字の位置だけで位を表すようにしたものが、現在の「位取り記数法」になる。
(参考)中国における「算木」による数の表現
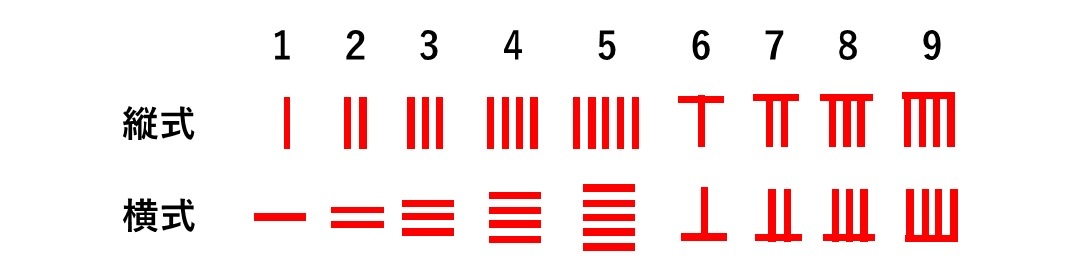
中国では、紀元前2世紀頃から、計算用に「算木(さんぎ)」8が使用されており、これには世界最古とされる位取り記数法が使用されていた。赤の算木で正の数を、黒の算木で負の数を、「0」はその場所に算木を置かず空けておく(「無入(むにゅう)」という。後に、碁石を置いたり、「〇」を書いたりするようになった)ことで表された。また、位取りの違いを明確にするために、算木の向きを変えて、縦式(縦に置く方式)で奇数桁、横式(横に置く方式)で偶数桁を表していた。
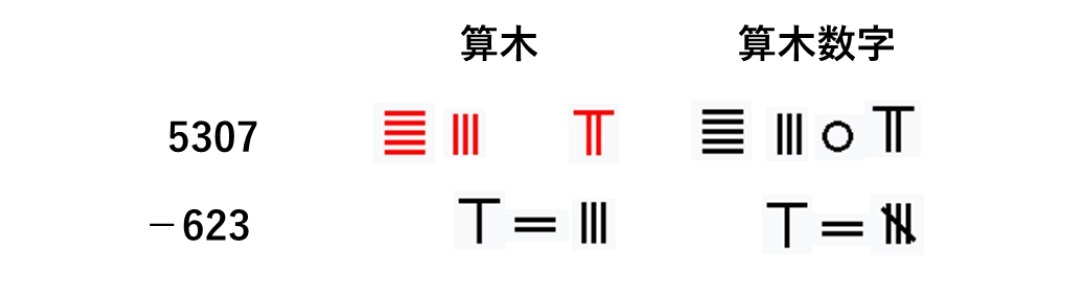
さらには、時代と共に、1の位の右側にも算木を置くことで、小数点以下の位も表すことも行われていくようになっていった。
具体的には、正の数は、以下の通りとなっている(負の数は、同じものが黒くなっている)9。
さらには、時代と共に、1の位の右側にも算木を置くことで、小数点以下の位も表すことも行われていくようになっていった。
具体的には、正の数は、以下の通りとなっている(負の数は、同じものが黒くなっている)9。
8 算木は、長さ 3 ~ 14cm の木製又は竹製の細長い直方体で、縦又は横に並べて数を表し、配列を動かすことで四則演算等の計算を行う。現代のそろばんの開発に影響を与えたとされている。
9 この図からわかるように5を表す数字を2個合わせて10とする形になっており、一松 信氏も先に述べた著書の中で、このような場合「五・二進法」と呼ぶのが適切、ではないかと述べている。
小数の起源-イスラム圏(十進法による)-
イスラム圏においても、十進法による小数表記が、インドを経由して10世紀から広がっていった。
アラブの数学者のアル=ウクリーディスィーは、952年頃の著書「インドの算術」の中で、0の上の縦の印で十進小数部分がその桁から始まることを示していた。また、ペルシャの天文学者かつ数学者のアル・カーシー(1380-1429)は、1427年の著書「計算法の鍵」の中で、十進小数についての解説を行っているが、そこでは整数部分と小数部分の区別に縦棒を使う以外に、色によって分ける等の工夫も凝らしていた(「非ヨーロッパ起源の数学」(G.G.ジョゼフ著、垣田高夫、大町比佐栄 訳 講談社)に基づく)。
このように、イスラム圏での小数の使用は、西洋に比べて進んでいた。
アラブの数学者のアル=ウクリーディスィーは、952年頃の著書「インドの算術」の中で、0の上の縦の印で十進小数部分がその桁から始まることを示していた。また、ペルシャの天文学者かつ数学者のアル・カーシー(1380-1429)は、1427年の著書「計算法の鍵」の中で、十進小数についての解説を行っているが、そこでは整数部分と小数部分の区別に縦棒を使う以外に、色によって分ける等の工夫も凝らしていた(「非ヨーロッパ起源の数学」(G.G.ジョゼフ著、垣田高夫、大町比佐栄 訳 講談社)に基づく)。
このように、イスラム圏での小数の使用は、西洋に比べて進んでいた。
小数の起源-欧州(十進法による)-
これに対して、欧州においては、エジプト式の分数表記10が普及していたため、小数の導入は遅れた。欧州で初めて小数を提唱したのは、ベルギーのブルージュ出身のオランダ軍主計将校だったシモン・ステヴィン(Simon Stevin)(1548-1620)だった11。1585年に出版した「十進分数論」(あるいは「十分の一法」)(「De Thiende(フランドル語版)」、及びその後の同じ年の「La disme(フランス語版)」)の中で、十進法による小数の理論を提唱した。それまでの分数を用いた計算では、非常に複雑になるケースもあった中で、ステヴィンの提唱した小数の表記法は、例えば、「4.732」であれば、これを「4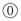 07①3②2③」(即ち、小数点に相当する部分に
07①3②2③」(即ち、小数点に相当する部分に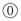 、小数第一位の数字に①、小数第二位の数字に②、小数第三位の数字に③を付与して)表記した。ステヴィンは、これにより、四則演算を、分数を用いることなく、整数によって行うことができる、と記している。
、小数第一位の数字に①、小数第二位の数字に②、小数第三位の数字に③を付与して)表記した。ステヴィンは、これにより、四則演算を、分数を用いることなく、整数によって行うことができる、と記している。
その約20年後に、対数の発見者として知られ、ネイピア数eで有名な英国の数学者ジョン・ネイピア(John Napier)(1550-1617)が、整数と小数の間に記号を入れることで、①や②等の表記を行わない、現代のような小数点による表記を提唱した。ネイピアは、小数点として、最初は「点(.)」(又は「ピリオド」)ないしは「コンマ(,)」を使用していたが、死後の1619年に出版された対数表の作成に関する著書「対数の素晴らしい規則の構成(Mirifici logarithmorum canonis constructio)」では、ピリオドだけを使用していた12。これが対数表に使用されるようになって、対数の普及とともに、徐々に世界中に広まっていくことになった。これにより、小数を扱う計算が便利になっていった。
このように、欧州において、現在のような小数点を使った十進法による小数の表記が実現するのは、16世紀後半から17世紀初めになってからであり、さらに社会に定着していくのは17世紀末になってから、ということになっている。
10 エジプトの数学やその分数表記については、次回の「分数について」の研究員の眼のシリーズの中で報告する。
11 なお、「小数と対数の発見」山本義隆 日本評論社(2018)によれば、西欧においてステヴィン以前にも小数を使用した例は散見されるが、それらは「断片的であり、かつ部分的でしかなかった」とされ、「単に小数の記数法を考案しただけでなく、10進小数の意義を十分に理解し、そのアルゴリズムを正確に論じることによって、10進小数を数学理論の内部にはじめて明確に位置付けた」のが、ステヴィンだったとされている。なお、ステヴィンは、これを通じて、それまで整数の比で表されないことで受け容れられてなかった無理数も、他の数と同様に受け容れている。
12 なお、小数点の記号を広めたのは、ネイピアと同時代にネイピアとは独立に対数を発見したスイスの時計職人ヨスト・ビュルギ(Jost Bürgi)(1558-1632)であると言われている。
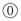 07①3②2③」(即ち、小数点に相当する部分に
07①3②2③」(即ち、小数点に相当する部分に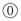 、小数第一位の数字に①、小数第二位の数字に②、小数第三位の数字に③を付与して)表記した。ステヴィンは、これにより、四則演算を、分数を用いることなく、整数によって行うことができる、と記している。
、小数第一位の数字に①、小数第二位の数字に②、小数第三位の数字に③を付与して)表記した。ステヴィンは、これにより、四則演算を、分数を用いることなく、整数によって行うことができる、と記している。その約20年後に、対数の発見者として知られ、ネイピア数eで有名な英国の数学者ジョン・ネイピア(John Napier)(1550-1617)が、整数と小数の間に記号を入れることで、①や②等の表記を行わない、現代のような小数点による表記を提唱した。ネイピアは、小数点として、最初は「点(.)」(又は「ピリオド」)ないしは「コンマ(,)」を使用していたが、死後の1619年に出版された対数表の作成に関する著書「対数の素晴らしい規則の構成(Mirifici logarithmorum canonis constructio)」では、ピリオドだけを使用していた12。これが対数表に使用されるようになって、対数の普及とともに、徐々に世界中に広まっていくことになった。これにより、小数を扱う計算が便利になっていった。
このように、欧州において、現在のような小数点を使った十進法による小数の表記が実現するのは、16世紀後半から17世紀初めになってからであり、さらに社会に定着していくのは17世紀末になってから、ということになっている。
10 エジプトの数学やその分数表記については、次回の「分数について」の研究員の眼のシリーズの中で報告する。
11 なお、「小数と対数の発見」山本義隆 日本評論社(2018)によれば、西欧においてステヴィン以前にも小数を使用した例は散見されるが、それらは「断片的であり、かつ部分的でしかなかった」とされ、「単に小数の記数法を考案しただけでなく、10進小数の意義を十分に理解し、そのアルゴリズムを正確に論じることによって、10進小数を数学理論の内部にはじめて明確に位置付けた」のが、ステヴィンだったとされている。なお、ステヴィンは、これを通じて、それまで整数の比で表されないことで受け容れられてなかった無理数も、他の数と同様に受け容れている。
12 なお、小数点の記号を広めたのは、ネイピアと同時代にネイピアとは独立に対数を発見したスイスの時計職人ヨスト・ビュルギ(Jost Bürgi)(1558-1632)であると言われている。
小数の起源-日本-
日本には、江戸時代の初めに中国から小数の考え方が伝わったと言われている。「小数」については、江戸時代の数学者(和算家)である吉田光由(1598~1673)が寛永年間(1630年頃)に著した「塵劫記(じんこうき)」に、『小かずの名の事』等として、分、厘、毛、糸等の1より小さくなっていく位としての各種の位の名称が紹介されている。
日本における漢数字の数詞に関しては、基本的には中国語に基づいているが、いくつかの単位は使う字が変更され、釐は厘(りん)に、毫は毛(もう)に、絲は糸になっている。
日本における漢数字の数詞に関しては、基本的には中国語に基づいているが、いくつかの単位は使う字が変更され、釐は厘(りん)に、毫は毛(もう)に、絲は糸になっている。
(2023年01月23日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月28日
試練の5年に踏み出す中国(前編)-「第15次五カ年計画」の5年間は、どのような5年か -
2025年10月28日
地域医療連携推進法人の現状と今後を考える-「連携以上、統合未満」で協力する形態、その将来像は? -
2025年10月28日
東宝の自己株式取得-公開買付による取得 -
2025年10月28日
今週のレポート・コラムまとめ【10/21-10/27発行分】 -
2025年10月27日
大学卒女性の働き方別生涯賃金の推計(令和6年調査より)-正社員で2人出産・育休・時短で2億円超
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【小数について(その1)-小数の起源や記法等はどうなっているのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
小数について(その1)-小数の起源や記法等はどうなっているのか-のレポート Topへ




















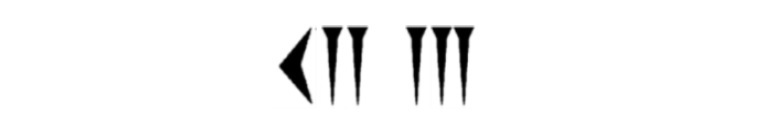

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




