- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無理数について(その1)-無理数同士や有理数との四則演算結果はどうなっているのだろう(πとeの和・積は無理数なのか)-
コラム
2021年12月01日
文字サイズ
- 小
- 中
- 大
はじめに
以前の数学記号の由来シリーズの第8回で「数を表す記号」について報告したが、その中で「無理数」についても説明した。その中で、無理数については、これを表す一文字の記号等はなく、その理由として、「無理数が単独で扱われる機会が少なく、あくまでも実数の中での有理数でない数として扱われることが多いことによるものと思われる。」と述べた。
ところが、無理数の中のいくつかのものは、e(ネイピア数)やπ(円周率)に代表されるように、数学記号で表されて、日常生活の中でも接触する機会が多くあって、ある意味でなじみ深いものとなっている。
今後の複数回の研究員の眼では、この無理数に関する話題について紹介したい。
まずは今回の研究員の眼では、無理数の定義や区分と無理数同士や有理数との四則演算結果等について紹介する。
ところが、無理数の中のいくつかのものは、e(ネイピア数)やπ(円周率)に代表されるように、数学記号で表されて、日常生活の中でも接触する機会が多くあって、ある意味でなじみ深いものとなっている。
今後の複数回の研究員の眼では、この無理数に関する話題について紹介したい。
まずは今回の研究員の眼では、無理数の定義や区分と無理数同士や有理数との四則演算結果等について紹介する。
無理数とは
「無理数」は、英語では「irrational number」と呼ばれる。これは「有理数」が「rational number」と呼ばれることに対して、有理数以外の実数であることから、こうした名称となっている。「有理数」は「2つの整数a、b(≠ 0)を用いて、a/b という分数で表せる実数」のことを指しており、「無理数は」、「2つの整数a、b(≠ 0)を用いて、a/b という分数で表せない実数」を指していることになる。
実は、こうした定義から、有理数は、分数の比で表せる数であり、「ratio」が「比」を意味することから、「有比数」と訳し、無理数のことを「無比数」と呼ぶべきではないかとの意見もある。
なお、有理数を小数表示した場合には、「有限小数」又は「循環小数」となるが、無理数を小数表示すると、循環しない無限小数となる。これは、もしある数αが小数点のn桁からm個連続する循環小数であったとすると、10n-1+m×α-10n-1×α は、循環部分が相殺されて、整数βになるため、
α=β/(10n-1+m-10n-1)となり、αは有理数となるからである。
なお、有理数は可算個1であるのに対して、無理数は非可算個であり、殆どの実数は無理数、ということになっている。
1 「可算(countable)」というのは、無限集合の全ての元と自然数の集合{1,2,3,…}との間に一対一対応がつけられることをいう。
実は、こうした定義から、有理数は、分数の比で表せる数であり、「ratio」が「比」を意味することから、「有比数」と訳し、無理数のことを「無比数」と呼ぶべきではないかとの意見もある。
なお、有理数を小数表示した場合には、「有限小数」又は「循環小数」となるが、無理数を小数表示すると、循環しない無限小数となる。これは、もしある数αが小数点のn桁からm個連続する循環小数であったとすると、10n-1+m×α-10n-1×α は、循環部分が相殺されて、整数βになるため、
α=β/(10n-1+m-10n-1)となり、αは有理数となるからである。
なお、有理数は可算個1であるのに対して、無理数は非可算個であり、殆どの実数は無理数、ということになっている。
1 「可算(countable)」というのは、無限集合の全ての元と自然数の集合{1,2,3,…}との間に一対一対応がつけられることをいう。
無理数の例とその証明例
学生時代に学んだように、有名な無理数としては、例えば以下のような数が挙げられる。
√2、√3、√5、√6、√7 等(より一般的に「平方数でない数の平方根」等も無理数)
log2、log3 等
円周率 π
ネイピア数 e
このうち、例えば、「√2が無理数であることの証明」は、いくつかの証明法があるが、以下では定番の背理法を用いて証明しておく。同様の背理法で、√3、√5 等が無理数であることが証明される。
(証明)√2が有理数であるとすると、互いに素な自然数pとqを用いて、√2=q/p と表されることから、両辺を二乗して分母を払うと、2p2=q2、左辺は2の倍数になるのでq2は2の倍数、よってqも2の倍数
そこで、q=2r とおくと、2p2=q2=4r2、よって p2=2r2となり、pも2の倍数いうことになる。
これはpとqが互いに素であるという前提に矛盾
また、「ネイピア数eが無理数であることの証明」は、1744年にレオンハルト・オイラー(Leonhard Euler)が初めて行っている。ここでは、ジョセフ・フーリエ(Joseph Fourier)による証明として、eを底とする指数関数exのマクローリン展開に基づいて、eを以下のように定義することで、背理法により証明する。
√2、√3、√5、√6、√7 等(より一般的に「平方数でない数の平方根」等も無理数)
log2、log3 等
円周率 π
ネイピア数 e
このうち、例えば、「√2が無理数であることの証明」は、いくつかの証明法があるが、以下では定番の背理法を用いて証明しておく。同様の背理法で、√3、√5 等が無理数であることが証明される。
(証明)√2が有理数であるとすると、互いに素な自然数pとqを用いて、√2=q/p と表されることから、両辺を二乗して分母を払うと、2p2=q2、左辺は2の倍数になるのでq2は2の倍数、よってqも2の倍数
そこで、q=2r とおくと、2p2=q2=4r2、よって p2=2r2となり、pも2の倍数いうことになる。
これはpとqが互いに素であるという前提に矛盾
また、「ネイピア数eが無理数であることの証明」は、1744年にレオンハルト・オイラー(Leonhard Euler)が初めて行っている。ここでは、ジョセフ・フーリエ(Joseph Fourier)による証明として、eを底とする指数関数exのマクローリン展開に基づいて、eを以下のように定義することで、背理法により証明する。
(証明)eが有理数であるとすると、互いに素な自然数pとqを用いて、e=q/p と表されることから、両辺にp!をかけることで、Nを自然酢として、以下の通りとなる。
(p-1)!=N+1 /(p+1)+1/(p+1)(p+2)+1/(p+1)(p+2)(p+3) +……
これにより、
(p-1)!-N=1 /(p+1)+1/(p+1)(p+2)+1/(p+1)(p+2)(p+3) +……
<1/2+1/22+1/23+…… =1
これは左辺が自然数であることと矛盾する。
一方で、「πが無理数であることの証明」は難しい。πが無理数であることは紀元前4世紀のアリストテレスが予想していたようだが、実際に証明されたのは18世紀になってからである。
(p-1)!=N+1 /(p+1)+1/(p+1)(p+2)+1/(p+1)(p+2)(p+3) +……
これにより、
(p-1)!-N=1 /(p+1)+1/(p+1)(p+2)+1/(p+1)(p+2)(p+3) +……
<1/2+1/22+1/23+…… =1
これは左辺が自然数であることと矛盾する。
一方で、「πが無理数であることの証明」は難しい。πが無理数であることは紀元前4世紀のアリストテレスが予想していたようだが、実際に証明されたのは18世紀になってからである。
超越数と代数的数
なお、πやeは、以前の研究員の眼で述べたように、「超越数」と呼ばれるものに区分される。
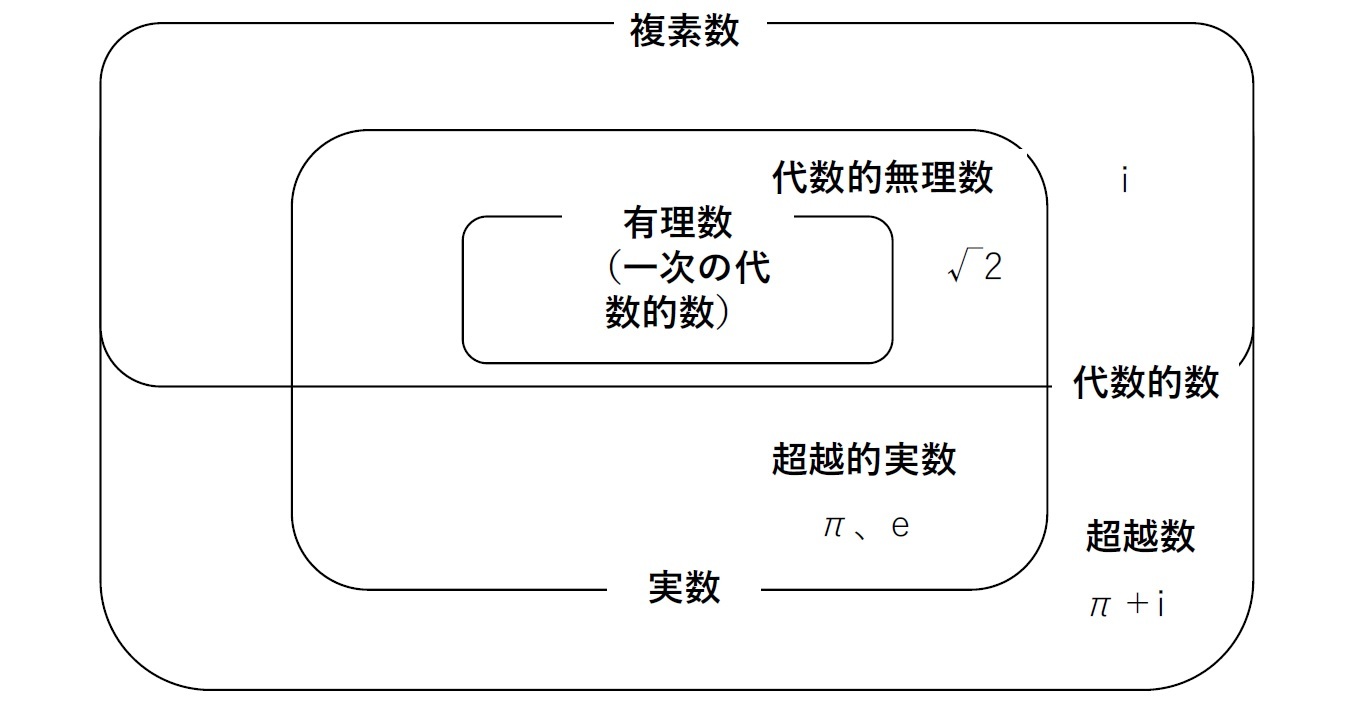
「超越数(transcendental number)」というのは、有理数を係数にもついかなる代数方程式の解とはなりえない数(すなわち、どんな有理数 a0,a1,…,an を係数とする n 次の代数方程式 a0xn+a1xn-1+…+an-1x+an=0 の解にもならないような数)のことである。複素数(実数を含む)の中で,超越数でないものは「代数的数(algebraic number)」と呼ばれる。
有理数は一次方程式の解であるから、超越的な実数はすべて無理数になるが、無理数 √2 は x2 − 2 = 0 の解であるから、逆は成り立たない。則ち、無理数は超越数と「代数的無理数」と呼ばれる超越数でない無理数に区分される。
複素数(実数を含む)の中で,超越数でないもの(代数的数)は可算個しかなく,この意味で,複素数の大部分は超越数となる。
なお、「eが超越数であることの証明」は、1873年にフランスの数学者のシャルル・エルミート(Charles Hermite)が、「πが超越数であることの証明」は、1882年にドイツの数学者のフェルディナント・フォン・リンデマン(Ferdinand von Lindemann)が行っている。
一般的に、ある数が超越数であることの証明は、無理数であることの証明よりもかなり難しくなる。
「超越数(transcendental number)」というのは、有理数を係数にもついかなる代数方程式の解とはなりえない数(すなわち、どんな有理数 a0,a1,…,an を係数とする n 次の代数方程式 a0xn+a1xn-1+…+an-1x+an=0 の解にもならないような数)のことである。複素数(実数を含む)の中で,超越数でないものは「代数的数(algebraic number)」と呼ばれる。
有理数は一次方程式の解であるから、超越的な実数はすべて無理数になるが、無理数 √2 は x2 − 2 = 0 の解であるから、逆は成り立たない。則ち、無理数は超越数と「代数的無理数」と呼ばれる超越数でない無理数に区分される。
複素数(実数を含む)の中で,超越数でないもの(代数的数)は可算個しかなく,この意味で,複素数の大部分は超越数となる。
なお、「eが超越数であることの証明」は、1873年にフランスの数学者のシャルル・エルミート(Charles Hermite)が、「πが超越数であることの証明」は、1882年にドイツの数学者のフェルディナント・フォン・リンデマン(Ferdinand von Lindemann)が行っている。
一般的に、ある数が超越数であることの証明は、無理数であることの証明よりもかなり難しくなる。
無理数の四則演算
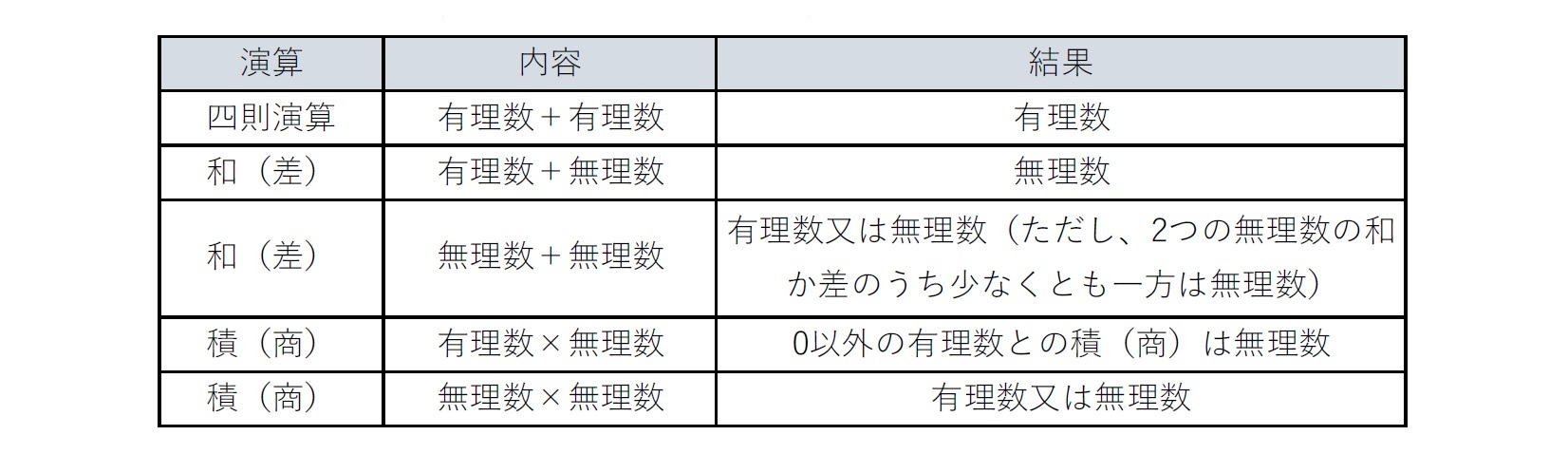
有理数は四則演算(和、差、積、商)に関して閉じている。即ち、有理数の四則演算の結果は必ず有理数になる。これに対して、無理数は四則演算(和、差、積、商)に関して閉じていない。即ち、無理数の四則演算の結果は、有理数にも無理数にもなる。さらに先に述べた区分で言えば、代数的数は四則演算に関して閉じているが、超越数は四則演算に関して閉じていない。
以下で、無理数に関しての具体的な例を示していく。
以下で、無理数に関しての具体的な例を示していく。
無理数と無理数の四則演算
まずは、「無理数の和や積が有理数にも無理数にもなる」例は、以下の通りである。
(1) 無理数+無理数=有理数の例 √2+(―√2)=0
(2) 無理数+無理数=無理数の例 √2+√2)=2√2
(3) 無理数×無理数=有理数の例 √2×√2=2
(4) 無理数×無理数=無理数の例 √2×√3=√6
これを見て、(1)と(3)の例として、同じ平方根による無理数の結果を並べているので、もっと別の例はないのかと思われるかもしれない。その意味では、絶対値が等しくない例として、以下の例が挙げられる。
(2+√2)+(2-√2)=4
(2+√2)×(2-√2)=2
より一般的に a 有理数 b 無理数 の場合
(a+b)+(a-b)=2a 有理数 あるいは (a-b)+b =a 有理数
(a+b)-(a-b)=2b 無理数 あるいは a+(b-a)=b 無理数
(a+b)×(a-b)=a2-b2 (bが有理数の平方根ならば、これは有理数)
となる。
これでも、今一つしっくりこない方もおられると思われる。「同種の無理数の符号を変えただけで無い場合や同種の無理数を掛け合わせた場合以外のような、あまり自明とはいえないケースで、全く異なる2つの無理数の和や積が有理数になる例がないのだろうか」と思われるだろう。
これについてはなかなか難しい。
例えば、πとeを用いた、π+eやπ・e については、殆どの人がこれらは無理数だろうと考えると思われるが、実はこれらが無理数であることは証明されていない。その意味では、これらが有理数である可能性も全くゼロではないということになる。
なお、π+eとπ・eのいずれかは無理数であることは簡単に証明される。これは、πとeが根となる2次方程式 x2+(π+e)x+π・e=0 を考えた場合に、π+eとπ・eがともに有理数であるとすると、πとeが代数的数になってしまうが、これは先に述べたようにπとeが超越数であることに矛盾する、からである。
ただし、以下のことは簡単に証明できる。
「2つの無理数の和と差のうち少なくとも一方は無理数」
2つの無理数a、bに対して、(a+b)と(a-b)がともに有理数だとすると、両者の和である2aが有理数となってしまい、これはaが無理数であることに矛盾する。
従って、例えば、π+eとπ-eが無理数であるかどうかはわかっていないが、いずれかは無理数であることになる。
加えて、ここでは証明を示さないが、以下のことも比較的容易に証明される。
「2つの無理数の和(あるいは差)が0でない場合、和と積と商のうち少なくとも1つは無理数」
なお、「2つの無理数の和(あるいは差)が0の場合」は、先に示した√2と-√2のケースのように、和と積と商が全て有理数となることもある。
(1) 無理数+無理数=有理数の例 √2+(―√2)=0
(2) 無理数+無理数=無理数の例 √2+√2)=2√2
(3) 無理数×無理数=有理数の例 √2×√2=2
(4) 無理数×無理数=無理数の例 √2×√3=√6
これを見て、(1)と(3)の例として、同じ平方根による無理数の結果を並べているので、もっと別の例はないのかと思われるかもしれない。その意味では、絶対値が等しくない例として、以下の例が挙げられる。
(2+√2)+(2-√2)=4
(2+√2)×(2-√2)=2
より一般的に a 有理数 b 無理数 の場合
(a+b)+(a-b)=2a 有理数 あるいは (a-b)+b =a 有理数
(a+b)-(a-b)=2b 無理数 あるいは a+(b-a)=b 無理数
(a+b)×(a-b)=a2-b2 (bが有理数の平方根ならば、これは有理数)
となる。
これでも、今一つしっくりこない方もおられると思われる。「同種の無理数の符号を変えただけで無い場合や同種の無理数を掛け合わせた場合以外のような、あまり自明とはいえないケースで、全く異なる2つの無理数の和や積が有理数になる例がないのだろうか」と思われるだろう。
これについてはなかなか難しい。
例えば、πとeを用いた、π+eやπ・e については、殆どの人がこれらは無理数だろうと考えると思われるが、実はこれらが無理数であることは証明されていない。その意味では、これらが有理数である可能性も全くゼロではないということになる。
なお、π+eとπ・eのいずれかは無理数であることは簡単に証明される。これは、πとeが根となる2次方程式 x2+(π+e)x+π・e=0 を考えた場合に、π+eとπ・eがともに有理数であるとすると、πとeが代数的数になってしまうが、これは先に述べたようにπとeが超越数であることに矛盾する、からである。
ただし、以下のことは簡単に証明できる。
「2つの無理数の和と差のうち少なくとも一方は無理数」
2つの無理数a、bに対して、(a+b)と(a-b)がともに有理数だとすると、両者の和である2aが有理数となってしまい、これはaが無理数であることに矛盾する。
従って、例えば、π+eとπ-eが無理数であるかどうかはわかっていないが、いずれかは無理数であることになる。
加えて、ここでは証明を示さないが、以下のことも比較的容易に証明される。
「2つの無理数の和(あるいは差)が0でない場合、和と積と商のうち少なくとも1つは無理数」
なお、「2つの無理数の和(あるいは差)が0の場合」は、先に示した√2と-√2のケースのように、和と積と商が全て有理数となることもある。
有理数と無理数の四則演算
次に、有理数と無理数の四則演算を考えてみると、以下の通りとなる。
まずは、明らかに、「有理数と無理数の和と差は無理数」になる。これが有理数になってしまったら、この有理数に和や差に使用した有理数を加えたり差し引いたりしたものが有理数になってしまい、矛盾するからである。
一方で、以下の例が示すように、有理数と無理数の積は無理数になるとは限らない。
有理数×無理数=有理数の例 0×√2=0
ただし、これも明らかだが、「0以外の有理数と無理数の積や商は無理数」になる。これが有理数になってしまったら、この有理数に積や商に使用した有理数を掛けたりその有理数で割ったりしたものが有理数になってしまい、矛盾するからである。
また、この特別なケースとして、「無理数の逆数は無理数」ということになる。
まずは、明らかに、「有理数と無理数の和と差は無理数」になる。これが有理数になってしまったら、この有理数に和や差に使用した有理数を加えたり差し引いたりしたものが有理数になってしまい、矛盾するからである。
一方で、以下の例が示すように、有理数と無理数の積は無理数になるとは限らない。
有理数×無理数=有理数の例 0×√2=0
ただし、これも明らかだが、「0以外の有理数と無理数の積や商は無理数」になる。これが有理数になってしまったら、この有理数に積や商に使用した有理数を掛けたりその有理数で割ったりしたものが有理数になってしまい、矛盾するからである。
また、この特別なケースとして、「無理数の逆数は無理数」ということになる。
(参考)√n 、π、eの覚え方
代表的な無理数について、学生時代に覚えた語呂合わせを掲載しておく。これよりもさらに詳しい覚え方もあるが、この程度で十分なのではないかと思われる。
√2≒1.41421356 (一夜一夜に人見頃)
√3≒1.7320508 (人並みにおごれや)
√5≒2.2360679. (富士山麓オウム鳴く)
√6≒2.44949 (似よよくよく)
√7≒2.64575 (菜に虫いない)
√8≒2.8287271 (にやにや世に無い)(実は、√8=2√2 なので、これは覚える必要はない)
√10≒3.16227 (み色に鮒)
π≒3.141592653589793238462643383279
(産医師異国に向こう産後厄なく産婦みやしろに虫さんざん闇に鳴く) あるいは
(身一つ世一つ生くに無意味いわくなく身ふみや読む似ろよさんざん闇に泣く」
e ≒2.718281828459o45 (鮒一鉢二鉢一鉢二鉢、しごく惜しい)
なお、英語にも同様な語呂合わせがあるのだろうかと思われる方もおられるかもしれない。英語では、日本語のように1つ1つの数字に何らかのアルファベットを割り当てるということはせずに、各単語の文字数で数字を表している。
例えば、πについては、以下のような文章による語呂合わせがある。
Can I find a trick recalling pi easily(πを簡単に思い出せるトリックはありますか)
これは、文字数で、3.1415926 を表していることになる。
これよりももっと長い語呂合わせもいくつかあるようだ。興味のある方は、専門書等を参照していただきたい。
√2≒1.41421356 (一夜一夜に人見頃)
√3≒1.7320508 (人並みにおごれや)
√5≒2.2360679. (富士山麓オウム鳴く)
√6≒2.44949 (似よよくよく)
√7≒2.64575 (菜に虫いない)
√8≒2.8287271 (にやにや世に無い)(実は、√8=2√2 なので、これは覚える必要はない)
√10≒3.16227 (み色に鮒)
π≒3.141592653589793238462643383279
(産医師異国に向こう産後厄なく産婦みやしろに虫さんざん闇に鳴く) あるいは
(身一つ世一つ生くに無意味いわくなく身ふみや読む似ろよさんざん闇に泣く」
e ≒2.718281828459o45 (鮒一鉢二鉢一鉢二鉢、しごく惜しい)
なお、英語にも同様な語呂合わせがあるのだろうかと思われる方もおられるかもしれない。英語では、日本語のように1つ1つの数字に何らかのアルファベットを割り当てるということはせずに、各単語の文字数で数字を表している。
例えば、πについては、以下のような文章による語呂合わせがある。
Can I find a trick recalling pi easily(πを簡単に思い出せるトリックはありますか)
これは、文字数で、3.1415926 を表していることになる。
これよりももっと長い語呂合わせもいくつかあるようだ。興味のある方は、専門書等を参照していただきたい。
最後に
今回は、無理数の定義や区分と無理数同士や有理数との四則演算結果等について紹介した。
πとeというような無理数同士の和や積が無理数になるのかどうかというような(ほぼ自明だと思われるようなケース等を除けば)直感的にはそれはそうだろうと一般の人が思うような問題でも、その真偽は確認されていなくて、未だ解決できていない問題となっている。
これを聞いて、何となく、数字の奥深さを再認識させられたような気がしないだろうか。
次回の研究員の眼では、「無理数の(無理数や有理数)べき乗」や「無理数度」等について紹介する。
πとeというような無理数同士の和や積が無理数になるのかどうかというような(ほぼ自明だと思われるようなケース等を除けば)直感的にはそれはそうだろうと一般の人が思うような問題でも、その真偽は確認されていなくて、未だ解決できていない問題となっている。
これを聞いて、何となく、数字の奥深さを再認識させられたような気がしないだろうか。
次回の研究員の眼では、「無理数の(無理数や有理数)べき乗」や「無理数度」等について紹介する。
(2021年12月01日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無理数について(その1)-無理数同士や有理数との四則演算結果はどうなっているのだろう(πとeの和・積は無理数なのか)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無理数について(その1)-無理数同士や有理数との四則演算結果はどうなっているのだろう(πとeの和・積は無理数なのか)-のレポート Topへ


















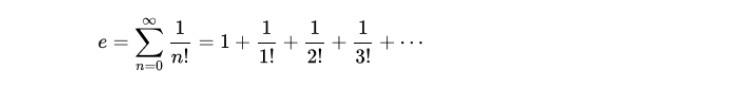

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




