- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 円周率πが現われる世界-ビュフォンの針の問題-
コラム
2017年10月30日
文字サイズ
- 小
- 中
- 大
はじめに
円周率のπ(パイ)については、直径1の円の円周の長さを表す数値として、学生時代に学んでおり、一般の人にも馴染みのある定数である。これまでの研究員の眼の中でも、何度かπについて触れてきた。多くの人が、πは無理数とよばれるもので、その具体的な数値については小数点以下が無限に続くものであるが、ほぼ3.14であると認識しているものと思われる。
それでも、πに対しては、何となく難しい数値で、とっつきにくいものだと思っている人も多いかもしれない。ただし、πという数字は、数学の世界の幅広い場面で現われてくる。今後、πに絡む話題をいくつか紹介していきたいと思う。
今回は、有名な「ビュフォンの針の問題」についてである。
それでも、πに対しては、何となく難しい数値で、とっつきにくいものだと思っている人も多いかもしれない。ただし、πという数字は、数学の世界の幅広い場面で現われてくる。今後、πに絡む話題をいくつか紹介していきたいと思う。
今回は、有名な「ビュフォンの針の問題」についてである。
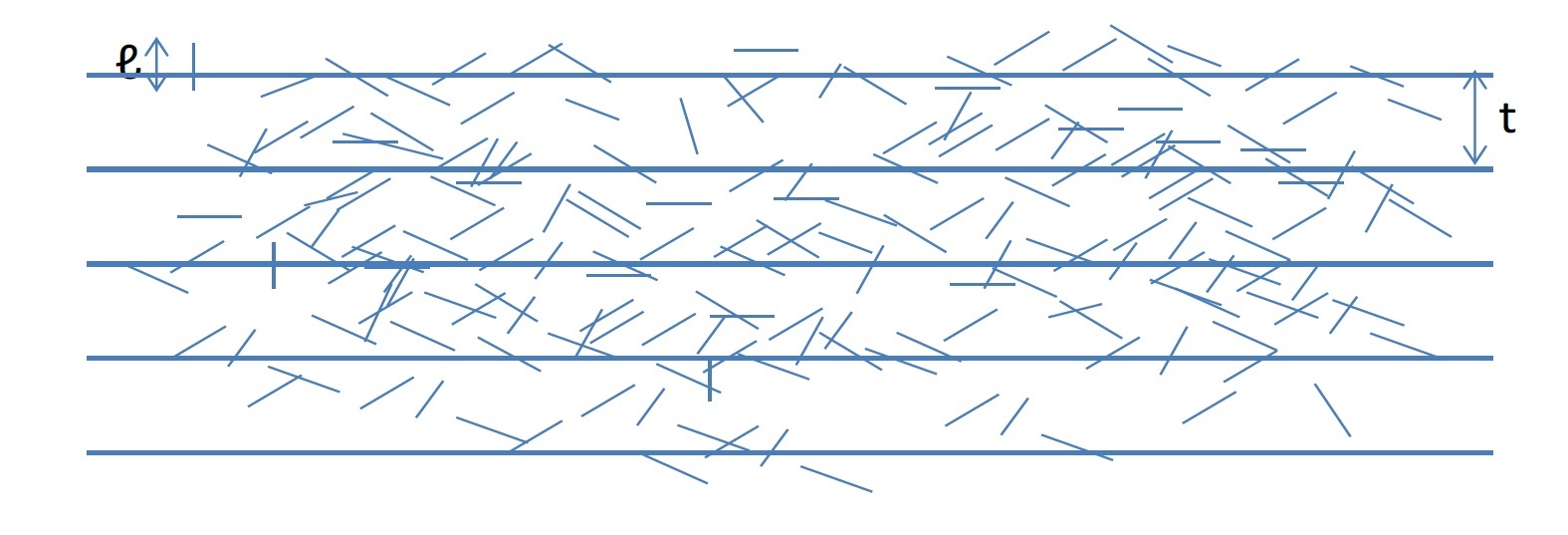
ビュフォンの針の問題
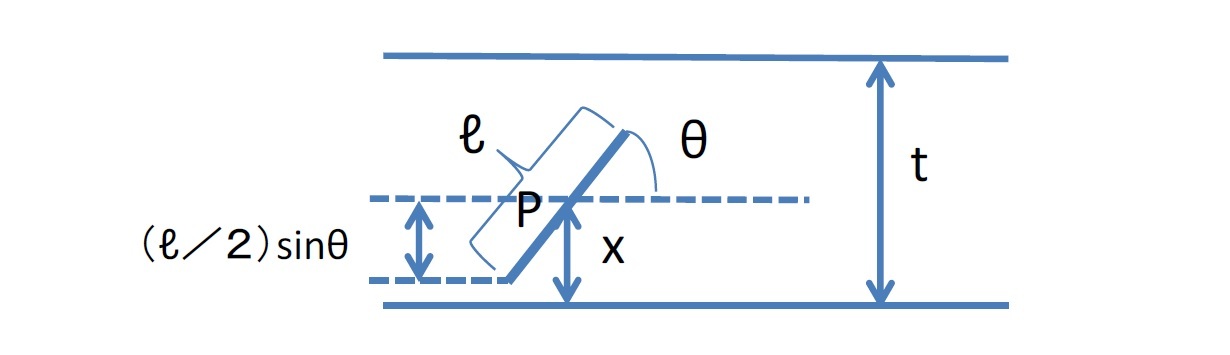
ビュフォンの針の問題の証明
この証明をみていただければわかるように、πが現われてくるのは、針がいろいろな場所に無作為に落ちる状態を表すのに、針の中心点と平行線との距離xに加えて、針と平行線が交わる角度θが用いられ、このθの一様分布を前提に確率を求めていくことになるからである。
言われてしまえば、何だそうかと思われるかもしれないし、それでも今一つしっくりこない方もおられるかもしれない。
言われてしまえば、何だそうかと思われるかもしれないし、それでも今一つしっくりこない方もおられるかもしれない。
補足
針の長さと平行線の間隔の関係という、ちょっとした前提がかわるだけで、結論は極めて複雑なものになってくる。こうしたことは世の中に往々にしてみられるものである。
ビュフォンについて
ビュフォンの針の問題を提案したビュフォン伯爵(Georges-Louis Leclerc, Comte de Buffon)(1707~1788)は、フランスの博物学者、数学者、植物学者である。数学者としてよりも、むしろ博物学者として有名である。ビュフォン伯爵は、天変地異説を否定し、自然は動植物の種を含めて徐々に変化を遂げると考えて、後の進化論の形成に影響を与えている。
さらに、数学の分野では、確率論に微分・積分の概念を導入した。なお、ビュフォンの針の問題は、逆に多くのシミュレーションを行うことで、πの近似値を求めることができることになるため、モンテカルロ法1のルーツとなったとして知られている。
1 モンテカルロ法 (Monte Carlo method) とは、シミュレーションや数値計算を乱数を発生させて行う手法。カジノで有名なモナコ公国の4つある地区の1つの名前に基づいている。
さらに、数学の分野では、確率論に微分・積分の概念を導入した。なお、ビュフォンの針の問題は、逆に多くのシミュレーションを行うことで、πの近似値を求めることができることになるため、モンテカルロ法1のルーツとなったとして知られている。
1 モンテカルロ法 (Monte Carlo method) とは、シミュレーションや数値計算を乱数を発生させて行う手法。カジノで有名なモナコ公国の4つある地区の1つの名前に基づいている。
最後に
針を落として、その位置を観測するという単純な行動が、πという数学の世界の重要な数字や、モンテカルロ法という統計の世界で欠かせない手法と深く関わっているというのは、何とも面白い話ではないだろうか。
ビュフォンの針の問題は、針を平行線(等間隔の直線)が引かれた平面に落として、それが平行線に交わる確率を求める問題であるが、これを拡張して、例えば、同心円(半径が等間隔の円)が書かれた平面に落とした場合に、それが同心円に交わる確率はどうなるのか、さらには、等間隔の正方形が書かれた平面に落とした場合に、それが正方形と交わる確率はどうなるのか、といった問題を考えることもできる。
今やコンピューターを使えば、多数の試行を繰り返すことで、結果数値の概要を知ることは比較的容易にできるようになっていると思われるが、その結果を合理的に説明あるいは証明することは必ずしも容易ではない。このことは、過去の実験等に基づく観測値や経験則の説明のための理論構築に、多くの優秀な研究者等の多大な時間と労力が費やされていること、それでも未だ解決されていない問題が数多く存在している、ことが示している。
いずれにしても、単なるお遊びのように見えることでも、実は重要な法則等が含まれており、大きな発見につながっていくものである、ということを直に感じられるとしたら、それはそれで楽しいものではないかと思われるがいかがだろうか。
ビュフォンの針の問題は、針を平行線(等間隔の直線)が引かれた平面に落として、それが平行線に交わる確率を求める問題であるが、これを拡張して、例えば、同心円(半径が等間隔の円)が書かれた平面に落とした場合に、それが同心円に交わる確率はどうなるのか、さらには、等間隔の正方形が書かれた平面に落とした場合に、それが正方形と交わる確率はどうなるのか、といった問題を考えることもできる。
今やコンピューターを使えば、多数の試行を繰り返すことで、結果数値の概要を知ることは比較的容易にできるようになっていると思われるが、その結果を合理的に説明あるいは証明することは必ずしも容易ではない。このことは、過去の実験等に基づく観測値や経験則の説明のための理論構築に、多くの優秀な研究者等の多大な時間と労力が費やされていること、それでも未だ解決されていない問題が数多く存在している、ことが示している。
いずれにしても、単なるお遊びのように見えることでも、実は重要な法則等が含まれており、大きな発見につながっていくものである、ということを直に感じられるとしたら、それはそれで楽しいものではないかと思われるがいかがだろうか。
(2017年10月30日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月22日
高市新政権が発足、円相場の行方を考える~マーケット・カルテ11月号 -
2025年10月22日
貿易統計25年9月-米国向け自動車輸出が数量ベースで一段と落ち込む。7-9月期の外需寄与度は前期比▲0.4%程度のマイナスに -
2025年10月22日
米連邦地裁、Googleへの是正措置を公表~一般検索サービス市場における独占排除 -
2025年10月21日
選択と責任──消費社会の二重構造(2)-欲望について考える(3) -
2025年10月21日
連立協議から選挙のあり方を思う-選挙と同時に大規模な公的世論調査の実施を
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【円周率πが現われる世界-ビュフォンの針の問題-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
円周率πが現われる世界-ビュフォンの針の問題-のレポート Topへ


















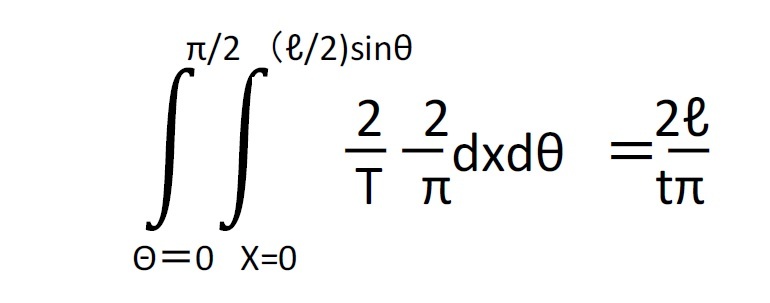
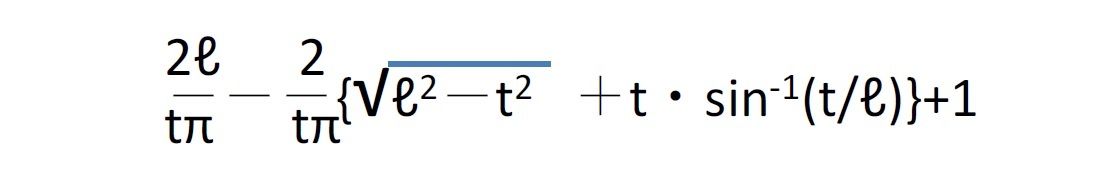

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




