- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「ほとんど整数」という概念-「ほとんど」何とか(1)-
コラム
2017年05月15日
文字サイズ
- 小
- 中
- 大
はじめに
皆さんは、「ほとんど整数」という言葉を聞いたことがあるだろうか。その名の通り、ほとんど整数に近いのだけれども、微妙に小数点以下が完全な0ではなくで、整数ではない数である。
なぜ、これが興味深いのかというと、一見しただけでは、通常はこんな数が「ほとんど整数」に近い数になるとは思われない数が、これに該当するからである。
それがどうした、というふうに思われるかもしれないが、興味深いと思われる人は、引き続きコラムを読んでいただきたい。
なぜ、これが興味深いのかというと、一見しただけでは、通常はこんな数が「ほとんど整数」に近い数になるとは思われない数が、これに該当するからである。
それがどうした、というふうに思われるかもしれないが、興味深いと思われる人は、引き続きコラムを読んでいただきたい。
ほとんど整数という概念
実は「ほとんど整数」に明確な定義があるわけではない。小数点以下に「0」や「9」がいくつ続けば「ほとんど整数」と呼んでいいのかは決まりがあるわけではない。英語では文字通り「Almost Integer」と表現されている。
「ほとんど整数」については、単なる数学のお遊びというわけでもなく、数学的な理論の裏付けがある場合もあるというから驚きである。
「ほとんど整数」については、単なる数学のお遊びというわけでもなく、数学的な理論の裏付けがある場合もあるというから驚きである。
ほとんど整数の具体例(その1)
例えば、以前の研究員の眼で紹介した、インドの数学の大天才シュリニヴァーサ・ラマヌジャン(Srinivasa Aiyengar Ramanujan)(1887~1920)は、いくつかの「ほとんど整数」を発見している。実際にはラマヌジャンが発見したわけでもないようだが、以下は、「ラマヌジャン定数」と呼ばれているようである。
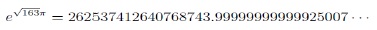
ここに、eはネイピア数(自然対数の底)で、πは円周率であり、
e = 2.71828 18284 59045 23536 02874 71352 …
π = 3.14159 26535 89793 23846 26433 83279 50288 …
と表される。
eもπもいわゆる無理数(分子・分母ともに整数である分数として表すことのできない実数)であるだけでなく、超越数(どんな有理係数の代数方程式の解にもならないような複素数)である。
このような数のべき乗がほとんど整数に近い数になるということは、何とも不思議な気持ちがするのではないか。
ただし、この数が整数に近い理由は、決して偶然ではなく、理論的に説明できるとのことである。東京電機大学の硲 文夫教授によれば、「その説明には『2 次体のイデアル類群の構造論』という代数学の理論、『楕円モジュラー関数論』という解析学の理論が使われる。」とのことである。
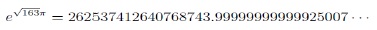
ここに、eはネイピア数(自然対数の底)で、πは円周率であり、
e = 2.71828 18284 59045 23536 02874 71352 …
π = 3.14159 26535 89793 23846 26433 83279 50288 …
と表される。
eもπもいわゆる無理数(分子・分母ともに整数である分数として表すことのできない実数)であるだけでなく、超越数(どんな有理係数の代数方程式の解にもならないような複素数)である。
このような数のべき乗がほとんど整数に近い数になるということは、何とも不思議な気持ちがするのではないか。
ただし、この数が整数に近い理由は、決して偶然ではなく、理論的に説明できるとのことである。東京電機大学の硲 文夫教授によれば、「その説明には『2 次体のイデアル類群の構造論』という代数学の理論、『楕円モジュラー関数論』という解析学の理論が使われる。」とのことである。
ほとんど整数の具体例(その2)
さらには、黄金数として知られるφ(ファイ)について、

等となっている。
これは、割と簡単にその仕組みを説明できる。
黄金数が表す黄金比とは、「線分をa, b の長さで 2 つに分割するときに、a : b = b : (a + b) が成り立つように分割したときの比 a : b 」(線分を2つに分割する時に、短い部分と長い部分との比が、長い部分と全体との比に等しくなる比率)のことであり、人間にとって最も安定し、美しい比率であるとされているものである。
a=1 とした場合を考えれば、黄金数は、2次方程式b2- b-1 = 0 の正の解となり、
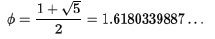
となる。従って、黄金数は無理数ではあるが、超越数ではない。
先の2次方程式のもう一つの解は、
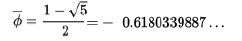
であるが、容易にわかるように、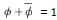 、
、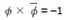 (これらを基本対称式と呼んでいる)となる。
(これらを基本対称式と呼んでいる)となる。
ここで、全ての対称式(変数を入れ替えても変わらない多項式)については、基本対称式を変数にとる整数係数多項式で表すことができる、という「対称式の基本定理」と呼ばれるものがある。これにより、対称式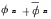 についても、基本対称式の整数係数多項式の結果として、整数となる。
についても、基本対称式の整数係数多項式の結果として、整数となる。
具体的には、例えば、以下のような感じである。
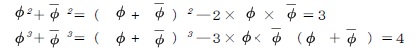
ここで、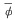 の絶対値は1より小さいため、
の絶対値は1より小さいため、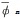 はnが大きくなると0に近づいていく。従って、 φn はnが大きくなると整数に近づいていくということになる。
はnが大きくなると0に近づいていく。従って、 φn はnが大きくなると整数に近づいていくということになる。
これを聞いてしまうと、「何だ、そういうことか」と思うかもしれない。

等となっている。
これは、割と簡単にその仕組みを説明できる。
黄金数が表す黄金比とは、「線分をa, b の長さで 2 つに分割するときに、a : b = b : (a + b) が成り立つように分割したときの比 a : b 」(線分を2つに分割する時に、短い部分と長い部分との比が、長い部分と全体との比に等しくなる比率)のことであり、人間にとって最も安定し、美しい比率であるとされているものである。
a=1 とした場合を考えれば、黄金数は、2次方程式b2- b-1 = 0 の正の解となり、
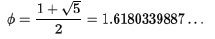
となる。従って、黄金数は無理数ではあるが、超越数ではない。
先の2次方程式のもう一つの解は、
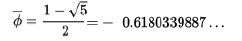
であるが、容易にわかるように、
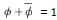 、
、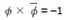 (これらを基本対称式と呼んでいる)となる。
(これらを基本対称式と呼んでいる)となる。ここで、全ての対称式(変数を入れ替えても変わらない多項式)については、基本対称式を変数にとる整数係数多項式で表すことができる、という「対称式の基本定理」と呼ばれるものがある。これにより、対称式
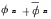 についても、基本対称式の整数係数多項式の結果として、整数となる。
についても、基本対称式の整数係数多項式の結果として、整数となる。具体的には、例えば、以下のような感じである。
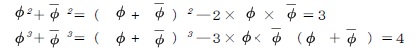
ここで、
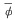 の絶対値は1より小さいため、
の絶対値は1より小さいため、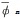 はnが大きくなると0に近づいていく。従って、 φn はnが大きくなると整数に近づいていくということになる。
はnが大きくなると0に近づいていく。従って、 φn はnが大きくなると整数に近づいていくということになる。これを聞いてしまうと、「何だ、そういうことか」と思うかもしれない。
ほとんど整数の具体例(その3)
ただし、全てがこのような形で合理的に説明できるわけではなさそうである。
例えば、
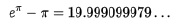
については、その理由の十分な説明はこれまでのところ発見されていないようである。
例えば、
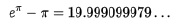
については、その理由の十分な説明はこれまでのところ発見されていないようである。
ほとんど整数となる理由
以上のように、ある複雑な算式で算出される数が、「ほとんど整数」になることについては、その合理的な理由が存在するものや、その説明が与えられておらず、単なる偶然と考えられているもの等様々なケースが存在しているようである。
因みに、循環十進小数と呼ばれる無限に9の続く無限小数「0.999... 」は、「ほとんど整数(に近い1)」ではなく、完全に1に等しい、のでお間違いのないように。
因みに、循環十進小数と呼ばれる無限に9の続く無限小数「0.999... 」は、「ほとんど整数(に近い1)」ではなく、完全に1に等しい、のでお間違いのないように。
最後に
すみません。このコラムを読んだ後、頭が「ほとんど真っ白」になってしまっている人がいたら、申し訳なく思っています。また、この面白さが「ほとんど理解不能」と思っている人がいることも「十分理解」できます。この点は悪しからず。
ただし、こうした趣味に近いようなことが、重要な奥深い数学的な理論に関係しているという事実は何となく楽しい気がするのではないかと思った次第です。
ただし、こうした趣味に近いようなことが、重要な奥深い数学的な理論に関係しているという事実は何となく楽しい気がするのではないかと思った次第です。
(2017年05月15日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「ほとんど整数」という概念-「ほとんど」何とか(1)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「ほとんど整数」という概念-「ほとんど」何とか(1)-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




