- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 円周率πが現われる世界(2)-互いに素となる確率-
コラム
2017年11月06日
文字サイズ
- 小
- 中
- 大
はじめに
「互いに素(coprime)」という概念については、学生時代に学んだので、多くの人が聞いたことがあるとの認識を有しているものと思われる。具体的には、「2つの整数aとbが互いに素である」とは、「a、bを共に割り切る正の整数が1のみである(aとbの最大公約数が1になる)」ことを言う。
今回は、この「互いに素」に関係して、円周率πが現われてくる世界を紹介する。
今回は、この「互いに素」に関係して、円周率πが現われてくる世界を紹介する。
互いに素となる確率
具体的には、任意に選ばれた2つの整数aとbがあるときに、このaとbが互いに素である確率を考える。その答えが6/π2(=0.607927…)となり、円周率πが現われることになる。
前回の研究員の眼と同様に、これについても、ここで円周率πが登場してくることについては、何とも不思議な感じがするのではないか。
前回の研究員の眼と同様に、これについても、ここで円周率πが登場してくることについては、何とも不思議な感じがするのではないか。
互いに素となる確率の証明
ζ(2)の値については、有名なスイスの数学者・天文学者であるレオンハルト・オイラー(Leonhard Euler)によって求められ、ζ(2)=π²/6 となっている。この証明をここで説明するのは紙面の都合上大変でもあるし、このコラムの意図するところでもないので、それは専門書等に委ねることにする。ただし、ここで円周率πが現われてくることについては、ゼータ関数ζ(s)の値を求める過程でsinXといった三角関数が使用されることと関係している、とだけ述べておく。πと三角関数の関係については、次回の研究員の眼で触れることにする。
いずれにしても、ここでは結果だけを引用させていただくことにして、求める確率は、
6/π²=0.607927…
となる。
aとbが偶数の場合には、互いに素ではないことから、それらのケースが全体の1/4あることを考えると、60.8%というのはかなり高い確率であると考えられる。
いずれにしても、ここでは結果だけを引用させていただくことにして、求める確率は、
6/π²=0.607927…
となる。
aとbが偶数の場合には、互いに素ではないことから、それらのケースが全体の1/4あることを考えると、60.8%というのはかなり高い確率であると考えられる。
3つ以上の整数が互いに素という概念とその確率
「互いに素」という概念は、3つ以上の整数に対しても拡張される。例えば、「3つの整数aとbとcが互いに素」であるとは、「aとbとcの最大公約数が1になる」ことをいう。これに対して、aとb、aとc、bとcが互いに素である場合には、「aとbとcは対ごとに素(pairwise coprime)」であるという。対ごとに素であれば互いに素となるが、互いに素であっても対ごとに素であるとは限らない(例:a =3、b = 5、c = 6)。あるいは、2つの数字が互いに素であれば、それらの2つの数字を含む3つの数字は互いに素となる。
任意に選んだk個の整数が互いに素である確率は、2つの数字の場合と同様の考え方により算出され、その結果は1/ζ(k) で表されることになる。具体的には、以下の通りとなる。
ζ(3)=1.20205… 1/ζ(3)=0.83190 …
ζ(4)=1.08232… (=π4/90 ) 1/ζ(4)=0.92393…
ζ(5)=1.03692… 1/ζ(5)=0.96438…
その定義から、当然のことながら、kが大きくなれば、それらが互いに素となる確率も大きくなっていく。
任意に選んだk個の整数が互いに素である確率は、2つの数字の場合と同様の考え方により算出され、その結果は1/ζ(k) で表されることになる。具体的には、以下の通りとなる。
ζ(3)=1.20205… 1/ζ(3)=0.83190 …
ζ(4)=1.08232… (=π4/90 ) 1/ζ(4)=0.92393…
ζ(5)=1.03692… 1/ζ(5)=0.96438…
その定義から、当然のことながら、kが大きくなれば、それらが互いに素となる確率も大きくなっていく。
互いに素となる数の性質
「互いに素」の概念については、例えば、以下の事実がある。
(1)異なる二つの素数pとqは互いに素であり、連続する二つの整数nと(n+1)も互いに素である。
(2)aとb が互いに素である時、2a − 1 と 2b − 1 も互いに素となる。
(3)aとb が互いに素である時、ax + by = 1 を満たす整数 x、y が存在する
(a、b、x、yは整数なのでマイナスの場合もあることに注意)
※ これは、ベズーの等式 (Bézout's identity)と呼ばれる初等整数論における定理の特別形である。ベズーの等式によれば、aとb を0でない整数とし、dをそれらの最大公約数とするとき、整数x とy が存在して、ax + by = d となる。xとy は (a, b) のベズー係数 (Bézout coefficients) と呼ばれる。それらは一意的ではない。ベズー係数の組は、拡張ユークリッドの互除法という手法によって計算できる。これについては、学生時代に学んでおり、大学の入学試験問題等に出されることもあるので、ご存知の方もおられると思う。
(1)異なる二つの素数pとqは互いに素であり、連続する二つの整数nと(n+1)も互いに素である。
(2)aとb が互いに素である時、2a − 1 と 2b − 1 も互いに素となる。
(3)aとb が互いに素である時、ax + by = 1 を満たす整数 x、y が存在する
(a、b、x、yは整数なのでマイナスの場合もあることに注意)
※ これは、ベズーの等式 (Bézout's identity)と呼ばれる初等整数論における定理の特別形である。ベズーの等式によれば、aとb を0でない整数とし、dをそれらの最大公約数とするとき、整数x とy が存在して、ax + by = d となる。xとy は (a, b) のベズー係数 (Bézout coefficients) と呼ばれる。それらは一意的ではない。ベズー係数の組は、拡張ユークリッドの互除法という手法によって計算できる。これについては、学生時代に学んでおり、大学の入学試験問題等に出されることもあるので、ご存知の方もおられると思う。
互いに素の概念の応用
「互いに素」となる整数は、上記の性質(3)により、RSA暗号(Rivest–Shamir–Adleman Cryptosystem)の秘密鍵の生成に利用されている。
RSA暗号とは、桁数が大きい合成数の素因数分解が困難であることから、それを安全性の根拠とした公開鍵暗号の一つである。その仕組みは、大まかに説明すると、以下の通りとなる。
(1)まずは、2つの素数pとqから、その積n=pq を求める。
(2)eとして、(p-1)(q-1)未満の正の整数で、(p-1)(q-1)と互いに素な数を選ぶ。
(3)次に、dを(p-1)(q-1)を法としたeの逆数とする。即ち、deを(p-1)(q-1)で割った余りが1(あるいは、(de-1)が(p-1)(q-1)の倍数)となるような数とする。
(4)この時、deを(p-1)(q-1)で割った時の整数部分の商(割り算の結果)をxとすれば、
de+(-x) (p-1)(q-1)=1 が成り立つ。
(5)これにより、nとeを公開鍵として、dを秘密鍵とすることができることになる。
巨大な素数pとq及びそれから得られる巨大な整数nを素数の積に分解することは、コンピューターを使用しても時間がかかる。従って、一般の人がこれを解明することは実際上不可能なことから、暗号化が可能になる。なお、この場合、pとqが漏れるとdが計算で求まることになるため、pとqは絶対に知られないようにしておく必要がある。
RSA暗号とは、桁数が大きい合成数の素因数分解が困難であることから、それを安全性の根拠とした公開鍵暗号の一つである。その仕組みは、大まかに説明すると、以下の通りとなる。
(1)まずは、2つの素数pとqから、その積n=pq を求める。
(2)eとして、(p-1)(q-1)未満の正の整数で、(p-1)(q-1)と互いに素な数を選ぶ。
(3)次に、dを(p-1)(q-1)を法としたeの逆数とする。即ち、deを(p-1)(q-1)で割った余りが1(あるいは、(de-1)が(p-1)(q-1)の倍数)となるような数とする。
(4)この時、deを(p-1)(q-1)で割った時の整数部分の商(割り算の結果)をxとすれば、
de+(-x) (p-1)(q-1)=1 が成り立つ。
(5)これにより、nとeを公開鍵として、dを秘密鍵とすることができることになる。
巨大な素数pとq及びそれから得られる巨大な整数nを素数の積に分解することは、コンピューターを使用しても時間がかかる。従って、一般の人がこれを解明することは実際上不可能なことから、暗号化が可能になる。なお、この場合、pとqが漏れるとdが計算で求まることになるため、pとqは絶対に知られないようにしておく必要がある。
最後に
学生時代に何となく学んだ「互いに素」という概念であるが、よくよく調べてみれば、なかなか面白い事実があり、実際の社会においても応用され役立っていることがわかる。
学校で、新しい概念や定義を学ぶ時には、それらが社会にどのように役立っており、どのような意味合いを有しているのか、について併せて教えていただければ、学ぶ者の興味もより一層深まっていくのではないか、と感じた次第である。
学校で、新しい概念や定義を学ぶ時には、それらが社会にどのように役立っており、どのような意味合いを有しているのか、について併せて教えていただければ、学ぶ者の興味もより一層深まっていくのではないか、と感じた次第である。
(2017年11月06日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【円周率πが現われる世界(2)-互いに素となる確率-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
円周率πが現われる世界(2)-互いに素となる確率-のレポート Topへ


















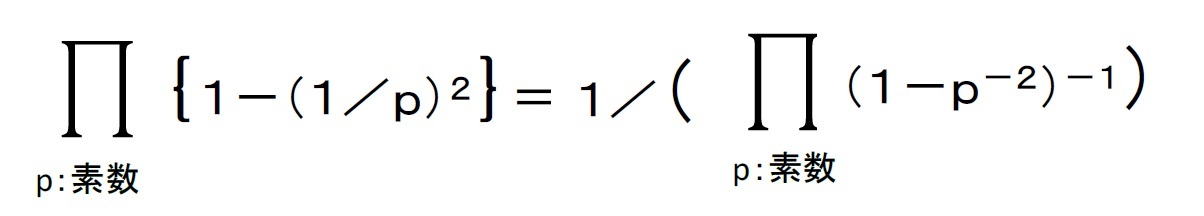
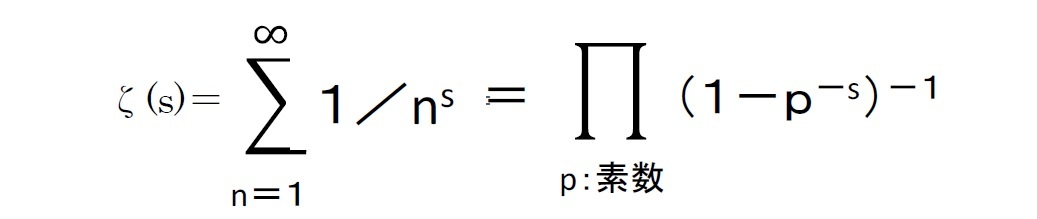

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




