- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 円周率πが現われる世界(3)-πが角度180°ってどういう意味-
コラム
2017年11月13日
文字サイズ
- 小
- 中
- 大
はじめに
π(パイ)と言えば、直径1の円の円周の長さを表す数値として、3.14という数値を思い浮かべる人が殆どだと思われるが、πが角度を表現するために使用される場合には180°を表している。これって何でと思う人もいるかもしれない。もちろん、学生時代に教えられているので十分ご承知の人も多いと思うが、今回はこれについて紹介する。
πは何で角度180°を表しているのか
答えは、πを角度を表すために使用する場合には、「度(°)」ではなくて、「ラジアン(radian)」という単位で表されているからである。
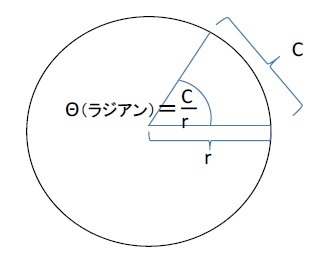
ラジアンとは、国際単位系における角度の単位であり、「1ラジアン」は「円の半径に等しい長さの弧の中心に対する角度」と定義される。1ラジアンは通常の「度数法」では、(180/π)°で、約57.29578°に相当することになる。
これにより、πラジアンは180°であり、2πラジアンが360°であり、(π/2)ラジアンが90°ということになる。
ラジアンについては、「弧度」とも言い、平面上の角度をラジアンで測る方式を「弧度法」と読んでいる。
ラジアンとは、国際単位系における角度の単位であり、「1ラジアン」は「円の半径に等しい長さの弧の中心に対する角度」と定義される。1ラジアンは通常の「度数法」では、(180/π)°で、約57.29578°に相当することになる。
これにより、πラジアンは180°であり、2πラジアンが360°であり、(π/2)ラジアンが90°ということになる。
ラジアンについては、「弧度」とも言い、平面上の角度をラジアンで測る方式を「弧度法」と読んでいる。
何故ラジアンが使用されるのか
しかも、これが必然的なものであればやむを得ないが、あくまでも角度の単位の定義によるものだとすれば、敢えて度数法を採用する意義は乏しいことになる。
また、ここでは示さないが、sinXとsinX°のグラフを比較してみれば、いかにラジアンをベースにすることが分かりやすく実用性の高いものになるのかが理解できる。
また、ここでは示さないが、sinXとsinX°のグラフを比較してみれば、いかにラジアンをベースにすることが分かりやすく実用性の高いものになるのかが理解できる。
弧度法と度数法
ところで、その定義から、「弧度法」による角度は、「半径の長さと弧の長さの比」で表される。2つの長さの比なので単位が打ち消しあってなくなることから単位はいらない、ということになるが、これに「ラジアン」という単位を付している。従って、ラジアンは無名数(bare number)として、単位を付さなくてもよい数として扱われる。
これに対して、「度数法」による角度は、なぜ1周が360°となるのか等について、もちろんその理由付けは行われているものの、必ずしも普遍性があるとはいえないものとなっている。このため、数学的に取り扱おうとすると、却って扱いにくいものとなってしまう。
なお、こうしたことは、物理の理論の世界でも同じであり、例えば、物理の円運動では角度はラジアンで扱われている。
なお、こうしたことは、物理の理論の世界でも同じであり、例えば、物理の円運動では角度はラジアンで扱われている。
角度の表示
角度も、他の長さや重量等の計量単位と同様に、人為的に定義されたものであり、我々が慣れ親しんでいる度数法はその1つの方法であるが、理論の世界では弧度法がより扱いやすいものとなっている。その意味で、基本的には日常生活では我々は弧度法を気にする必要はない。ただし、1点だけ、角度を表現する際には注意が必要になってくる。
会話においては、角度を表現するのに、ラジアンを使用する人はなく、通常度数法に基づく数値で「○○度」という言い方をしているので問題はない。ただし、文書で表現する場合には、一般的なルールとして、単に角度がθであると記述されている場合には、これはθラジアンを意味することになる。単位が付与されないのは、先に述べたように、弧度法による角度が比を表しているからである。一方で、度数法で表現する場合には、それが人為的に設定されたものからきていることから、必ず「°」を数字の後に付けなければならないことになる。
会話においては、角度を表現するのに、ラジアンを使用する人はなく、通常度数法に基づく数値で「○○度」という言い方をしているので問題はない。ただし、文書で表現する場合には、一般的なルールとして、単に角度がθであると記述されている場合には、これはθラジアンを意味することになる。単位が付与されないのは、先に述べたように、弧度法による角度が比を表しているからである。一方で、度数法で表現する場合には、それが人為的に設定されたものからきていることから、必ず「°」を数字の後に付けなければならないことになる。
最後に
以上、弧度法というものが、自然な考え方から生まれてきているものであり、その方式に基づけば、結果的にπラジアンというのが180°というきりのよい角度になり、各種の理論的な分析を扱いやすいものとすることに貢献していることを紹介してきた。ここにおいて、πが重要な役割を果たしていることがご理解いただけたと思う。
また1つ、πという数字の持つ特別な意味合いとその重要性が見えてきたような気がするのではないか。
また1つ、πという数字の持つ特別な意味合いとその重要性が見えてきたような気がするのではないか。
(2017年11月13日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月29日
生活習慣病リスクを高める飲酒の現状と改善に向けた対策~男女の飲酒習慣の違いに着目して -
2025年10月29日
地域イベントの現実と課題-渋谷のハロウィンをイベントとして運営できるか- -
2025年10月28日
試練の5年に踏み出す中国(前編)-「第15次五カ年計画」の5年間は、どのような5年か -
2025年10月28日
地域医療連携推進法人の現状と今後を考える-「連携以上、統合未満」で協力する形態、その将来像は? -
2025年10月28日
東宝の自己株式取得-公開買付による取得
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【円周率πが現われる世界(3)-πが角度180°ってどういう意味-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
円周率πが現われる世界(3)-πが角度180°ってどういう意味-のレポート Topへ


















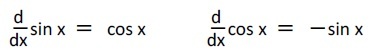
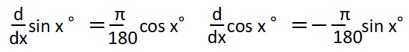
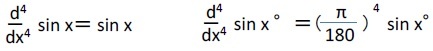

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




