- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無限について-無限に関するパラドックス(1)-
コラム
2022年06月17日
文字サイズ
- 小
- 中
- 大
はじめに
ゼノンのパラドックス-アキレスと亀
「ゼノンのパラドックス」あるいは「ゼノンの逆説」と呼ばれているものは、古代ギリシャの自然哲学者であるエレアのゼノン(Zeno of Elea)が唱えたパラドックスである。
それにはいくつかのものがあるが、最も有名なものの1つは「アキレスと亀」に関するものである。これは、「(古代ギリシャ随一のスプリンターとして知られる)アキレスと亀が100m 競争をする。ただし、アキレスにはハンディキャップが与えられて、亀は50m先からスタートする。この時、アキレスが亀のいる地点に到着した時には亀は先に進んでおり、さらにアキレスが亀の進んだ先に到着した時には亀はさらに先に進んでいる。このことが繰り返されるため、アキレスはいつまで経っても亀には追い付けない。」というものである。
これは明らかにおかしい。アキレスは亀に追いついて、さらには追い越していくことは誰が考えても明らかである。ところが、何故このゼノンの考え方がおかしいのか、何が間違っているのかを説明せよと言われると、はたと困ってしまう人が多いものと思われる。
数学の問題としては、アキレスと亀の速度が与えられれば、どの時点で追いつくことができるのかを簡単に計算することができる。それでも、それでは「ゼノンのパラドックス」の誤りを直接的に指摘したことにはなっていない。従って、何かもやもやしたものが残ってしまい、歯痒い気持ちになってしまうのではないだろうか。
というわけで、この考え方が誤っている点を説明すると、それは「『アキレスが亀に追いつくまでに亀が先に進んでいる』というプロセスが無限に繰り返されることから、いつまで経っても(即ち、無限の時間をかけても)追いつかない。」としている点にある。つまり、「アキレスが亀に追いつくまでに亀が先に進んでいる」というプロセスは確かに無限に繰り返すことができるかもしれないが、このプロセスは結局はある一定の有限の時間内でしか行われない。即ち、その有限の時間に到達すると、アキレスは亀に追いついて、さらにその時間を過ぎると、アキレスは亀を追い越していくことになる。つまり、この考え方の誤りは、「無限の回数が無限の時間で行われる」かのような論理を展開している点にあることになる。
このパラドックスの背景には、「無限個の数の足し算(無限和)が有限に収束する」ケースがあるという事実があり、このことを指摘することがなかなか難しいという点があったようだ。
これに類似したパラドックスに「弾むボールは永久に止まらない」というものがある。これは「ボールをある高さから落下させた場合に、床で弾んで半分の高さまで跳ね返るとする。これが繰り返されるため、このボールは永久に止まらない。」というものである。これについても、同様の考え方で、「無限回、弾むかもしれないが、その弾んでいる時間は有限な値に収束する。」ので、その時間にはボールは静止する、ことになる。
それにはいくつかのものがあるが、最も有名なものの1つは「アキレスと亀」に関するものである。これは、「(古代ギリシャ随一のスプリンターとして知られる)アキレスと亀が100m 競争をする。ただし、アキレスにはハンディキャップが与えられて、亀は50m先からスタートする。この時、アキレスが亀のいる地点に到着した時には亀は先に進んでおり、さらにアキレスが亀の進んだ先に到着した時には亀はさらに先に進んでいる。このことが繰り返されるため、アキレスはいつまで経っても亀には追い付けない。」というものである。
これは明らかにおかしい。アキレスは亀に追いついて、さらには追い越していくことは誰が考えても明らかである。ところが、何故このゼノンの考え方がおかしいのか、何が間違っているのかを説明せよと言われると、はたと困ってしまう人が多いものと思われる。
数学の問題としては、アキレスと亀の速度が与えられれば、どの時点で追いつくことができるのかを簡単に計算することができる。それでも、それでは「ゼノンのパラドックス」の誤りを直接的に指摘したことにはなっていない。従って、何かもやもやしたものが残ってしまい、歯痒い気持ちになってしまうのではないだろうか。
というわけで、この考え方が誤っている点を説明すると、それは「『アキレスが亀に追いつくまでに亀が先に進んでいる』というプロセスが無限に繰り返されることから、いつまで経っても(即ち、無限の時間をかけても)追いつかない。」としている点にある。つまり、「アキレスが亀に追いつくまでに亀が先に進んでいる」というプロセスは確かに無限に繰り返すことができるかもしれないが、このプロセスは結局はある一定の有限の時間内でしか行われない。即ち、その有限の時間に到達すると、アキレスは亀に追いついて、さらにその時間を過ぎると、アキレスは亀を追い越していくことになる。つまり、この考え方の誤りは、「無限の回数が無限の時間で行われる」かのような論理を展開している点にあることになる。
このパラドックスの背景には、「無限個の数の足し算(無限和)が有限に収束する」ケースがあるという事実があり、このことを指摘することがなかなか難しいという点があったようだ。
これに類似したパラドックスに「弾むボールは永久に止まらない」というものがある。これは「ボールをある高さから落下させた場合に、床で弾んで半分の高さまで跳ね返るとする。これが繰り返されるため、このボールは永久に止まらない。」というものである。これについても、同様の考え方で、「無限回、弾むかもしれないが、その弾んでいる時間は有限な値に収束する。」ので、その時間にはボールは静止する、ことになる。
ゼノンのパラドックス-飛んでいる矢は止まっている
「ゼノンのパラドックス」で次に有名なのは、「飛んでいる矢は止まっている」というものである。これは、「飛んでいる矢は、いつの時点でもその瞬間は止まっている。いつの時点でもその瞬間に止まっているならば, いつも止まっているわけだから、矢は止まっていて動かない。」というものである。
これに対する明確な回答を得るには、微分積分の考え方が生まれてくるまでの時間を要している。
即ち、「瞬間」という言葉の意味するところが重要であり、これが「0」を意味しているのであれば、まさしく「0」からは「0」にしかならないということになってしまう。実は「瞬間」というのを、「極めて短い時間Δtを想定して、このΔtを限りなく0に近づけた極限」として定義することにより、飛んでいる矢は、「各瞬間において、いわゆる速度を有しており、動いている」ということになる。これにより、時間とともに矢は飛んでいく、ことになる。
これに対する明確な回答を得るには、微分積分の考え方が生まれてくるまでの時間を要している。
即ち、「瞬間」という言葉の意味するところが重要であり、これが「0」を意味しているのであれば、まさしく「0」からは「0」にしかならないということになってしまう。実は「瞬間」というのを、「極めて短い時間Δtを想定して、このΔtを限りなく0に近づけた極限」として定義することにより、飛んでいる矢は、「各瞬間において、いわゆる速度を有しており、動いている」ということになる。これにより、時間とともに矢は飛んでいく、ことになる。
二分法のパラドックス
「二分法(dichotomy)」というのは、ある意味で、先の「アキレスと亀」のパラドックスの論法に似ている。(厳密ではないが)「アキレスと亀」のパラドックスが、この二分法の進化版、あるいは1つの具体例と言う言い方もできるかもしれない。
これは、「ある地点に到達するためには、その半分の中間点に到達しなければならない。さらにその中間点に到達するためには、その中間点までの半分に到達しなければならない。この論法を繰り返していくと、結局いつまでたっても最初の目標地点には到達できない、ということになる、というパラドックスである。
これも、距離を無限に分割して、その距離に到達するまでの時間を無限に分割していっても、結局はそれらの無限の時間の累計は有限の時間となり、有限の時間で目標の地点に到達することができることになり、その時間を過ぎれば、中間点等を通過して、さらに先に進むことができることになる。
即ち、このパラドックスもまさに、「無限の距離の分割により、運動が無限の時間で行われる」かのような論理を展開している点に問題がある。
これは、「ある地点に到達するためには、その半分の中間点に到達しなければならない。さらにその中間点に到達するためには、その中間点までの半分に到達しなければならない。この論法を繰り返していくと、結局いつまでたっても最初の目標地点には到達できない、ということになる、というパラドックスである。
これも、距離を無限に分割して、その距離に到達するまでの時間を無限に分割していっても、結局はそれらの無限の時間の累計は有限の時間となり、有限の時間で目標の地点に到達することができることになり、その時間を過ぎれば、中間点等を通過して、さらに先に進むことができることになる。
即ち、このパラドックスもまさに、「無限の距離の分割により、運動が無限の時間で行われる」かのような論理を展開している点に問題がある。
有限と無限の関係
今回のパラドックスが意味していることは、「有限」と「無限」の関係を正しく理解し、極限の概念を明確にしていかなければならない、ということにある。
有限のものを無限に分割することができても、それはあくまでも対象となる有限なものを無限に分割することができる(例えば、直線を無限に分割していくができる)ということであり、その無限に分割されていったことで、元々目指していたものを達するために要するもの(例えば、時間)も無限に小さくなっていくことになる。結果として、元々有限のものが無限になるということではないし、元々の有限のものに対応して、目指すべきものが有限の範囲内で到達されていく、ということには何らの影響も与えないということになる。
ある意味で、2つの全く異なること((1)有限のものを無限に分割できる、(2)有限のものを有限の時間等で達成できる)をいかにも両者が密接に深く関係しているかのような論理を展開していることに問題があることになる。
有限のものを無限に分割することができても、それはあくまでも対象となる有限なものを無限に分割することができる(例えば、直線を無限に分割していくができる)ということであり、その無限に分割されていったことで、元々目指していたものを達するために要するもの(例えば、時間)も無限に小さくなっていくことになる。結果として、元々有限のものが無限になるということではないし、元々の有限のものに対応して、目指すべきものが有限の範囲内で到達されていく、ということには何らの影響も与えないということになる。
ある意味で、2つの全く異なること((1)有限のものを無限に分割できる、(2)有限のものを有限の時間等で達成できる)をいかにも両者が密接に深く関係しているかのような論理を展開していることに問題があることになる。
(参考)実無限と可能無限
と表した場合には、これは収束する特定の数を表すことになるので、実無限に則ったものとなる。
なお、ここで現れてくる無限大を表す記号「∞」自体が、「実無限」の考え方によるものとなる。
今回紹介した「アキレスと亀」のようなパラドックスは、まさに可能無限の考え方に則った視点に基づいたものとなっている。これに対して、その誤りを指摘する説明は、実無限の考え方に則った視点に基づくものとなっている、と言えるだろう。
数学の世界では、基本的には「実無限」の考え方に基づいて論理が展開されているので、今回を含めて、今後の無限に関する研究員の眼のシリーズでは、基本的には「実無限」の考え方をベースに記述していくことにする。
なお、ここで現れてくる無限大を表す記号「∞」自体が、「実無限」の考え方によるものとなる。
今回紹介した「アキレスと亀」のようなパラドックスは、まさに可能無限の考え方に則った視点に基づいたものとなっている。これに対して、その誤りを指摘する説明は、実無限の考え方に則った視点に基づくものとなっている、と言えるだろう。
数学の世界では、基本的には「実無限」の考え方に基づいて論理が展開されているので、今回を含めて、今後の無限に関する研究員の眼のシリーズでは、基本的には「実無限」の考え方をベースに記述していくことにする。
最後に
今回は、有限と無限の関係についての理解を深めるために、ゼノンのパラドックスのいくつかについて紹介してきた。
有限と無限の関係については、単純な数学的な思考だけでなく、哲学的な思考を要する面があり、非常に興味深い話題である。ただし、これに深入りしすぎると、寝食を忘れて没頭してしまうということにもなりかねない。その意味では、こんなトピックもあるのだな、程度に思っていただければよいのではないかと思われる。
有限と無限の関係については、単純な数学的な思考だけでなく、哲学的な思考を要する面があり、非常に興味深い話題である。ただし、これに深入りしすぎると、寝食を忘れて没頭してしまうということにもなりかねない。その意味では、こんなトピックもあるのだな、程度に思っていただければよいのではないかと思われる。
(2022年06月17日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月22日
高市新政権が発足、円相場の行方を考える~マーケット・カルテ11月号 -
2025年10月22日
貿易統計25年9月-米国向け自動車輸出が数量ベースで一段と落ち込む。7-9月期の外需寄与度は前期比▲0.4%程度のマイナスに -
2025年10月22日
米連邦地裁、Googleへの是正措置を公表~一般検索サービス市場における独占排除 -
2025年10月21日
選択と責任──消費社会の二重構造(2)-欲望について考える(3) -
2025年10月21日
連立協議から選挙のあり方を思う-選挙と同時に大規模な公的世論調査の実施を
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無限について-無限に関するパラドックス(1)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無限について-無限に関するパラドックス(1)-のレポート Topへ



















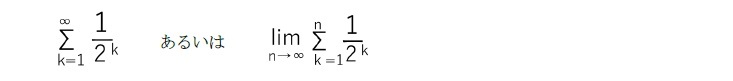

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




