- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無理数について(その2)-無理数の(有理数や無理数)べき乗や無理数度等-
コラム
2021年12月13日
文字サイズ
- 小
- 中
- 大
はじめに
無理数に関する話題について、複数回に分けて紹介している。前回の研究員の眼では、無理数の定義と無理数同士や有理数との四則演算結果等について紹介した。
今回の研究員の眼では、「無理数の(無理数や有理数)べき乗」、「無理数度」及び「2次無理数と連分数展開」について紹介する。
今回の研究員の眼では、「無理数の(無理数や有理数)べき乗」、「無理数度」及び「2次無理数と連分数展開」について紹介する。
ここで、log25 が無理数であることは、以下のように背理法で証明される。
(証明)log25 が有理数であるとすると、互いに素な自然数pとqを用いて、log25=q/pと表されることから、対数の定義により 2q/p=5 、両辺をp乗すると 2q=5p となるが、これは素因数分解の一意性に反する。
なお、同様に背理法により、例えば、aとbが互いに素な自然数の場合、logab は無理数となることが証明される。
(証明)log25 が有理数であるとすると、互いに素な自然数pとqを用いて、log25=q/pと表されることから、対数の定義により 2q/p=5 、両辺をp乗すると 2q=5p となるが、これは素因数分解の一意性に反する。
なお、同様に背理法により、例えば、aとbが互いに素な自然数の場合、logab は無理数となることが証明される。
一方で、「(正の)無理数の累乗根は無理数」となる。
これも、無理数aのn乗根n√aが有理数になると、これらのn乗の(n√a)n(=a)も有理数となってしまい、矛盾することから明らかである。
これも、無理数aのn乗根n√aが有理数になると、これらのn乗の(n√a)n(=a)も有理数となってしまい、矛盾することから明らかである。
無理数の無理数乗
上記算式により、少なくとも「無理数の無理数乗で有理数になる例が存在する」ことが示されている。
というのも、中間結果である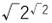 が有理数であるか無理数であるかはわからなくても、もしこれが有理数であればそれが具体例となるし、もしそうでなければこの無理数の√2乗が2となっていることから、これが具体例になるからである。
が有理数であるか無理数であるかはわからなくても、もしこれが有理数であればそれが具体例となるし、もしそうでなければこの無理数の√2乗が2となっていることから、これが具体例になるからである。
実際には、「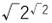 は無理数かつ超越数である」ことが証明されている。これは「α を 0、1 以外の代数的数、β を有理数ではない代数的数としたとき、αβは超越数である。」という「ゲルフォント=シュナイダーの定理」の一つの具体例に該当するものになっている。
は無理数かつ超越数である」ことが証明されている。これは「α を 0、1 以外の代数的数、β を有理数ではない代数的数としたとき、αβは超越数である。」という「ゲルフォント=シュナイダーの定理」の一つの具体例に該当するものになっている。
なお、この定理は、有名なドイツの数学者であるダフィット・ヒルベルト(David Hilbert)によりまとめられた当時未解決だった23の数学問題である「ヒルベルトの23の問題」の7番目の問題を解決するもので、ヒルベルトが大変難しい問題と考えていたものだった。
8番目の問題が有名な「リーマン予想」で、1928年の講演で、ヒルベルト自身は、リーマン予想は自分が存命中に解決するが、7番目の問題は講演参加者の存命中は解決されないだろう、と述べていたと言われている。ところが、実際には、この7番目の問題が1934年に、ソ連の数学者であるアレクサンダー・ゲルフォント(Alexander Gelfond)とドイツの数学者であるテオドール・シュナイダー(Theodor Schneider)によって、それぞれ独立に証明された一方で、リーマン予想は未だ解決されておらず、数学における最も重要な未解決問題の1つになっている。
大数学者といえども、将来を予測することは難しいことがわかる。
というのも、中間結果である
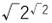 が有理数であるか無理数であるかはわからなくても、もしこれが有理数であればそれが具体例となるし、もしそうでなければこの無理数の√2乗が2となっていることから、これが具体例になるからである。
が有理数であるか無理数であるかはわからなくても、もしこれが有理数であればそれが具体例となるし、もしそうでなければこの無理数の√2乗が2となっていることから、これが具体例になるからである。実際には、「
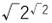 は無理数かつ超越数である」ことが証明されている。これは「α を 0、1 以外の代数的数、β を有理数ではない代数的数としたとき、αβは超越数である。」という「ゲルフォント=シュナイダーの定理」の一つの具体例に該当するものになっている。
は無理数かつ超越数である」ことが証明されている。これは「α を 0、1 以外の代数的数、β を有理数ではない代数的数としたとき、αβは超越数である。」という「ゲルフォント=シュナイダーの定理」の一つの具体例に該当するものになっている。なお、この定理は、有名なドイツの数学者であるダフィット・ヒルベルト(David Hilbert)によりまとめられた当時未解決だった23の数学問題である「ヒルベルトの23の問題」の7番目の問題を解決するもので、ヒルベルトが大変難しい問題と考えていたものだった。
8番目の問題が有名な「リーマン予想」で、1928年の講演で、ヒルベルト自身は、リーマン予想は自分が存命中に解決するが、7番目の問題は講演参加者の存命中は解決されないだろう、と述べていたと言われている。ところが、実際には、この7番目の問題が1934年に、ソ連の数学者であるアレクサンダー・ゲルフォント(Alexander Gelfond)とドイツの数学者であるテオドール・シュナイダー(Theodor Schneider)によって、それぞれ独立に証明された一方で、リーマン予想は未だ解決されておらず、数学における最も重要な未解決問題の1つになっている。
大数学者といえども、将来を予測することは難しいことがわかる。
無理数の無理数乗(特殊なケース)
前回の研究員の眼で「代表的な無理数かつ超越数であるe(ネイピア数)とπ(円周率)について、その和や積であるe+πやe・πが有理数なのか、無理数なのかは証明されていない。」と紹介した。それでは、これらのべき乗である、eπ、ee、ππ、πe は有理数なのか、無理数なのか、はたして超越数なのだろうか。
これについても多くの人は、当然、無理数であり、超越数であろうと考えるのではないかと思われる。ところが、その結果については、「eπ(=(-1)―i )」は、「ゲルフォントの定数」と呼ばれる数学定数で、超越数である。」ことが分かっているが、ee、ππ、πe は有理数であるのか無理数であるのか超越数であるのか否かは証明されていない。
一方で、これらより若干複雑ではないかとの感じを受けるかもしれないπ+eπやπ・eπは超越数であることが証明されている。
これについても多くの人は、当然、無理数であり、超越数であろうと考えるのではないかと思われる。ところが、その結果については、「eπ(=(-1)―i )」は、「ゲルフォントの定数」と呼ばれる数学定数で、超越数である。」ことが分かっているが、ee、ππ、πe は有理数であるのか無理数であるのか超越数であるのか否かは証明されていない。
一方で、これらより若干複雑ではないかとの感じを受けるかもしれないπ+eπやπ・eπは超越数であることが証明されている。
無理数度
無理数について、その無理数としてのレベルに階層があり、それを図る指標として「無理数度」という尺度がある。
これは、ある数αに対して、
|α-p/q|<1/qκ
を満たす有理数p/qが有限個しかない、という性質を満たすκの下限のことを指しており、これをαの「無理数度(irrationality measure)」という。
その定義により、有理数の無理数度は1となる。また、ディリクレの定理と呼ばれるものにより、全ての無理数の無理数度は2以上となる。さらに、ロスの定理と呼ばれるものにより、代数的無理数の無理数度は2となるが逆はいえない。
超越数でも、eの無理数度は2となっている。これに対して、πの無理数度は8.016045…… となっている。
さらには、「リウヴィル数(Liouville number)」と呼ばれるものの無理数度は∞(無限大)となっている。
リウヴィル数というのは、以下の定義を満たす実数 α のことである
「 任意の正整数 n に対して、
0<|α-p/q|<1/qn
を満たす有理数 p/q (q > 1) が少なくとも一つ存在する。 」
これは、ある数αに対して、
|α-p/q|<1/qκ
を満たす有理数p/qが有限個しかない、という性質を満たすκの下限のことを指しており、これをαの「無理数度(irrationality measure)」という。
その定義により、有理数の無理数度は1となる。また、ディリクレの定理と呼ばれるものにより、全ての無理数の無理数度は2以上となる。さらに、ロスの定理と呼ばれるものにより、代数的無理数の無理数度は2となるが逆はいえない。
超越数でも、eの無理数度は2となっている。これに対して、πの無理数度は8.016045…… となっている。
さらには、「リウヴィル数(Liouville number)」と呼ばれるものの無理数度は∞(無限大)となっている。
リウヴィル数というのは、以下の定義を満たす実数 α のことである
「 任意の正整数 n に対して、
0<|α-p/q|<1/qn
を満たす有理数 p/q (q > 1) が少なくとも一つ存在する。 」
は、リウヴィル数である。この数は、1844年に、リウヴィルによって、超越数であることが証明され、超越数の存在が初めて示されたものとなった。
ジョゼフ・リウヴィル(Joseph Liouville)は、フランスの数学者で物理学者であり、物理学、解析学、数論の3つの分野で「リウヴィルの定理」と呼ばれる業績を残している。
ジョゼフ・リウヴィル(Joseph Liouville)は、フランスの数学者で物理学者であり、物理学、解析学、数論の3つの分野で「リウヴィルの定理」と呼ばれる業績を残している。
2次無理数と連分数展開
ここで a0 は整数、それ以外の an は正の整数である。
ある数をこのような連分数で表すことを「連分数展開」と呼んでいる。また、連分数展開を行ったときに、上記に現れるanが循環した数列になる場合、「循環連分数」という。
と、ここまで定義を述べてきたが、実は「2次無理数の正則連分数展開は必ず循環し、逆に、正則連分数展開が循環する数は2次無理数である。」ことが知られている。このことは、18世紀のフランスの大数学者であるジョゼフ=ルイ・ラグランジュ(Joseph-Louis Lagrange )によって証明されている。
これにより、無理数は、「連分数表示が循環連分数となる2次無理数」と「連分数表示が循環しない連分数となる2次でない無理数」に分類されることになる。
因みに、√2は、2次方程式x2 −2 = 0 の解で、以下のように連分数展開される2次無理数である。
ある数をこのような連分数で表すことを「連分数展開」と呼んでいる。また、連分数展開を行ったときに、上記に現れるanが循環した数列になる場合、「循環連分数」という。
と、ここまで定義を述べてきたが、実は「2次無理数の正則連分数展開は必ず循環し、逆に、正則連分数展開が循環する数は2次無理数である。」ことが知られている。このことは、18世紀のフランスの大数学者であるジョゼフ=ルイ・ラグランジュ(Joseph-Louis Lagrange )によって証明されている。
これにより、無理数は、「連分数表示が循環連分数となる2次無理数」と「連分数表示が循環しない連分数となる2次でない無理数」に分類されることになる。
因みに、√2は、2次方程式x2 −2 = 0 の解で、以下のように連分数展開される2次無理数である。
また、黄金数φも、以前の研究員の眼「黄金比φについて(その1)-黄金比とはどのようなものなのか-」(2020.11.10)で述べたように、2次方程式 x2 − x − 1 = 0 の正の解となり、以下のように連分数表示される2次無理数である。
繰り返しになるが、πやeは超越数なので、2次無理数ではない。また、eの無理数度は2だが、2次無理数ではない。
最後に
今回は、「無理数の(無理数や有理数)べき乗」、「無理数度」及び「2次無理数と連分数展開」について紹介した。
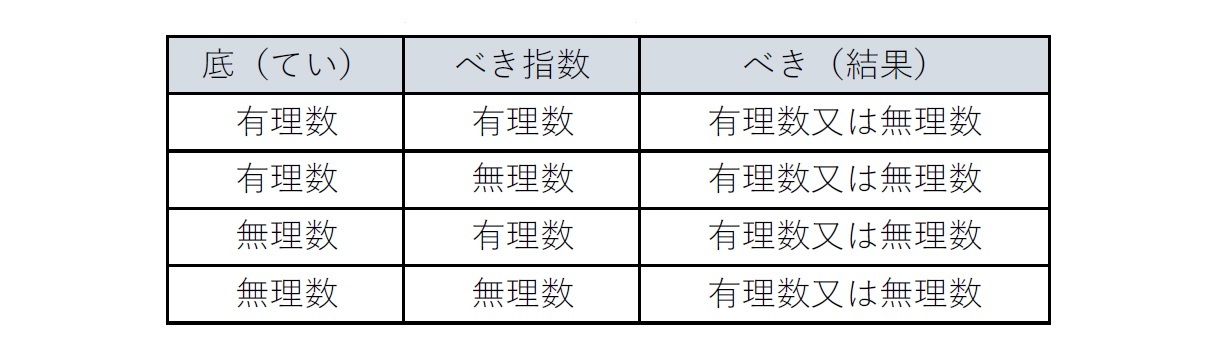
有理数と無理数の有理数乗や無理数乗が、いずれのケースにおいても、それほど自明ではないと思われるケースにおいても、有理数にも無理数にもなりうるという事実は、初めて聞くと少しは驚かれるのではないかと思われる。その定義等から考えた場合には、そういう結果になるのが自然だと認識できる場合もあるかもしれないが、ただ単に算式記号だけを見ていると、何となく不思議に思われるのではないだろうか。
また、無理数といっても、それには「無理性(?)の程度」があることを紹介した。
次回の研究員の眼では、具体的に無理数がどのようなところに現れてくるのかについて紹介する。これにより、無理数にさらに親近感を抱いていただければと思っている。
有理数と無理数の有理数乗や無理数乗が、いずれのケースにおいても、それほど自明ではないと思われるケースにおいても、有理数にも無理数にもなりうるという事実は、初めて聞くと少しは驚かれるのではないかと思われる。その定義等から考えた場合には、そういう結果になるのが自然だと認識できる場合もあるかもしれないが、ただ単に算式記号だけを見ていると、何となく不思議に思われるのではないだろうか。
また、無理数といっても、それには「無理性(?)の程度」があることを紹介した。
次回の研究員の眼では、具体的に無理数がどのようなところに現れてくるのかについて紹介する。これにより、無理数にさらに親近感を抱いていただければと思っている。
(2021年12月13日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無理数について(その2)-無理数の(有理数や無理数)べき乗や無理数度等-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無理数について(その2)-無理数の(有理数や無理数)べき乗や無理数度等-のレポート Topへ






















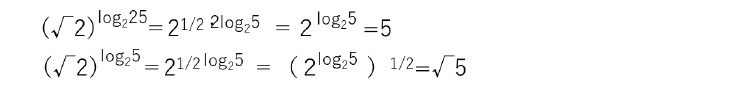
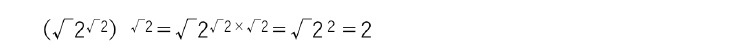
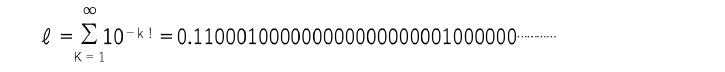





 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




