- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 巨大数について(その2)-ハイパー演算、各種の表記法等-
コラム
2022年02月16日
文字サイズ
- 小
- 中
- 大
はじめに
今回は「巨大数」(huge number)について何回かに分けて説明している。
前回の研究員の眼では、数詞で表現される巨大数(あるいは巨大な数を表す数詞)を中心に、我々が通常、感覚的に認識可能で、指数関数で表現できるような巨大数について紹介した。
今回の研究員の眼では、数詞では表現されないさらなる巨大数を表現するために、四則演算やべき乗等の演算を一般化した「ハイパー演算」の概念や各種の表記法等について紹介したい。
前回の研究員の眼では、数詞で表現される巨大数(あるいは巨大な数を表す数詞)を中心に、我々が通常、感覚的に認識可能で、指数関数で表現できるような巨大数について紹介した。
今回の研究員の眼では、数詞では表現されないさらなる巨大数を表現するために、四則演算やべき乗等の演算を一般化した「ハイパー演算」の概念や各種の表記法等について紹介したい。
ハイパー演算-既存の演算の表現-
「ハイパー演算(hyper operation)」というのは、は、加算、乗算、べき乗等の演算を一般化した演算のことを言う。またその演算のための演算子を「ハイパー演算子(hyper operator)」と呼んでいる。具体的には、これまでの加算、乗算、べき乗については、加算演算子をa + b = a (1)b、乗算演算子をab = a (2)b、冪乗演算子をab = a (3)bで表し、これを一般の非負整数nに一般化して、a (n) b とした形の演算子となっている。
これを関数形式で表すと、hyper1が加算、hyper2が乗算、hyper3が冪乗を表すことになり、以下の通りとなる。なお、hyper0は、第2被演算子と呼ばれるbの後者関数(即ちb+1)となる。
具体的には、以下の通りである。
これを関数形式で表すと、hyper1が加算、hyper2が乗算、hyper3が冪乗を表すことになり、以下の通りとなる。なお、hyper0は、第2被演算子と呼ばれるbの後者関数(即ちb+1)となる。
具体的には、以下の通りである。
ハイパー演算-テトレーション(n=4の場合)
この例からわかるように、これがとんでもなく大きな数を表していることが分かる。
前回の研究員の眼で紹介した「宇宙論で登場した最大の数」は、上記の表記方法によれば、
510<宇宙論で登場した最大の数<610
の範囲内にあることになる。
前回の研究員の眼で紹介した「宇宙論で登場した最大の数」は、上記の表記方法によれば、
510<宇宙論で登場した最大の数<610
の範囲内にあることになる。
また、n=5の時が「ペンテーション(pentation)」、n=6の時が「ヘキセーション(hexation)」等と呼ばれていき、演算が一般化されていくことになる。
クヌースの矢印表記
なお、クヌースの矢印は右結合で、a↑b↑c は、a↑(b↑c)を意味しており、(a↑b)↑c ではない。両者の結果は異なってくるので注意が必要となる。
また、先のハイパー演算子とは異なり、積・和・後者関数は表せない。
なお、矢印のかわりにサーカムフレックス(^)を使用して、a^^b のように表記するともあり、これは指数表記abがa^b と表現されることに準じている。
また、先のハイパー演算子とは異なり、積・和・後者関数は表せない。
なお、矢印のかわりにサーカムフレックス(^)を使用して、a^^b のように表記するともあり、これは指数表記abがa^b と表現されることに準じている。
コンウェイのチェーン表記
グラハム数
「グラハム数(Graham's number)」は、米国の数学者であるロナルド・グラハム(Ronald Graham)によって、ラムゼー理論に関する未解決問題の解の推定値の上限として得られた自然数で、数学の証明で使われたことのある最大の数として1980年にギネスブックに認められたことで知られている。即ち、巨大な数を作成することを意図して作られたものではなくて、実際の証明の過程で必然的に生まれてきたものとなっている。
グラハムとブルース・リー・ロスチャイルド(Bruce Lee Rothschild)による「グラハムの定理」は、「n 次元超立方体の 2n 個の頂点のそれぞれを互いに全て線で結ぶ。次に2つの色を用いて連結した線をいずれかの色に塗り分ける。このとき n が十分大きければ、どんな塗り方をしても、同一平面上にある4点でそれらを結ぶ6本の線が全て同一の色であるものが存在する。」というものである。
「グラハム問題」というのは、それでは「n がいくらより大きければ、この関係は常に成立するか。」という問題である。
グラハムの定理より、解の存在は確かとなっているが、具体的な値は現在にいたるまで得られていない。これに対して、この関係が「グラハム数」以上の n について成り立つことがグラハム自身によって証明されている。則ち、グラハム数は、この解の上限を与えていることになる。
グラハム数は、関数G(n)を
G(n)=3↑n3=3→3→n
と定義した時に
G=G64(4)=G(G(…G(4)…))(Gを64個)
を指している。
ここでG(x)の値は、以下の通りとなっている。
グラハムとブルース・リー・ロスチャイルド(Bruce Lee Rothschild)による「グラハムの定理」は、「n 次元超立方体の 2n 個の頂点のそれぞれを互いに全て線で結ぶ。次に2つの色を用いて連結した線をいずれかの色に塗り分ける。このとき n が十分大きければ、どんな塗り方をしても、同一平面上にある4点でそれらを結ぶ6本の線が全て同一の色であるものが存在する。」というものである。
「グラハム問題」というのは、それでは「n がいくらより大きければ、この関係は常に成立するか。」という問題である。
グラハムの定理より、解の存在は確かとなっているが、具体的な値は現在にいたるまで得られていない。これに対して、この関係が「グラハム数」以上の n について成り立つことがグラハム自身によって証明されている。則ち、グラハム数は、この解の上限を与えていることになる。
グラハム数は、関数G(n)を
G(n)=3↑n3=3→3→n
と定義した時に
G=G64(4)=G(G(…G(4)…))(Gを64個)
を指している。
ここでG(x)の値は、以下の通りとなっている。
という形になり、G(3)ですら、とてつもない巨大数になっている。
従って、
G(4)=3↑↑↑↑3=3↑↑↑(3↑↑↑3)=3↑↑↑G(3)
に至っては、想像もできない巨大数になっており、G=G64(4) はもう呆れてしまうしかないという数になることがわかる。
なお、その後、この解の上限について、1971年に、グラハムとロスチャイルドは、以下の「小グラハム数」という数を発表している。
F(n)= 2↑n3=2→3→n
と定義した時の
F=F7(12)=F(F(F(F(F(F(F(12)))))))
この数字は、グラハム数よりは遥かに小さいが、それでも相当に巨大な数である。
なお、グラハム問題の解の上限については、その後、さらに小さい数(それでも十分に巨大な数)が示されてきている。
一方で、グラハム問題の解の下限(この数より小さい数では成り立たない数)も研究されてきており、2008年にはジェローム・バークレー(Jerome Barkley)が 13 という数字を示している。
従って、
G(4)=3↑↑↑↑3=3↑↑↑(3↑↑↑3)=3↑↑↑G(3)
に至っては、想像もできない巨大数になっており、G=G64(4) はもう呆れてしまうしかないという数になることがわかる。
なお、その後、この解の上限について、1971年に、グラハムとロスチャイルドは、以下の「小グラハム数」という数を発表している。
F(n)= 2↑n3=2→3→n
と定義した時の
F=F7(12)=F(F(F(F(F(F(F(12)))))))
この数字は、グラハム数よりは遥かに小さいが、それでも相当に巨大な数である。
なお、グラハム問題の解の上限については、その後、さらに小さい数(それでも十分に巨大な数)が示されてきている。
一方で、グラハム問題の解の下限(この数より小さい数では成り立たない数)も研究されてきており、2008年にはジェローム・バークレー(Jerome Barkley)が 13 という数字を示している。
グラハム数を超える巨大数・表記等
ここまでで、もはや食傷気味で、いい加減にしてほしいと思われている方も多いと思うが、最後にグラハム数を超える有名な巨大数も数多く存在し、コンウェイのチェーン表記を上回るような表記法があることを述べておく。
これまで述べてきた表記法との関係では、例えば、「コンウェイのテトラトリ」と呼ばれるものは、
3→3→3→3
であるが、こんなに簡単に表記されるものが、先のグラハム数を超える巨大数になっている。
なお、巨大数を表現するための表記法等として、「拡張チェーン系の表記」、「配列表記」、「BEAF表記」、「ハイパーE表記」、「超階乗配列表記」、「(多変数)アッカーマン関数」といったものもある。
また、これらの表記法を用いても現実的かつ直接的に表現ないし近似することが不可能な「ローダー数」、「ふぃっしゅ数」(いくつかのバージョンがある)、「TREE(n)」(TREE数列)や「SCG(n)」(サブキュービックグラフ数)といった巨大数もある。
さらに、「ビジービーバー関数」1、「ラヨ数」、「巨大数庭園数」といった、有限なメモリとCPUでは計算できないほど急速に増加するため「計算不可能」とされるような関数や巨大数もある。
代表的なものでも、とても全てを列挙することはできず、またこれらの内容をここで説明することもできないので、興味・関心を抱かれた方は、さらに関連する参考図書等をご覧いただければと思っている。
1 ビジービーバー(busy beaver)とは、計算可能性理論で扱われるある種のチューリングマシンであり、この名称は「仕事人間」を意味する英語の慣用句に由来している。
これまで述べてきた表記法との関係では、例えば、「コンウェイのテトラトリ」と呼ばれるものは、
3→3→3→3
であるが、こんなに簡単に表記されるものが、先のグラハム数を超える巨大数になっている。
なお、巨大数を表現するための表記法等として、「拡張チェーン系の表記」、「配列表記」、「BEAF表記」、「ハイパーE表記」、「超階乗配列表記」、「(多変数)アッカーマン関数」といったものもある。
また、これらの表記法を用いても現実的かつ直接的に表現ないし近似することが不可能な「ローダー数」、「ふぃっしゅ数」(いくつかのバージョンがある)、「TREE(n)」(TREE数列)や「SCG(n)」(サブキュービックグラフ数)といった巨大数もある。
さらに、「ビジービーバー関数」1、「ラヨ数」、「巨大数庭園数」といった、有限なメモリとCPUでは計算できないほど急速に増加するため「計算不可能」とされるような関数や巨大数もある。
代表的なものでも、とても全てを列挙することはできず、またこれらの内容をここで説明することもできないので、興味・関心を抱かれた方は、さらに関連する参考図書等をご覧いただければと思っている。
1 ビジービーバー(busy beaver)とは、計算可能性理論で扱われるある種のチューリングマシンであり、この名称は「仕事人間」を意味する英語の慣用句に由来している。
最後に
今回は、数詞では表現されないさらなる巨大数を表現するために、四則演算やべき乗等の演算を一般化した「ハイパー演算」の概念や各種の表記法等について紹介してきた。既に述べたように、ここで紹介したものは、巨大数に関するテーマの一部でしかない。いろいろな名称が付与された巨大数が多数存在している。あるいは必ずしも巨大数ということがメインのテーマではないものの、結果的に巨大数の形成に関わってくるような関数やそれらのベースになる各種の理論や体系等についての研究も行われてきている。その意味で、前回の研究員の眼の冒頭で述べたように、「巨大数」の世界は奥が深くで、どこまで行っても切りがないところがある。
と、ここまで、いろいろな巨大数の一端を紹介してきたが、結局はいかなる巨大数といえども、言ってしまえば、有限数であることに変わりはなく、無限とは一線を画したものとなっている。まさに、この「有限」と「無限」の狭間の中で、過去から巨大数が関係するような研究等も行われてきていると言えるのかもしれない。
学問的には各種の理論や概念等が生まれ、その派生的な結果等として、我々が想像もできない巨大数や巨大関数が生まれてくることになるのかもしれない。ただし、少なくとも実世界を見渡した時には、地球上で観測されるものは、これまでの科学の分析によれば、如何に無限のように見えても、何らかの形で有限に集約されているといえることになる。そして、それらは前回の研究員の眼で紹介したように、(今回の研究員の眼を踏まえて振り返ってみれば)一定程度我々が認識できる(?)レベルでの巨大数で表現されている。
地球は有限の世界の存在であるが、果てしない(と言われる)宇宙が有限なのか無限なのかについては、いろいろな考え方があるようだ。観測可能な宇宙の広さ(大きさ)についても、宇宙が約138億年前に誕生したとすれば、少なくとも約138億光年(1光年は約9兆4,600億km)(≒1.3×1023km)はある(ここまで、この研究員の眼をお読みいただいた方にとっては、逆に何だ、その程度の桁数なのかとの印象を持たれてしまうかもしれない)ようだが、これについても実際はさらに大きく、さらには現在でも拡大しているとも言われているようだ。
いずれにしても、現代の科学技術をもってしても、宇宙の解明は未だ途上にあり、その中にあっても、現時点において観測可能な宇宙は宇宙全体のほんの一部に過ぎない、と言うことなのだろう。
その意味で、果てしなく「巨大数」の世界を探求することに、何となくロマンを感じる人がいるのも十分に理解できるのではないかと思われる。
と、ここまで、いろいろな巨大数の一端を紹介してきたが、結局はいかなる巨大数といえども、言ってしまえば、有限数であることに変わりはなく、無限とは一線を画したものとなっている。まさに、この「有限」と「無限」の狭間の中で、過去から巨大数が関係するような研究等も行われてきていると言えるのかもしれない。
学問的には各種の理論や概念等が生まれ、その派生的な結果等として、我々が想像もできない巨大数や巨大関数が生まれてくることになるのかもしれない。ただし、少なくとも実世界を見渡した時には、地球上で観測されるものは、これまでの科学の分析によれば、如何に無限のように見えても、何らかの形で有限に集約されているといえることになる。そして、それらは前回の研究員の眼で紹介したように、(今回の研究員の眼を踏まえて振り返ってみれば)一定程度我々が認識できる(?)レベルでの巨大数で表現されている。
地球は有限の世界の存在であるが、果てしない(と言われる)宇宙が有限なのか無限なのかについては、いろいろな考え方があるようだ。観測可能な宇宙の広さ(大きさ)についても、宇宙が約138億年前に誕生したとすれば、少なくとも約138億光年(1光年は約9兆4,600億km)(≒1.3×1023km)はある(ここまで、この研究員の眼をお読みいただいた方にとっては、逆に何だ、その程度の桁数なのかとの印象を持たれてしまうかもしれない)ようだが、これについても実際はさらに大きく、さらには現在でも拡大しているとも言われているようだ。
いずれにしても、現代の科学技術をもってしても、宇宙の解明は未だ途上にあり、その中にあっても、現時点において観測可能な宇宙は宇宙全体のほんの一部に過ぎない、と言うことなのだろう。
その意味で、果てしなく「巨大数」の世界を探求することに、何となくロマンを感じる人がいるのも十分に理解できるのではないかと思われる。
(2022年02月16日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月17日
EUの金融システムのリスクと脆弱性(2025秋)-欧州の3つの金融監督当局の合同委員会報告書 -
2025年10月17日
日本における「老衰死」増加の背景 -
2025年10月17日
選択と責任──消費社会の二重構造(1)-欲望について考える(2) -
2025年10月17日
首都圏の中古マンション価格~隣接する行政区単位での価格差は?~ -
2025年10月17日
「SDGs疲れ」のその先へ-2015年9月国連採択から10年、2030年に向け問われる「実装力」
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【巨大数について(その2)-ハイパー演算、各種の表記法等-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
巨大数について(その2)-ハイパー演算、各種の表記法等-のレポート Topへ


















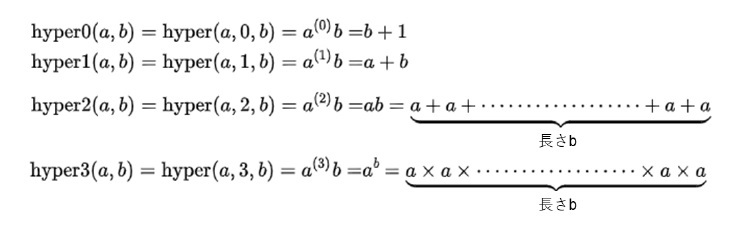
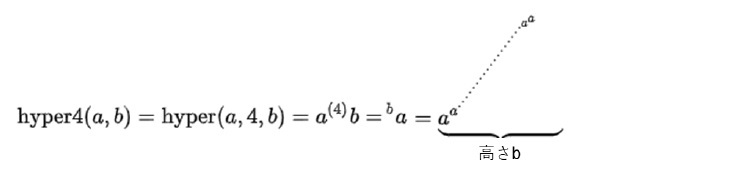
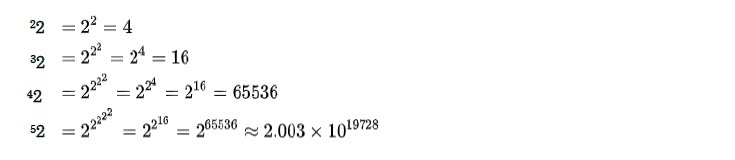
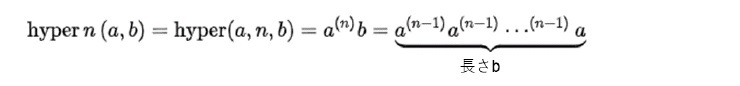

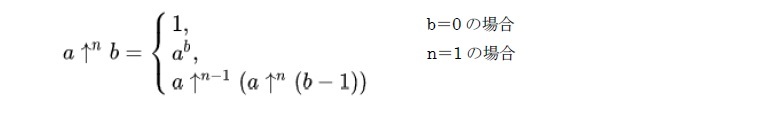

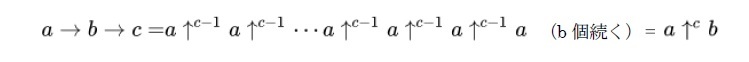
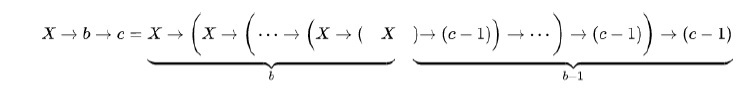
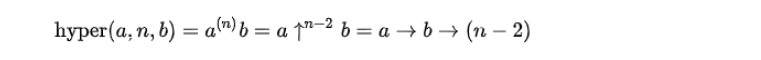


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




