- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 巨大数について(その1)-数詞で表現される巨大数等-
コラム
2022年02月09日
文字サイズ
- 小
- 中
- 大
はじめに
今回は「巨大数」1について何回かに分けて説明していきたいと思っている。
「巨大数」というのは、まさにその言葉通りで、我々が日常生活で使用している数よりもはるかに大きな数、のことを指している。非常に巨大な数については「天文学的数字」と呼ばれることもある。ただし、その厳密な定義があるわけではない。巨大数についての研究は「巨大数論」とか、後に説明する「グーゴㇽ(googol)」に因んで「グーゴロジー(googology)」と呼ばれている。
その世界はある意味で奥が深くて、いまだ日々進化しており、どこまで説明しても切りがないところがあるように思われる。今回は、ある程度のところまで、またそれぞれの項目についての紹介も簡単に留めることにしたい。
まずは今回の研究員の眼では、数詞で表現される巨大数(あるいは巨大な数を表す数詞)を中心に、我々が通常、感覚的に認識可能で、指数関数で表現できるような巨大数について紹介したい。
1 巨大数に対する英語は「huge numbers」だと多くの人は思われるかもしれないが、英語のサイト等ではむしろ「大きな数」を意味している「large numbers」が使用されている。
「巨大数」というのは、まさにその言葉通りで、我々が日常生活で使用している数よりもはるかに大きな数、のことを指している。非常に巨大な数については「天文学的数字」と呼ばれることもある。ただし、その厳密な定義があるわけではない。巨大数についての研究は「巨大数論」とか、後に説明する「グーゴㇽ(googol)」に因んで「グーゴロジー(googology)」と呼ばれている。
その世界はある意味で奥が深くて、いまだ日々進化しており、どこまで説明しても切りがないところがあるように思われる。今回は、ある程度のところまで、またそれぞれの項目についての紹介も簡単に留めることにしたい。
まずは今回の研究員の眼では、数詞で表現される巨大数(あるいは巨大な数を表す数詞)を中心に、我々が通常、感覚的に認識可能で、指数関数で表現できるような巨大数について紹介したい。
1 巨大数に対する英語は「huge numbers」だと多くの人は思われるかもしれないが、英語のサイト等ではむしろ「大きな数」を意味している「large numbers」が使用されている。
無量大数
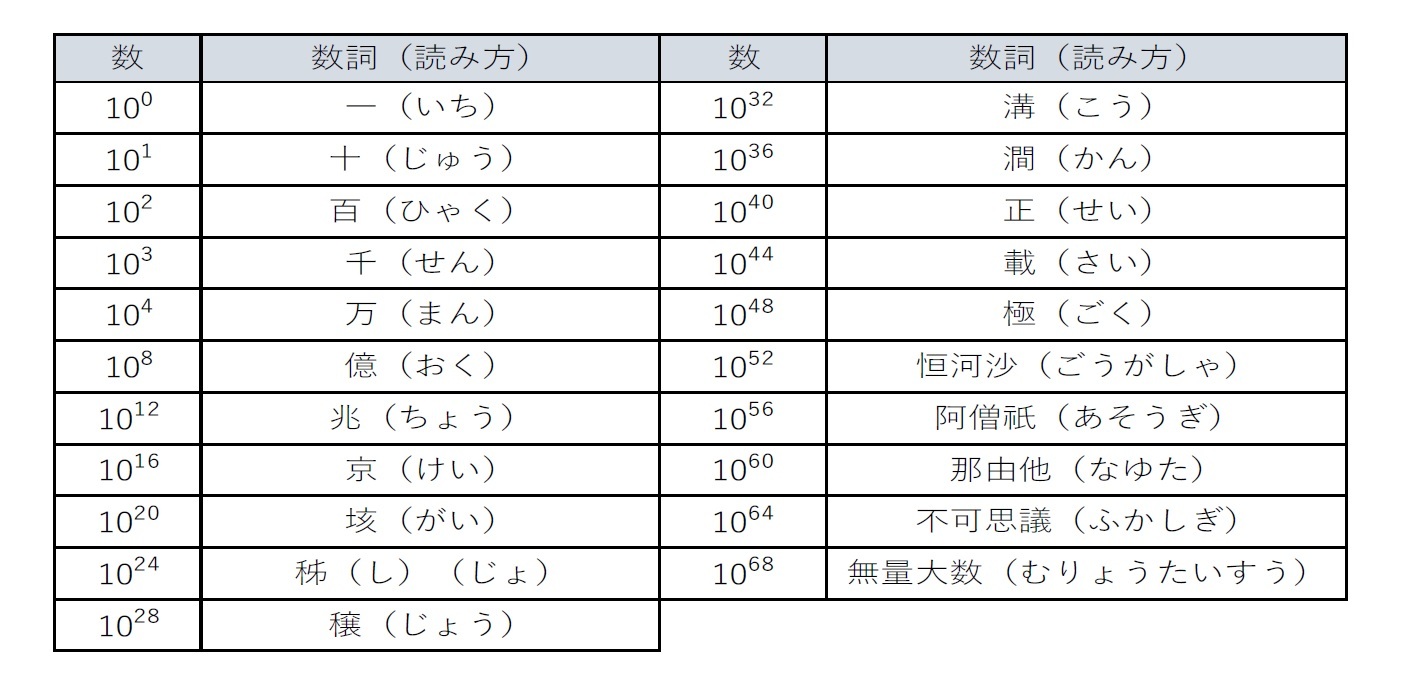
「無量大数(むりょうたいすう)」という言葉はご存じの方も多いと思われる。無量大数は、漢字文化圏において名前が付与されている最大数を表している。無量大数がいくつを示すかは、時代や地域によっても異なっており、現在でも人によっては解釈が分かれるようであるが、一般的には「1068」を指しているとされている。そして、この場合の無量大数までの数詞は、次ページの図表の通りとなっている。
これらの数詞は中国から来ているが、恒河沙、阿僧祇、那由他、不可思議は仏教に由来しており、「無量大数」も元々は仏教用語の「無量数」(量ることができないほど大きな数)から来ている。「恒河沙」はガンジス川にある無数の砂2を意味しており、「阿僧祇」は「数えることができない」という意味を有し、仏典では、成仏するまでに必要な時間の長さを表すのに使用されている。「那由他」は、「極めて大きな数量」を意味しており、「不可思議」は、仏の智慧や神通力は思いはかったり言葉で言い表したりすることはできないことから、これが転じて、それほど大きい数字を表す、とされている。
この図表が示しているように、「万」までは1桁ごとに新たな数詞が付与されているが、「万」以降は、4桁ごとに新たな数詞が付与されるものとなっており、これを「万進法」と呼んでいる3を。
なお、「無量大数」は、銀河系に含まれる原子の総数に概ね相当していると言われている。
因みに、宇宙の年齢は138億年と推定されているようだが、これを秒数で表すと1年が31,536,000秒(=365日×24時間×60分×60秒)となることから、宇宙の年齢は、4.351968×1017秒となる。則ち、「無量大数」は言うに及ばず、「垓(=1020)」ですら、宇宙誕生以来、数を毎秒1回のペースで数えたとしても、未だたどり着けていない、ということになる。
これらの数詞は中国から来ているが、恒河沙、阿僧祇、那由他、不可思議は仏教に由来しており、「無量大数」も元々は仏教用語の「無量数」(量ることができないほど大きな数)から来ている。「恒河沙」はガンジス川にある無数の砂2を意味しており、「阿僧祇」は「数えることができない」という意味を有し、仏典では、成仏するまでに必要な時間の長さを表すのに使用されている。「那由他」は、「極めて大きな数量」を意味しており、「不可思議」は、仏の智慧や神通力は思いはかったり言葉で言い表したりすることはできないことから、これが転じて、それほど大きい数字を表す、とされている。
この図表が示しているように、「万」までは1桁ごとに新たな数詞が付与されているが、「万」以降は、4桁ごとに新たな数詞が付与されるものとなっており、これを「万進法」と呼んでいる3を。
なお、「無量大数」は、銀河系に含まれる原子の総数に概ね相当していると言われている。
因みに、宇宙の年齢は138億年と推定されているようだが、これを秒数で表すと1年が31,536,000秒(=365日×24時間×60分×60秒)となることから、宇宙の年齢は、4.351968×1017秒となる。則ち、「無量大数」は言うに及ばず、「垓(=1020)」ですら、宇宙誕生以来、数を毎秒1回のペースで数えたとしても、未だたどり着けていない、ということになる。
2 実際のガンジス川の砂粒は1022程度と見積もられているようである。
3 一方で、アラビア数字を使用して数値を表す場合には、三桁ごとにコンマや空白を設ける等の表記がなされ、英語等の西洋方式に準じたものとなっている。これらの状況については別途の研究員の眼で報告することとする。
不可説不可説転
一般的には「無量大数」が最大の数詞と考えられているが、例えば、仏教経典の「華厳経(八十華厳)」にはさらに大きな数も表す123の命数(数詞)が記述されており、n番目の命数は10の
7×2(n-1)乗になっている。
これによれば、以下の図表が示すように「倶胝(くてい)」(=10⁷)をスタートに、倶胝の倶胝倍(倶胝の二乗)(=1014)が「阿庾多(あゆた)」、阿庾多の阿庾多倍が「那由他(なゆた)」(=1028)という形で、べき乗の係数が倍々で増えていく形になっている。即ち、それまでの数詞を全て使用しても表現できない数を新たな数詞で表現する形になっている。
この最後の123番目の数詞が「不可説不可説転(ふかせつふかせつてん)」と呼ばれるもので、
7×2(n-1)乗になっている。
これによれば、以下の図表が示すように「倶胝(くてい)」(=10⁷)をスタートに、倶胝の倶胝倍(倶胝の二乗)(=1014)が「阿庾多(あゆた)」、阿庾多の阿庾多倍が「那由他(なゆた)」(=1028)という形で、べき乗の係数が倍々で増えていく形になっている。即ち、それまでの数詞を全て使用しても表現できない数を新たな数詞で表現する形になっている。
この最後の123番目の数詞が「不可説不可説転(ふかせつふかせつてん)」と呼ばれるもので、
となっている。
「不可説」というのは、「悟りの境地は言葉では説明できない」ということを意味している。なお、これに至るまでの名称は、112番「不可数」(数えることができない)、114番「不可称」(称えることができない)、116番「不可思」(思うこともできない)、118番「不可量」(量ることができない)、120番が「不可説」となっており、それぞれの文字が表す意味合いの重さのレベルが反映される形になっている。また、これらの数詞の後に「転」という漢字を最後に付与した数詞が使用されているが、これはべき乗を倍にすることを意味しているようだ。
いずれにしても、「不可説不可説転」は、無量大数とは比較にならないほど大きな数(無量大数の5400溝(1032)乗がおよそ1不可説不可説転)を表しており、後に紹介するように、これに相当するものを現実の世界で示すことは難しい。
従って、これらの数は、あくまでも実用的な数ではなく、計算できないほどの大きな数を示すことで、人間には想像もできず、また到達が困難な、悟りの功徳の大きさを表している、とされているようだ。
「不可説」というのは、「悟りの境地は言葉では説明できない」ということを意味している。なお、これに至るまでの名称は、112番「不可数」(数えることができない)、114番「不可称」(称えることができない)、116番「不可思」(思うこともできない)、118番「不可量」(量ることができない)、120番が「不可説」となっており、それぞれの文字が表す意味合いの重さのレベルが反映される形になっている。また、これらの数詞の後に「転」という漢字を最後に付与した数詞が使用されているが、これはべき乗を倍にすることを意味しているようだ。
いずれにしても、「不可説不可説転」は、無量大数とは比較にならないほど大きな数(無量大数の5400溝(1032)乗がおよそ1不可説不可説転)を表しており、後に紹介するように、これに相当するものを現実の世界で示すことは難しい。
従って、これらの数は、あくまでも実用的な数ではなく、計算できないほどの大きな数を示すことで、人間には想像もできず、また到達が困難な、悟りの功徳の大きさを表している、とされているようだ。
英語の場合の巨大数の数詞
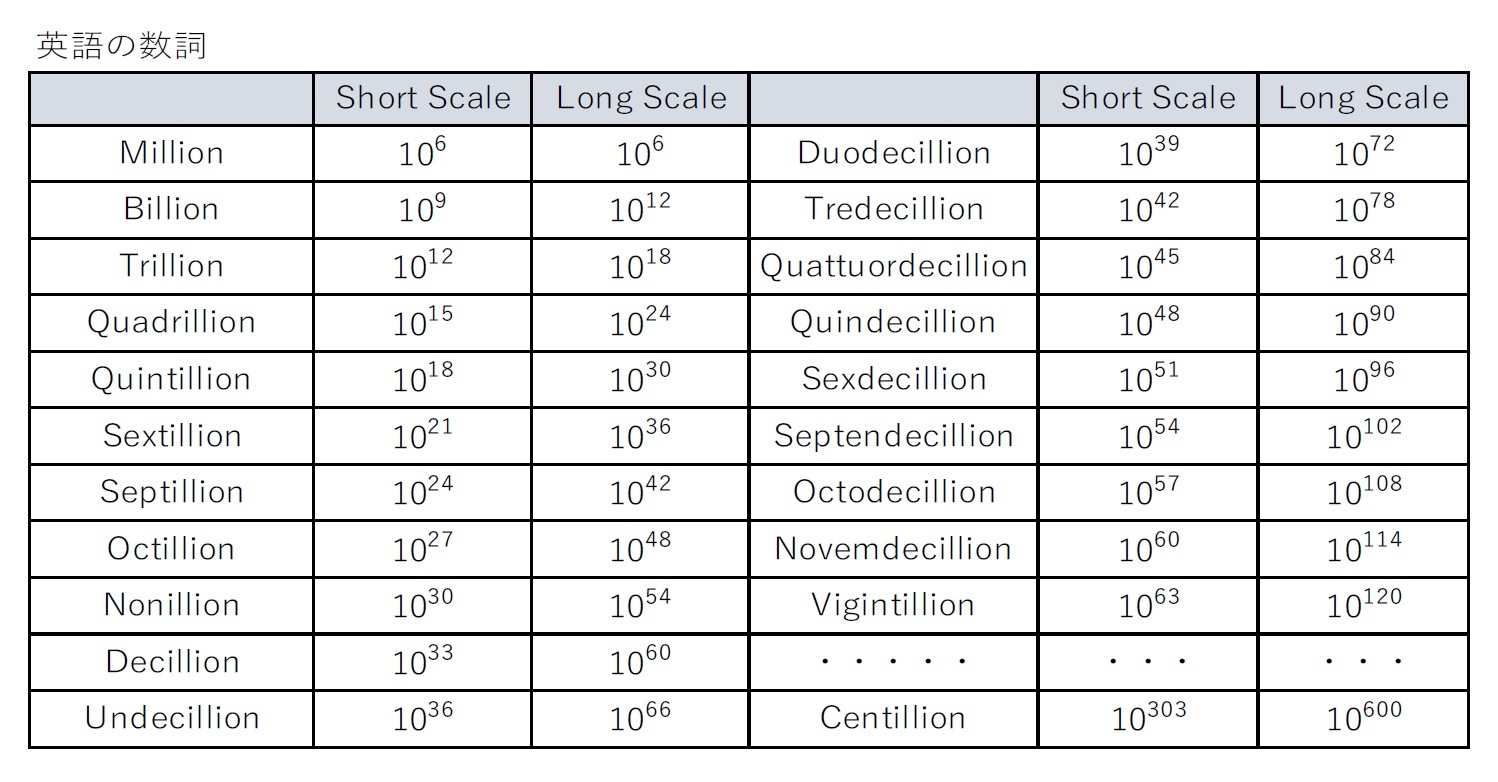
英語の命数法には、「short scale」と「long scale」と呼ばれる2種類があり、それぞれ以下の図表の通りとなっている。short scaleでは、1,000倍ごとに新しい名前が付与され、long scaleでは、1,000,000倍ごとに新しい名前が付与される。
なお、英国やオーストラリア、ニュージーランド等では、以前はlong scaleが使用されていたが、最近は大部分がshort scaleに移行している。結果として、現在ではほぼ米国や英国等の英語圏ではshort scaleが、英語圏以外の大陸欧州(中・西欧)ではlong scaleが使用されているようである。
また、これによれば、最も大きな数詞は、「centillion」(=10303)となっている。即ち、「million」からスタートして、3ないしは6ずつべき乗が増加していき、100番目に相当するものが、数字の100を表す接頭辞である「centi」を使用した「centillion」となっている。
なお、図表にはないが、「vigintillion」の「viginti」は20(番目の)を意味しており、その次は21を意味する「unviginti」を使用した「unvigintillion(Short Scaleでは1066)」等と続いていくことになる。これにより、無量大数(1068)は、英語(Short Scale)ではone hundred unvigintillionと表現されることになる。
なお、英国やオーストラリア、ニュージーランド等では、以前はlong scaleが使用されていたが、最近は大部分がshort scaleに移行している。結果として、現在ではほぼ米国や英国等の英語圏ではshort scaleが、英語圏以外の大陸欧州(中・西欧)ではlong scaleが使用されているようである。
また、これによれば、最も大きな数詞は、「centillion」(=10303)となっている。即ち、「million」からスタートして、3ないしは6ずつべき乗が増加していき、100番目に相当するものが、数字の100を表す接頭辞である「centi」を使用した「centillion」となっている。
なお、図表にはないが、「vigintillion」の「viginti」は20(番目の)を意味しており、その次は21を意味する「unviginti」を使用した「unvigintillion(Short Scaleでは1066)」等と続いていくことになる。これにより、無量大数(1068)は、英語(Short Scale)ではone hundred unvigintillionと表現されることになる。
googol(グーゴル)、googolplex(グーゴルプレックス)
1googolは、下記で紹介するように、観測可能な宇宙に存在する素粒子の数よりも大きいが、チェスや将棋や囲碁のゲーム木4(手法)の数よりは小さい、と言われている。一方で、1googolplexはとてつもなく巨大な数で、そもそも、観測可能な宇宙の質量を全て利用しても1 googolplexを十進法で印刷することはできない、と言われている。
4 組合せゲーム理論において、ゲームの盤面を有向グラフのノード(点、節)で、手をエッジ(線、枝)で表したもの
4 組合せゲーム理論において、ゲームの盤面を有向グラフのノード(点、節)で、手をエッジ(線、枝)で表したもの
これまで紹介した数字の比較
なお、ここまで紹介してきた数詞単位を比較すると、以下の通りとなっている。
無量大数 <googol < Centillion < 不可説不可説転 < googolplex
仏教の世界で考えられていた最大の数詞である「不可説不可説転」も、「googolplex(グーゴルプレックス)」と比較すれば、(1063の桁数レベルの違いがある)極めて小さな数ということになる。
無量大数 <googol < Centillion < 不可説不可説転 < googolplex
仏教の世界で考えられていた最大の数詞である「不可説不可説転」も、「googolplex(グーゴルプレックス)」と比較すれば、(1063の桁数レベルの違いがある)極めて小さな数ということになる。
(参考)キロ,メガ,ギガ
身近(?)な巨大数
それでは、実際に身近(?)に見られる巨大数としては、どのようなものがあるのだろうか。
これについては、例えば以下のようなものが挙げられる(一部の数値については、各種の推定値がある中で、1つの例示数値を挙げているので、ここでの数値には異論があるかもしれない。あくまでも巨大数のレベル感を知るためのものとして、参考程度に留めていただきたい)。
1.金融・経済関係
・日本のGDP(2020年) 約500~550兆円(=5.0~5.5×1014円)
・世界のGDP(2020年) 約9千兆円(=9×1015円)
2.物理学・天文学関係
・地球の質量 約5.9724×1024kg
・太陽の質量 約1.989×1030kg (地球の約33.3万倍)
・アボガドロ定数(物質量 1 mol を構成する粒子の個数を示す定数)(高校の化学で出てくる)
6.02214076×1023 mol−1
・地球上に存在する原子の数 100極個(1050個)レベル
・エディントン数(観測可能な宇宙に存在する陽子の数としてアーサー・エディントンが予想した数)
136 × 2256 ≒ 1.575 × 1079
・観測可能な宇宙に存在する素粒子の数 1097個レベル
なお、「宇宙論で登場した最大の数」として、以下が挙げられている。
・宇宙のポアンカレ回帰時間(複数の宇宙の全質量を1個のブラックホールに圧縮して、その蒸発後に、ポアンカレの回帰定理に従い、再びブラックホールができるまで時間)
これについては、例えば以下のようなものが挙げられる(一部の数値については、各種の推定値がある中で、1つの例示数値を挙げているので、ここでの数値には異論があるかもしれない。あくまでも巨大数のレベル感を知るためのものとして、参考程度に留めていただきたい)。
1.金融・経済関係
・日本のGDP(2020年) 約500~550兆円(=5.0~5.5×1014円)
・世界のGDP(2020年) 約9千兆円(=9×1015円)
2.物理学・天文学関係
・地球の質量 約5.9724×1024kg
・太陽の質量 約1.989×1030kg (地球の約33.3万倍)
・アボガドロ定数(物質量 1 mol を構成する粒子の個数を示す定数)(高校の化学で出てくる)
6.02214076×1023 mol−1
・地球上に存在する原子の数 100極個(1050個)レベル
・エディントン数(観測可能な宇宙に存在する陽子の数としてアーサー・エディントンが予想した数)
136 × 2256 ≒ 1.575 × 1079
・観測可能な宇宙に存在する素粒子の数 1097個レベル
なお、「宇宙論で登場した最大の数」として、以下が挙げられている。
・宇宙のポアンカレ回帰時間(複数の宇宙の全質量を1個のブラックホールに圧縮して、その蒸発後に、ポアンカレの回帰定理に従い、再びブラックホールができるまで時間)
3.生体関係
・人間の体の細胞数 約60兆個(=6×1013個)
・人間のシナプス(神経細胞の接続)数 約150兆本(=1.5×1014本)
4.組み合わせ
・3×3のルービックキューブの組み合わせ数 約4325京通り(=4.325×1018通り)
・トランプ52枚の組み合わせ数(52!) 約8066不可思議通り(=8.066×1067通り)
(つまり、無量大数の8割程度)
以下のゲームの推定値は、各種の前提に基づくものであり、完全解析は困難とされているようだ。
・シャノン数(チェスのゲーム木(手法)のサイズ) 10120 通り
(一方で、実現可能な局面数としては 1043 通り)
・将棋のゲーム木(手法)のサイズ 10220 通り(実現可能な局面数としては 1062~70 通り)
・囲碁の実現可能な局面数 2.081681994×10170 通り
5.数学関係
・巨大な素数(2018年12月時点で確認されている最大素数)
282,589,933 – 1 (≈ 1.488×1024862047)(24,862,048 桁)
・なお、素数分布に関する「スキューズ数」と呼ばれるものもあり、以下の通りである。
・人間の体の細胞数 約60兆個(=6×1013個)
・人間のシナプス(神経細胞の接続)数 約150兆本(=1.5×1014本)
4.組み合わせ
・3×3のルービックキューブの組み合わせ数 約4325京通り(=4.325×1018通り)
・トランプ52枚の組み合わせ数(52!) 約8066不可思議通り(=8.066×1067通り)
(つまり、無量大数の8割程度)
以下のゲームの推定値は、各種の前提に基づくものであり、完全解析は困難とされているようだ。
・シャノン数(チェスのゲーム木(手法)のサイズ) 10120 通り
(一方で、実現可能な局面数としては 1043 通り)
・将棋のゲーム木(手法)のサイズ 10220 通り(実現可能な局面数としては 1062~70 通り)
・囲碁の実現可能な局面数 2.081681994×10170 通り
5.数学関係
・巨大な素数(2018年12月時点で確認されている最大素数)
282,589,933 – 1 (≈ 1.488×1024862047)(24,862,048 桁)
・なお、素数分布に関する「スキューズ数」と呼ばれるものもあり、以下の通りである。
これ以外にも「グラハム数」等の有名な巨大数があるが、これらについては次回の研究員の眼で紹介することにする。
最後に
今回は、巨大数の中で、数詞で表現される巨大数(あるいは巨大な数を表す数詞)を中心に紹介してきた。数詞で表現されているとは言え、通常は馴染みのない巨大な数字の世界なので、そんなものか程度に思われたかもしれない。それでも、我々がある程度理解でき、観測可能な数字の世界の中でも、このような巨大数の世界があるのだということを、少しでも認識していただければと思っている。
今回の研究員の眼で紹介した巨大数は、何とか階段状の指数表記で表現できるようなものとなっているが、これは巨大数全体のスケール感から言えば、まだまだと言えるものである。次回の研究員の眼では、数詞や指数表記等では表現が難しい、さらなる巨大数を表現するために、四則演算やべき乗等の演算を一般化した「ハイパー演算」の概念等があるので、これらについて紹介する。
今回の研究員の眼で紹介した巨大数は、何とか階段状の指数表記で表現できるようなものとなっているが、これは巨大数全体のスケール感から言えば、まだまだと言えるものである。次回の研究員の眼では、数詞や指数表記等では表現が難しい、さらなる巨大数を表現するために、四則演算やべき乗等の演算を一般化した「ハイパー演算」の概念等があるので、これらについて紹介する。
(2022年02月09日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/13 | 数字の「27」に関わる各種の話題-27は3の3乗だが- | 中村 亮一 | 研究員の眼 |
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月21日
貿易統計25年10月-米国向け自動車輸出が持ち直し -
2025年11月21日
消費者物価(全国25年10月)-コアCPI上昇率は25年度末にかけて2%を割り込む公算 -
2025年11月20日
持続可能なESGを求めて-目標と手段とを取り違えないこと -
2025年11月20日
「ラブブ」とは何だったのか-SNS発の流行から考える“リキッド消費” -
2025年11月19日
1ドル155円を突破、ぶり返す円安の行方~マーケット・カルテ12月号
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【巨大数について(その1)-数詞で表現される巨大数等-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
巨大数について(その1)-数詞で表現される巨大数等-のレポート Topへ


















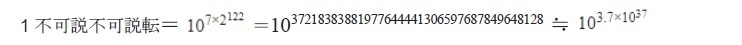




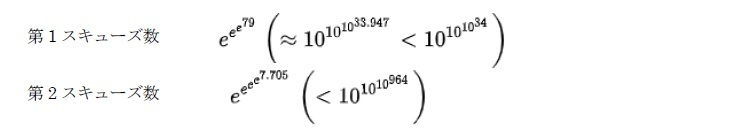

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




