コラム
2021年06月04日

「対数」に、もう一度興味・関心を持ってみませんか（その１）－対数って、何だろう？－

このレポートの関連カテゴリ

Xでシェアする Facebookでシェアする

文字サイズ

  • 小
  • 中
  • 大
全文ダウンロード（PDF）

はじめに

以前の研究員の眼で、3回のシリーズで「ネイピア数e」に関する話題について紹介した。そこで、ネイピア数eは「自然対数の底」だと述べたが、自然対数を表現する場合には底のeは省略されることになる。一方で、指数関数の表現ではeは常に明示されるので、eについては対数というよりもむしろ指数としての印象が強いと思われる。ところが、ネイピア数のネイピアは、対数の発見者であるとも言われており、対数が指数よりも先に広く認知されてきた。

また、多くの人の感覚としては、「指数関数的に増加する」という表現によく触れる機会があることからわかるように、指数（関数）については一定の馴染みがあると思われる。ところが、対数（関数）と言われると、「それは何だ」というような感じで、アレルギー反応を起こして、ちょっと身構えてしまう方が多いのではないかと思われる。

対数関数は、指数関数の逆関数1である。一般的に、逆関数の関係にある２つの関数の一方は理解しやすいが他方は理解しがたいというケースが多くみられるものと思われる。

今後の複数回の研究員の眼で、「対数」に関する話題について、その意味合い及び有用性を含めて紹介していくこととしたい。まずは、今回は「対数」の概念等について説明する。
 
1 一般的にある関数（y=f(x)）が与えられた時に、そのxとyを入れ替えて、yについて解いた関数（x=f-1(y)）を、元の関数の「逆関数」という。

対数とは

「対数（logarithm）」というのは、ある数  aをp乗してbになるとした場合、即ちb= ap となる場合の、べき指数p のことを指しており、このp を「 aを底（てい）とする b の対数」と呼ぶ。このpが loga bと表現され、aは「底（てい）（base）」、b は「真数（antilogarithm）」と呼ばれる（なお、通常、a≠0、a>0、b>0として、実数の対数が定義される）。

則ち、以下の関係となる。
対数
また、一般的な変数 x に対応する対数を与える関数を「対数関数」と呼び、通常 loga x と表されるが、これによれば以下の関係となる。
対数関数

なぜ対数と呼ばれるのか（対数の語源）

対数のイメージが良くないことの理由の１つに、恐らく急に出てくる「log」という記号や聞きなれない「対数」や「底」という用語があるように思われる。そこで、まずはこれらの記号や用語の由来について説明する。

「log」という記号は、対数の英語の「logarithm（ロガリズム）」の略語になっている。この英語は、ラテン語の「Logarithmorum 」に由来しており、これはギリシャ語の、「言葉（word）」、「論理」、さらには「比率（proportionあるいはratio）」を意味する「logos（ロゴス）」と、「数字（number）」を意味する「arithmos（アリトモス）」が語源となっている。

それでは、日本語ではなぜ「対数」と言うのだろうか。これについては、「17世紀の中国で、西欧の対数が紹介された時、x とlog x を対にしてならべた表を『対数表（table of corresponding numbers）』と述べた」ことに由来しているようである（このように、数学用語の日本語は、まずは西洋数学が中国で紹介されたときの中国語への翻訳に由来しているものが多い）。

「底」という用語は、まさに英語の「base」を翻訳したもので、「基底」や「基数」といった意味になるのだろうが、「底」では今ひとつピンとこないと感じるのは個人的にはよく理解できる気もする。

ネイピア等による対数概念の構築

さて、それではこのような名称を付与したのは誰かということになる。これについては、以前の研究員の眼で紹介した「ネイピア数e」のジョン・ネイピア（John Napier：1550～1617）であると言われている。スコットランドのバロンであったネイピアは、三角関数等の厖大な計算を単純化する手段として、1594年に「対数」の概念を提唱し、1614年に発表した論文「Mirifici Logarithmorum Canonis Descriptio（驚くべき対数表の使い方）」で、いわゆる「対数表」を示した。

当時はケプラーやガリレオといった偉大な天文学者が活躍していた時代で、惑星の軌道や望遠鏡による星の観測等の天文学の研究が盛んに行われていた時代であった。さらには、大航海時代で、船乗りたちが星の位置に基づいて、船の現在の位置を確認する必要があり、精密な天体観測が要求されていた。

そうした中で、天文学者は巨大な数を扱う計算に苦労していたが、コンピューター等が無い時代において、複雑な計算を簡略化するために、対数の概念が考案された。あらかじめ、いろいろな対数の値を算出して一覧表にまとめた「対数表」を作成しておくことで、下記に説明する「対数に関する基本公式」に見られる対数の特性を利用して、巨大な数の計算の効率化が図られることになった。

ネイピアについては、彼自身が現在良く知られているようなネイピア数eを示していたわけではなかったが、最も古くに研究を行ったことから、その名前が付されている、と紹介した。同様に、ネイピアは「対数発見者」であると言われる2が、ネイピアが提唱した対数の定義も現在用いられているものとは異なっていた。

ネイピアによれば、正の実数 x に対して

ｘ＝107（1－1／107）y

を満たす実数としてただ1つ定まるy のことを「ネイピアの対数（Napierian logarithm）」と呼んでいた。

上式を変形すると

ｘ／107＝｛（1－1／107）10⁷ ｝y／10⁷

となる。これは、（1－1／107）10⁷　が（現行定義における）この対数の底であることを意味している。

計算してみればわかるが、

（1－1／107）10⁷＝0.3678942…　≒1／e  （eはネイピア数）

となっていることが確認できる。

これに対して、イングランドの数学者であるヘンリー・ブリッグス（Henry Briggs）は、ネイピアとネイピアの対数表の改良を検討した結果、1624年に、底を10とする「常用対数」を計算した対数表「Arithmetica Logarithmica（対数算術）」を出版した。この対数表は、1～20,000及び90,001～100,000という3万個の自然数をカバーしていた。その後、1628年にオランダのアドリアン・フラック（Adriaan Vlacq）によって、1～100,000までの残りの数がカバーされた。

18世紀から19世紀にかけての著名なフランスの数学者、物理学者、天文学者であるピエール＝シモン・ラプラス（Pierre-Simon Laplace）は、「対数は天文学者の寿命を2倍に延ばした」と述べたと言われている。
 
2 スイスの時計職人、天文機器製作者であったヨスト・ビュルギ（Jost Bürgi）が、ネイピアよりも早く1588年に対数の概念を発見したが、1620年まで公表しなかったため、対数の発見者としてはネイピアの名前が挙げられることが多い。

自然対数と常用対数

対数において、ネイピア数e（=2.718281…）を底とするものを「自然対数（natural logarithm）」と呼び、一般的な記法に基づく「loge x」 だけでなく、「ln x」や（底を記載せずに）「log x」等で表現される。

これに対して、10を底とするものを「常用対数（common logarithm）」と呼び、記号「log10 x」で表現される。

先に述べた対数表作成者の名前を冠して、自然対数は「ネイピアの対数」、常用対数は「ブリッグスの対数」とも呼ばれる。

常用対数の値は、その真数の十進法表示での桁数の目安になり、x が自然数のとき、x の桁数は、log x の整数部分 ⌊log x⌋ に 1 を足した数に等しくなる。また、0 < x < 1 のとき、x の小数首位（小数点以下に最初に現れる0 でない桁）は、−⌊log x⌋ となる。

常用対数は、「常用」との名称が付されているように、音の大きさ（デシベル）、地震のマグニチュード、水素イオン指数（pH）といった各種の科学的な測定値を表現する際に用いられて、実際に使用されているケースが多い。

一方で、自然対数は、数学等の理論分野で使用されている。学生時代に学んだ時や試験問題等では、こちらの自然対数の方が多く現れてきたことを覚えておられるのではないかと思われる。

一般的な感覚としては、十進法に慣れ親しんでいることから、底を10とする常用対数の方が「自然」に感じられるかもしれない。ところが、数学的にはeを底とする自然対数の方が、例えば単純な積分やテイラー級数で極めて容易に定義でき、微積分等の計算が簡便になること等の理由で、より扱いやすく「自然」と認識されることになる。

自然対数と常用対数の関係は、（後に述べる）底の変換公式を用いることにより、自然対数の値を log10 e ≒ 0.43 倍すれば、常用対数の値になる。逆に常用対数の値をloge10 ≒ 2.303 倍すれば、自然対数の値になる。

なお、これ以外にも、底を2とする「二進対数（binary logarithm）」は、情報理論の分野で情報量等を表現する場合や音楽の分野等で用いられており、「lb」という記号が使用されたりする。

対数に関する基本公式等

ここでは、対数に関する基本公式等を示しておく。これを説明するのがこの研究員の眼の主旨ではないので、ここでは証明等は示していない。

ただし、重要なことは、この基本公式等からわかるように、対数を用いると、「掛け算が足し算に、割り算が引き算に、n乗がn倍に、n乗根が１／n倍に」なることから、特に大きな数を扱う場合の計算が楽になることになる。
対数に関する基本公式等
ここで、この公式を利用した具体的な使用例を示しておく。
 

4桁の数字の掛け算「3275×8194」を考える。これをそのまま計算するのは、電卓であれば一瞬であるが、手計算で行うのは容易ではない。ところが10以下の数値に関する小数点以下6桁を有する常用対数表を用いると、以下の通りとなる。　

log10 3275＝log10 (3.275×1000）＝log10 3.275＋log10 1000　　
　　　　　＝0.515211＋3＝3.515211

log10 8194＝log10 (8.194×1000）＝log10 8.194＋log10 1000　　
　　　　　＝0.913496＋3＝3.913496

log10(3275×8194)＝log10 3275＋ log10 8194
　　　　　　　　　＝3.515211＋3.913496
　　　　　　　　　＝7.428707（＝0.428707＋7）　
  
ここで、log10 2.683533=0.428707　であることから

log10(3275×8194)＝log10 2.683533＋log10 10000000
                    　　　＝log10 26835330

これにより、3275×8194≒26835330　となる。

実際の計算結果は「26835350」なので、ほぼ正しい結果が得られている。小数点以下にさらに多くの桁数を有する常用対数表を使用すれば、より正確な数値が求められることになる。

なお、上記の基本公式に加えて、一般的ではないが、ある意味で対数の性質を示しており、その定義からよく考えてみれば成り立つことが理解できると思われる興味深い公式としては、以下のものが挙げられる。
対数の性質を示す公式

対数関数の微分・積分等

ここでは、対数関数の微分・積分に関する公式等を示しておく3。
対数関数の微分・積分に関する公式等
また、log(1+ｘ)のマクローリン展開は、以下のようになる。
マクローリン展開
 
3 対数関数の微分が「1／x」になっているということは、逆に「y-=1／x」という関数を積分する（この関数が描く曲線（直角双曲線）の面積を求める）ことで、対数が得られることになる。これにより、対数が面積という幾何学的性質に関係していることになり、それまでの計算のための概念から、数学へと進化していくことになっていった。

対数関数のグラフ

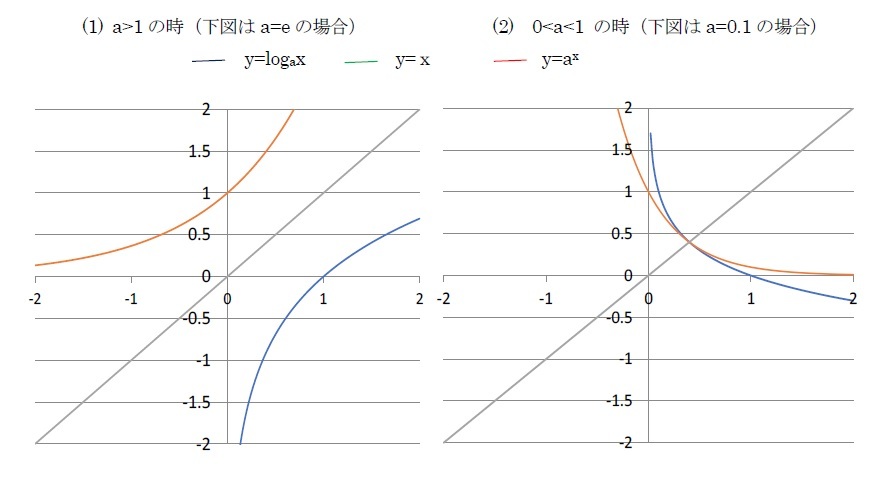
下記の図表が、対数関数y=logaxと指数関数y=ax及びｙ=xのグラフを示している。これからわかるように、

(1) 対数関数は、正の実数を定義域（x）、実数を値域（y）とする関数である。

(2) 対数関数は、a>1の時は、増加関数、0<a<1 の時は、減少関数となる。

(3) 対数関数のグラフと指数関数のグラフは、y=x に関して対称になる。
対数関数y=logaxと指数関数y=ax及びｙ=xのグラフ

片対数グラフ・両対数グラフ

上記の対数関数のグラフは、縦軸も横軸も普通目盛を使用した通常のグラフである。

これに対して、「片対数グラフ」というのは、縦軸又は横軸の一方のみが対数目盛になっていて他方は普通目盛になっているグラフをいう。また、「両対数グラフ」というのは、縦軸及び横軸の両方が対数目盛になっているグラフをいう。これらのグラフを用いることで、極めて広い範囲のデータを扱うことができることになる。

また、指数関数（y=axn）のグラフは、横軸を普通目盛（又は対数目盛）、縦軸を対数目盛にすると、直線になる。従って、指数関数に従うデータを分析する場合には、通常のグラフに比べて、対数グラフの方が回帰分析等が行いやすくなる。こうした対数グラフの利用については、別途報告することとしたい。

まとめ―対数の応用－

以上、ここまでで「対数」がどのようなものなのか、また対数に関わる基本公式等について説明してきた。それでは、この対数が実際に社会の中で、どのように利用されているのだろうか。

これについて、いくつかの例を挙げると、以下の通りとなっている。

・化石の年代測定（放射性元素の減少量に基づいて測定）
・星の明るさ　等級
・音の大きさ　dB（デシベル）
・音のラウドネス（聴覚的な強さ）　phon（ホーン）
・地震が発するエネルギーの大きさ　　マグニチュード
・水素イオン指数（酸性・アルカリ性の度合い）　pH（ペーハー）
・音階

さらには、そもそも「人間の感覚は対数感覚」であるということが言われており、有名な「ヴェーバー‐フェヒナーの法則（Weber–Fechner law）」というものも挙げられる。

これらの具体的な内容については、次回以降のこのシリーズの研究員の眼で、順次説明していくことにしたい。

(2021年06月04日「研究員の眼」)

このレポートの関連カテゴリ

Xでシェアする Facebookでシェアする
全文ダウンロード（PDF）

中村 亮一

研究・専門分野

レポートについてお問い合わせ
(取材・講演依頼)
経歴

公式SNSアカウント

新着レポートを随時お届け！
日々の情報収集にぜひご活用ください。

週間アクセスランキング

総合 領域別

更新もっと見る

ピックアップ

レポート紹介

【「対数」に、もう一度興味・関心を持ってみませんか（その１）－対数って、何だろう？－】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。

「対数」に、もう一度興味・関心を持ってみませんか（その１）－対数って、何だろう？－のレポート　Topへ