- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無理数について(その3)-無理数はどのようなところに現れてくるのか-
コラム
2022年01月04日
文字サイズ
- 小
- 中
- 大
はじめに
無理数が現れてくる状況
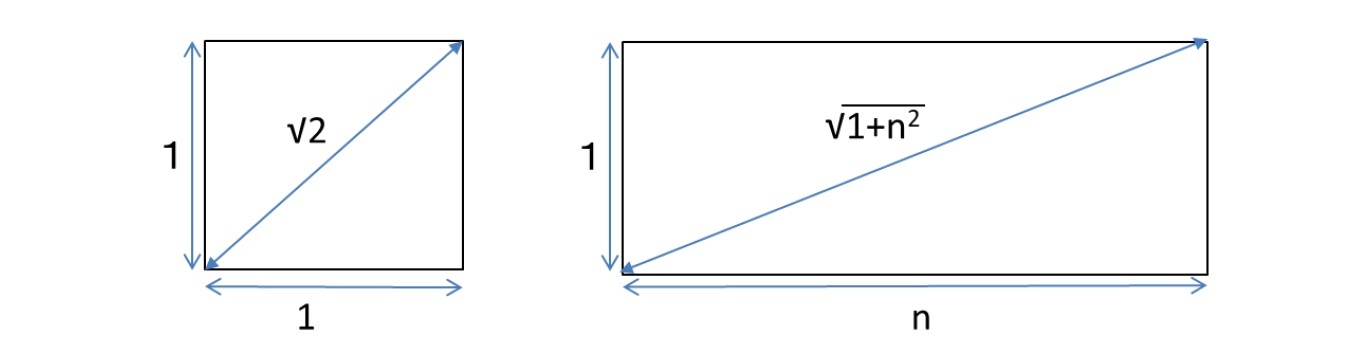
一般の方々にとって、無理数で最も有名なものとしては、√2とπ(円周率)とe(ネイピア数)が挙げられるのではないか、と思われる。
√2は、1辺が1の正方形の対角線の長さである。πは、直径が1の円周の長さである。eは、自然対数の底として、指数関数に使用されている。
ところが、無理数は他にも数多くの場面で現れてくる。以下では、これらについて紹介する。
√2は、1辺が1の正方形の対角線の長さである。πは、直径が1の円周の長さである。eは、自然対数の底として、指数関数に使用されている。
ところが、無理数は他にも数多くの場面で現れてくる。以下では、これらについて紹介する。
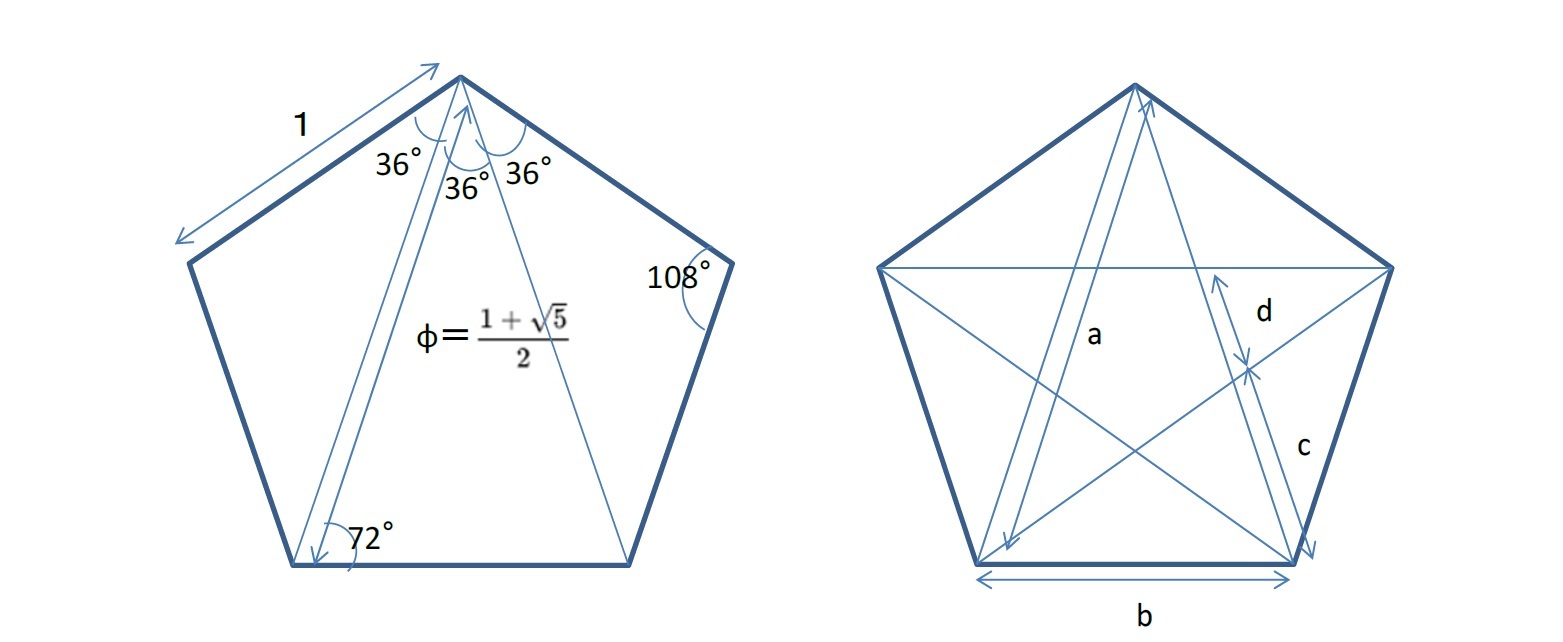
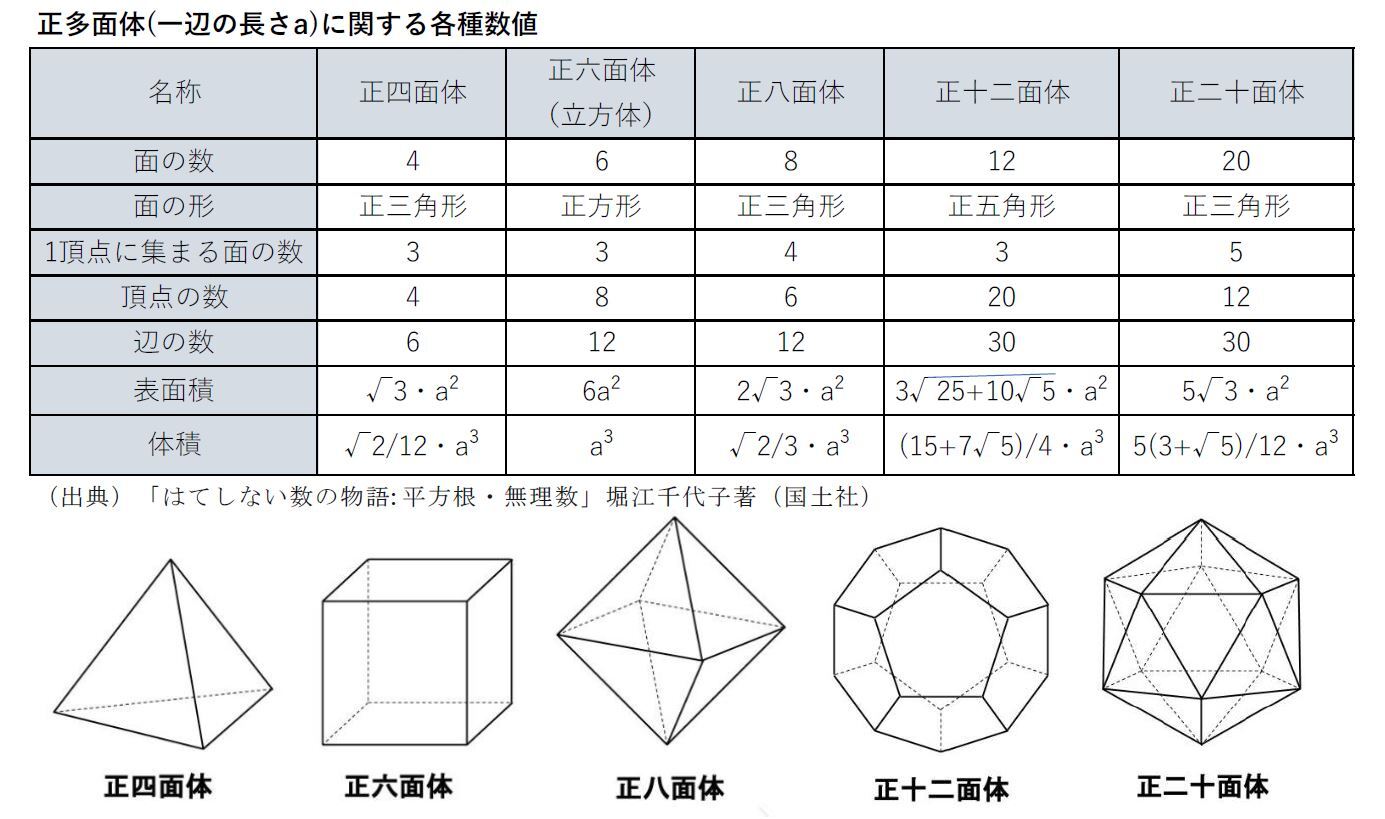
なお、研究員の眼「黄金比φについて(その1)-黄金比とはどのようなものなのか-」(2020.11.10)で報告したように、以下の「黄金比φ」も無理数である。
さらには、研究員の眼「白銀比τ等について-白銀比とはどのようなもので、どんな場面で使用されているのか-」(2020.12.14)で報告したように、以下の「白銀比τ」も無理数である。
であり、無理数の定番トリオである√2とπとeが全て含まれている。
「独立な同一の分布に従う確率変数の算術平均の分布は、元の確率変数に標準偏差が存在するならば、元の分布の形状に関係なく、変数の数が多数になったとき、正規分布に収束する」という中心極限定理により、大標本の平均値の統計では、正規分布が仮定されることが非常に多くなる。従って、正規分布は統計学上極めて重要なものとして位置付けられ、大変有用なものとなっている。
正規分布を用いることで、各種の検定や推定が行われることになる。
「独立な同一の分布に従う確率変数の算術平均の分布は、元の確率変数に標準偏差が存在するならば、元の分布の形状に関係なく、変数の数が多数になったとき、正規分布に収束する」という中心極限定理により、大標本の平均値の統計では、正規分布が仮定されることが非常に多くなる。従って、正規分布は統計学上極めて重要なものとして位置付けられ、大変有用なものとなっている。
正規分布を用いることで、各種の検定や推定が行われることになる。
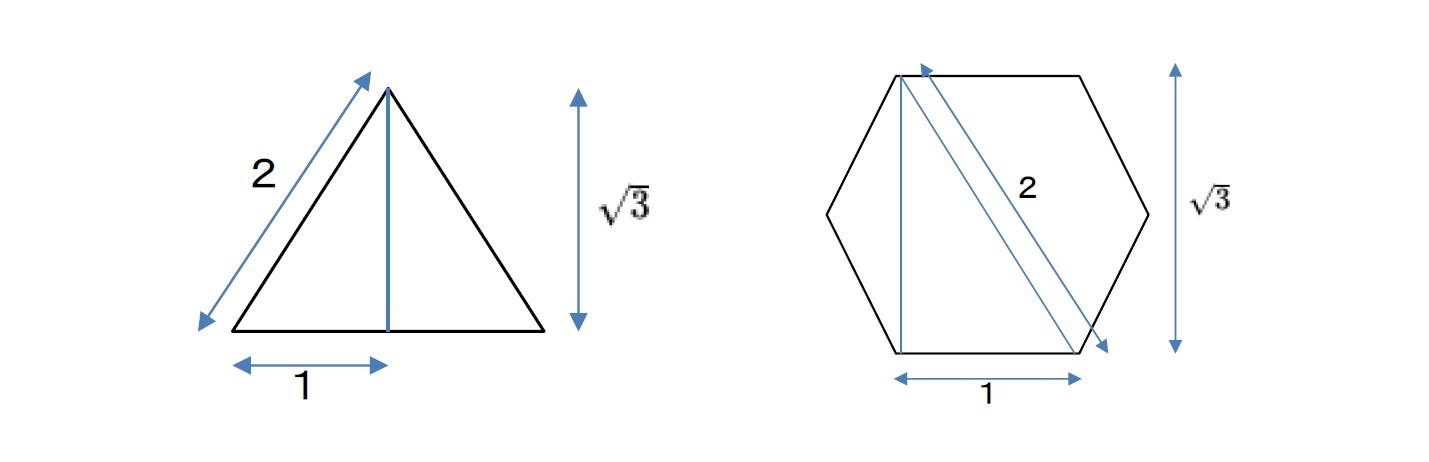
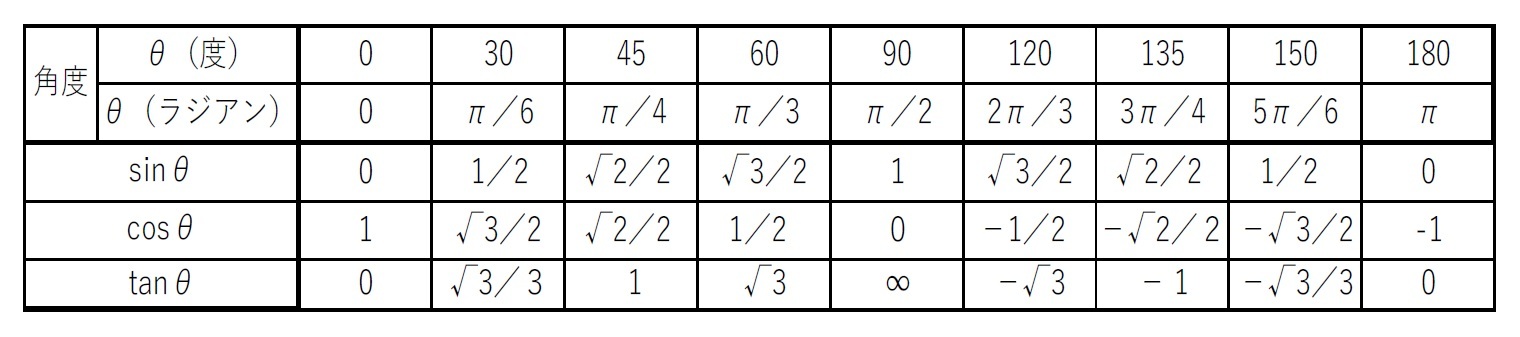
三角関数に現れる無理数
指数関数・対数関数に現れる無理数
同じく、証明等は示せないが、以下の数は超越数になっている。
・0でない代数的数aに対するea (よって、en(nは整数)は超越数である)
・0でない代数的数a、bに対するe(aπ+b)
・代数的数α(≠0、1)に対するlogα
最後の例からわかるように、対数関数で表現される数にも、無理数が溢れている形になっている。
・0でない代数的数aに対するea (よって、en(nは整数)は超越数である)
・0でない代数的数a、bに対するe(aπ+b)
・代数的数α(≠0、1)に対するlogα
最後の例からわかるように、対数関数で表現される数にも、無理数が溢れている形になっている。
ギリシアの3大作図問題
ギリシアの三大作図問題については、以前の研究員の眼「ギリシアの3大作図問題-数学を通じて、ギリシアという国の歴史的位置付けの重みを再認識してみませんか-」(2017.6.19)で報告した。
そこで述べたことを繰り返すと以下の通りとなる。
「定規とコンパスによって作図可能となるには、作図のために必要な点が、(作図可能な数で表された)1次方程式や2次方程式を繰り返し解いて得られる範囲にあることが必要で、そのような条件を満たさない点がある場合には、作図不可能ということになる。」
以上を「ギリシアの3大作図問題」に当てはめてみると、以下の通りとなる。
問題1(円積問題)
半径1の円の面積はπ(円周率)なので、この円と同じ面積を持つ正方形の1辺の長さは√π となる。πは超越数で代数的数ではないので、上記の条件を満たしていない。
問題2(立方体倍積問題)
与えられた立方体の1辺の長さを1とすると、求めたい立方体の1辺の長さXは、X3=2 ということになるが、これは3次方程式であることから、上記の条件を満たしていない。
問題3(角の3等分問題)
与えられた角をθとすると、cos(θ/3)が分かれば、そこから直線を立てて、半径1の円との交点を求めることで、角を3等分できることになる。
A=cos θ、 X=cos(θ/3)とすると、cosの3倍角の公式(高校の数学で学んだ記憶がある人もあると思われる)により、4X3-3X-A=0 となる。これも3次方程式であることから、上記の条件を満たしていない。
このように、ギリシアの3大作図問題には無理数が現れてくることになっている。
先の研究員の眼で報告したように、問題2(立方体倍積問題)と問題3(角の3等分問題)は1837年に、フランス人数学者ピエール・ローラン・ヴァンツェル(Pierre Laurent Wantzel)によって解決され、問題1(円積問題)は、1882年にドイツ人数学者フェルディナント・フォン・リンデマン(Carl Louis Ferdinand von Lindemann)によって、πの超越性の証明が行われたことで解決した。古代ギリシアの時代に素朴に感じられた問題が、2000年の時を経て、やっと解決された形になっている。
そこで述べたことを繰り返すと以下の通りとなる。
「定規とコンパスによって作図可能となるには、作図のために必要な点が、(作図可能な数で表された)1次方程式や2次方程式を繰り返し解いて得られる範囲にあることが必要で、そのような条件を満たさない点がある場合には、作図不可能ということになる。」
以上を「ギリシアの3大作図問題」に当てはめてみると、以下の通りとなる。
問題1(円積問題)
半径1の円の面積はπ(円周率)なので、この円と同じ面積を持つ正方形の1辺の長さは√π となる。πは超越数で代数的数ではないので、上記の条件を満たしていない。
問題2(立方体倍積問題)
与えられた立方体の1辺の長さを1とすると、求めたい立方体の1辺の長さXは、X3=2 ということになるが、これは3次方程式であることから、上記の条件を満たしていない。
問題3(角の3等分問題)
与えられた角をθとすると、cos(θ/3)が分かれば、そこから直線を立てて、半径1の円との交点を求めることで、角を3等分できることになる。
A=cos θ、 X=cos(θ/3)とすると、cosの3倍角の公式(高校の数学で学んだ記憶がある人もあると思われる)により、4X3-3X-A=0 となる。これも3次方程式であることから、上記の条件を満たしていない。
このように、ギリシアの3大作図問題には無理数が現れてくることになっている。
先の研究員の眼で報告したように、問題2(立方体倍積問題)と問題3(角の3等分問題)は1837年に、フランス人数学者ピエール・ローラン・ヴァンツェル(Pierre Laurent Wantzel)によって解決され、問題1(円積問題)は、1882年にドイツ人数学者フェルディナント・フォン・リンデマン(Carl Louis Ferdinand von Lindemann)によって、πの超越性の証明が行われたことで解決した。古代ギリシアの時代に素朴に感じられた問題が、2000年の時を経て、やっと解決された形になっている。
最後に
今回は、無理数がどのようなところに現れてくるのかについて報告してきた。
無理数と言われると、何か難しいものでとっつきにくいものだと感じてしまうと思われる。ところが、無理数は社会の中に満ち溢れていて、それを多くの人が、それと認識することなく利用している。また、それらの無理数の利用により、多くの恩恵を受けている。
√2もπもeも、それらが無理数であることは、数学的には重要なことで、そのためにそれを表す特別な数学記号も存在していたりする。ところが、殆どの人にとっては、これらの数を厳密に知っている必要はなく、何となくこんなものだよね、というぐらいで、√2なら1.41ぐらい、πなら3.14ぐらい、eに至ってはそのおおまかな水準すらも十分に認識されているとは思われず、ましてやこれらが無理数であることは大きな意味を有していないものと思われる。
それでも基本的には何ら問題は起こっていない。理論的には厳密な分析が行われていく必要はあるが、現実世界においては近似値や、結果だけを知っていれば、それだけで十分である。
以上、今回は3回にわたって、無理数について報告してきた。今回のレポートを契機に、無理数に少しでも親しみを持っていただければと思っている。
無理数と言われると、何か難しいものでとっつきにくいものだと感じてしまうと思われる。ところが、無理数は社会の中に満ち溢れていて、それを多くの人が、それと認識することなく利用している。また、それらの無理数の利用により、多くの恩恵を受けている。
√2もπもeも、それらが無理数であることは、数学的には重要なことで、そのためにそれを表す特別な数学記号も存在していたりする。ところが、殆どの人にとっては、これらの数を厳密に知っている必要はなく、何となくこんなものだよね、というぐらいで、√2なら1.41ぐらい、πなら3.14ぐらい、eに至ってはそのおおまかな水準すらも十分に認識されているとは思われず、ましてやこれらが無理数であることは大きな意味を有していないものと思われる。
それでも基本的には何ら問題は起こっていない。理論的には厳密な分析が行われていく必要はあるが、現実世界においては近似値や、結果だけを知っていれば、それだけで十分である。
以上、今回は3回にわたって、無理数について報告してきた。今回のレポートを契機に、無理数に少しでも親しみを持っていただければと思っている。
(2022年01月04日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる -
2025年10月24日
企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年10月24日
消費者物価(全国25年9月)-コアCPI上昇率は拡大したが、先行きは鈍化へ -
2025年10月24日
保険業界が注目する“やせ薬”?-GLP-1は死亡率改善効果をもたらすのか -
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1)
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無理数について(その3)-無理数はどのようなところに現れてくるのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無理数について(その3)-無理数はどのようなところに現れてくるのか-のレポート Topへ


















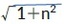


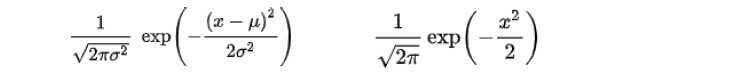

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




