- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無限について-無限に関するパラドックス(2)-
コラム
2022年08月26日
文字サイズ
- 小
- 中
- 大
はじめに
研究員の眼「無限について―無限に関するパラドックス(1)」で、有名なゼノンのパラドックスの「アキレスと亀」及び「飛んでいる矢は止まっている」について紹介し、「有限と無限」の関係、さらには「実無限と可能無限」の考え方について紹介した。これにより、「無限」の概念が極めて難しいものであるとともに、大変興味深いものであることが一定わかっていただけたのではないかと思っている。
今回は、無限に関するパラドックス(2)ということで、無限集合の濃度に関するトピック等について紹介していきたいと思っている。
今回は、無限に関するパラドックス(2)ということで、無限集合の濃度に関するトピック等について紹介していきたいと思っている。
ヒルベルトの無限ホテル
無限に関するパラドックスとして、有名なものに「ヒルベルトの無限ホテル」あるいは「ヒルベルトホテル」と呼ばれるものがある。これは次のようなものである。
無限個の客室があるホテルを考える。このホテルは「満室(即ち、全ての客室が埋まっている)」とする。これに対して、以下の3段階の新たな客の受入れを考える。
(1) 有限の客
新たに一人の客が来て、宿泊の希望をしたとする。この時、ホテルは1号室の客を2号室に、2号室の客を3号室に、n号室の客を(n+1)号室に移動させることにより、1号室に新たな客を宿泊させることができることになる。同じようなプロセスを踏むことで、新たな有限の客を受け入れることができることになる。
(2) 無限の客
新たに無限の客が来たとする。この時、ホテルは1号室の客を2号室に、2号室の客を4号室に、n号室の客を2n号室に移動させることにより、奇数号室を空けて、全ての奇数号室に新たな無限の客を宿泊させることができることになる。
(3) 無限の客を乗せた無限台のバス
新たに無限の客を乗せた無限台のバスが来たとする。この時のホテルの対応方法はいくつか考えられる。
最もよく使用されるのは、「素数冪」を用いる方法である。これは、i号室の客を2i号室に移動させて、奇数号室を開けるとともに、新たな無限台のバスの1号車のn番目の客を3n号室に、2号車のn番目の客を5n号室に、m号車のn番目の客をm番目の奇素数をpmとしてpmn号室に宿泊させるというものである。
なお、この手法に従うと、(1) や(2) のケースとは異なり、全ての素数冪ではない奇数号室は空室ということになる。これに対して、空室なく、全ての客室を埋める手法もあるが、ここでは紹介しないので、興味のある方はご自身でお調べいただければと思っている。
無限個の客室があるホテルを考える。このホテルは「満室(即ち、全ての客室が埋まっている)」とする。これに対して、以下の3段階の新たな客の受入れを考える。
(1) 有限の客
新たに一人の客が来て、宿泊の希望をしたとする。この時、ホテルは1号室の客を2号室に、2号室の客を3号室に、n号室の客を(n+1)号室に移動させることにより、1号室に新たな客を宿泊させることができることになる。同じようなプロセスを踏むことで、新たな有限の客を受け入れることができることになる。
(2) 無限の客
新たに無限の客が来たとする。この時、ホテルは1号室の客を2号室に、2号室の客を4号室に、n号室の客を2n号室に移動させることにより、奇数号室を空けて、全ての奇数号室に新たな無限の客を宿泊させることができることになる。
(3) 無限の客を乗せた無限台のバス
新たに無限の客を乗せた無限台のバスが来たとする。この時のホテルの対応方法はいくつか考えられる。
最もよく使用されるのは、「素数冪」を用いる方法である。これは、i号室の客を2i号室に移動させて、奇数号室を開けるとともに、新たな無限台のバスの1号車のn番目の客を3n号室に、2号車のn番目の客を5n号室に、m号車のn番目の客をm番目の奇素数をpmとしてpmn号室に宿泊させるというものである。
なお、この手法に従うと、(1) や(2) のケースとは異なり、全ての素数冪ではない奇数号室は空室ということになる。これに対して、空室なく、全ての客室を埋める手法もあるが、ここでは紹介しないので、興味のある方はご自身でお調べいただければと思っている。
部分と全体が同じ
無限に関するパラドックスとして、「部分と全体が同じ」というものもある。
「部分」と「全体」を比べてみた場合、殆どの人が、当然のことながら、「全体の方が部分より大きい」と考えるだろう。ところが、2つの集合の大きさの比較についてのある種の考え方では、「部分と全体が同じ」ということになる。
物の集まりである集合を考える場合に、有限集合であれば、その構成要素の個数を数えることで、2つの集合の間の大小関係を知ることができる。無限集合の場合、いずれにしても個数は無限であることから、個数による単純な大小比較はできないことになる。
そこで、無限集合を含めた2つの集合について、「2つの集合の要素の間に1対1の対応がつくときに、これらの2つの集合は同じ個数の要素を持つ(あるいは「濃度」が等しい)」とみなす、と考えることとする。より数学的な言い方をすれば、「集合Xから集合Yへの全単射が存在すれば、XとYの濃度が等しい」ということになる。「全単射(bijection mapping)」というのは、まさに「1対1対応 (one-to-one correspondence)」ができるということを意味している1。
この定義によれば、例えば、偶数全体と自然数全体Nを比較した場合に、以下のように1対1の対応が付けられることから、両者の濃度は同じ、ということになる。
「部分」と「全体」を比べてみた場合、殆どの人が、当然のことながら、「全体の方が部分より大きい」と考えるだろう。ところが、2つの集合の大きさの比較についてのある種の考え方では、「部分と全体が同じ」ということになる。
物の集まりである集合を考える場合に、有限集合であれば、その構成要素の個数を数えることで、2つの集合の間の大小関係を知ることができる。無限集合の場合、いずれにしても個数は無限であることから、個数による単純な大小比較はできないことになる。
そこで、無限集合を含めた2つの集合について、「2つの集合の要素の間に1対1の対応がつくときに、これらの2つの集合は同じ個数の要素を持つ(あるいは「濃度」が等しい)」とみなす、と考えることとする。より数学的な言い方をすれば、「集合Xから集合Yへの全単射が存在すれば、XとYの濃度が等しい」ということになる。「全単射(bijection mapping)」というのは、まさに「1対1対応 (one-to-one correspondence)」ができるということを意味している1。
この定義によれば、例えば、偶数全体と自然数全体Nを比較した場合に、以下のように1対1の対応が付けられることから、両者の濃度は同じ、ということになる。
一般的な感覚で言えば、「偶数は自然数の部分集合であり、自然数は偶数の2倍の個数があるから、自然数の方が大きい」ということになるが、上記のような考え方もできることになる。
これにより、無限の世界においては「部分と全体が同じ」になりうることになり、ある意味でこれが無限の特質の1つを示している。
無限集合の定義として、ドイツの数学者リヒャルト・デデキント(Richard Dedekind)は、「集合Xは、Xのある真部分集合X′と1対1の対応がつけられるとき、無限集合という」と定義している。この場合、無限集合でないものが有限集合となる2。
なお、無限集合の「濃度」という考え方は、ロシア(サンクトペテルブルグ)生まれのドイツの数学者ゲオルグ・カントール(Georg Cantor)によって導入された。
1 2つの集合が与えられたときに、一方の集合の各元に対し、他方の集合のただひとつの元を指定して結びつける対応のことを「写像」と呼んでいるが、「写像f:A→B が全単射である」とは、以下が成り立つことをいう。
「∀のb∊B,∃!a∊A s.t. b=f(a) 即ち、 Bに属する全てのbに対して、Aに属する唯一のaが存在してb=f(a)となる 」
2 こうした定義は、従前の、有限集合を先に定義して、有限集合でないものを無限集合とする定義と同等になる。
これにより、無限の世界においては「部分と全体が同じ」になりうることになり、ある意味でこれが無限の特質の1つを示している。
無限集合の定義として、ドイツの数学者リヒャルト・デデキント(Richard Dedekind)は、「集合Xは、Xのある真部分集合X′と1対1の対応がつけられるとき、無限集合という」と定義している。この場合、無限集合でないものが有限集合となる2。
なお、無限集合の「濃度」という考え方は、ロシア(サンクトペテルブルグ)生まれのドイツの数学者ゲオルグ・カントール(Georg Cantor)によって導入された。
1 2つの集合が与えられたときに、一方の集合の各元に対し、他方の集合のただひとつの元を指定して結びつける対応のことを「写像」と呼んでいるが、「写像f:A→B が全単射である」とは、以下が成り立つことをいう。
「∀のb∊B,∃!a∊A s.t. b=f(a) 即ち、 Bに属する全てのbに対して、Aに属する唯一のaが存在してb=f(a)となる 」
2 こうした定義は、従前の、有限集合を先に定義して、有限集合でないものを無限集合とする定義と同等になる。
整数全体の濃度も自然数全体の濃度と等しい
有理数全体の濃度も自然数全体の濃度と等しい
次に、有理数全体の濃度も自然数全体の濃度に等しい、と言われると「本当だろうか」と思われる方が多いのではないか。これについては、以下のように示される。なお、以下において、集合Xの濃度(Cardinality)をcard Xで表すことにする(|X|で表されることもある)。
ステップ1
まずは、自然数全体Nと正の有理数全体Q+の濃度が等しいことを示す。
これは、正の有理数q/p をp+q が小さい順に並べて、既約分数(pとqは1以外に公約数を持たず、これ以上約分できない分数)のみを残して、番号を振っていくと、これはQ+からNへの全単射となる。即ち、全単射f:Q+→N は、以下の通りとなる。
f(1/1)=1、f(1/2)=2、f(2/1)=3、f(1/3)=4、f(3/1)=5、f(1/4)=6、f(2/3)=7、f(3/2)=8、f(4/1)=9、f(1/5)=10、f(5/1)=11、f(1/6)=12、f(2/5)=13、f(3/4)=14、f(4/3)=15、f(5/2)=16、f(6/1)=17 ・・・
これにより、card Q+=card N となる。
ステップ2
次に、正の有理数全体Q+と有理数全体Qの濃度が等しいことを示す。
これは、先に述べた自然数と整数の濃度が同じであることを示したのと同じ考え方により、有理数全体Qが「0」と正の有理数全体Q+と負の有理数全体Q-とで構成されることから、全単射が得られ、card Q+=card Q が成り立つことになる。
あるいは、より直接的に、そもそもステップ1において、全単射f:Q→N を、以下のように定めることができる。
f(0)=1、f(1/1)=2、f(-1/1)=3、f(1/2)=4、f(-1/2)=5、f(2/1)=6、f(-2/1)=7、f(1/3)=8、f(-1/3)=9、f(3/1)=10、f(-3/1)=11、f(1/4)=12、f(-1/4)=13、f(2/3)=14、f(―2/3)=15、f(3/2)=16、f(-3/2)=17、・・・
さらには、ステップ1の結果を踏まえれば、整数全体Zが「0」と自然数(正の整数)全体Nと負の整数全体Z-で構成され、card Q+=card N、card Q-=card Z-、であることから、以下の算式が成り立つことになる。
card N = card Z = card (N∪{0}∪Z-) = card (Q+∪{0}∪Q-) = card Q
いずれにしても、card Q=card N となり、有理数全体Qと自然数全体Nの濃度は等しくなる。
ステップ1
まずは、自然数全体Nと正の有理数全体Q+の濃度が等しいことを示す。
これは、正の有理数q/p をp+q が小さい順に並べて、既約分数(pとqは1以外に公約数を持たず、これ以上約分できない分数)のみを残して、番号を振っていくと、これはQ+からNへの全単射となる。即ち、全単射f:Q+→N は、以下の通りとなる。
f(1/1)=1、f(1/2)=2、f(2/1)=3、f(1/3)=4、f(3/1)=5、f(1/4)=6、f(2/3)=7、f(3/2)=8、f(4/1)=9、f(1/5)=10、f(5/1)=11、f(1/6)=12、f(2/5)=13、f(3/4)=14、f(4/3)=15、f(5/2)=16、f(6/1)=17 ・・・
これにより、card Q+=card N となる。
ステップ2
次に、正の有理数全体Q+と有理数全体Qの濃度が等しいことを示す。
これは、先に述べた自然数と整数の濃度が同じであることを示したのと同じ考え方により、有理数全体Qが「0」と正の有理数全体Q+と負の有理数全体Q-とで構成されることから、全単射が得られ、card Q+=card Q が成り立つことになる。
あるいは、より直接的に、そもそもステップ1において、全単射f:Q→N を、以下のように定めることができる。
f(0)=1、f(1/1)=2、f(-1/1)=3、f(1/2)=4、f(-1/2)=5、f(2/1)=6、f(-2/1)=7、f(1/3)=8、f(-1/3)=9、f(3/1)=10、f(-3/1)=11、f(1/4)=12、f(-1/4)=13、f(2/3)=14、f(―2/3)=15、f(3/2)=16、f(-3/2)=17、・・・
さらには、ステップ1の結果を踏まえれば、整数全体Zが「0」と自然数(正の整数)全体Nと負の整数全体Z-で構成され、card Q+=card N、card Q-=card Z-、であることから、以下の算式が成り立つことになる。
card N = card Z = card (N∪{0}∪Z-) = card (Q+∪{0}∪Q-) = card Q
いずれにしても、card Q=card N となり、有理数全体Qと自然数全体Nの濃度は等しくなる。
実数全体の濃度は自然数全体や有理数全体の濃度よりも高い
これに対して、自然数全体Nと実数全体Rの濃度は等しくない。実数全体Rは自然数全体Nよりも濃度が高いことが、以下のように示される。
ステップ1
まずは、実数を直線で表した場合に、その直線の一部で示される「実数の一部区間」と実数が同じ濃度を有していることを示す。
具体的には、区間 (-1,1)は、実数xに対して、x/(1-x2) を対応させることで、実数全体への全単射となり、これにより、card (-1,1)=card R となる。また、区間 (0,1)は、実数xに対して、2x-1を対応させることで、区間 (-1,1)への全単射となることから、
Card (0,1)=card (-1,1)となる。これにより、card (0,1)=card R となる。
あるいは、両者を併せて、区間 (0,1)のxに対して、(1-2x)/x(x-1) を対応させることで、実数全体への全単射となり、card (0,1)=card R となる。
ステップ2
次に、自然数全体Nの濃度が区間 (0,1) の濃度と異なることを、「対角線論法」という手法を用いて背理法で証明する。
仮に、自然数全体Nから区間 (0,1) への全単射が存在したとすると、区間(0,1) の任意のn番目の数は、十進法による小数展開で、以下の形で表されることになる。
ステップ1
まずは、実数を直線で表した場合に、その直線の一部で示される「実数の一部区間」と実数が同じ濃度を有していることを示す。
具体的には、区間 (-1,1)は、実数xに対して、x/(1-x2) を対応させることで、実数全体への全単射となり、これにより、card (-1,1)=card R となる。また、区間 (0,1)は、実数xに対して、2x-1を対応させることで、区間 (-1,1)への全単射となることから、
Card (0,1)=card (-1,1)となる。これにより、card (0,1)=card R となる。
あるいは、両者を併せて、区間 (0,1)のxに対して、(1-2x)/x(x-1) を対応させることで、実数全体への全単射となり、card (0,1)=card R となる。
ステップ2
次に、自然数全体Nの濃度が区間 (0,1) の濃度と異なることを、「対角線論法」という手法を用いて背理法で証明する。
仮に、自然数全体Nから区間 (0,1) への全単射が存在したとすると、区間(0,1) の任意のn番目の数は、十進法による小数展開で、以下の形で表されることになる。
ここで、新たにn番目の数の小数点以下n桁目の数字annとは異なる数字をn桁目に置いた数字を考えると(例えば、annが奇数ならば2、偶数ならば1とすればよい)、この数字は上記で並べたどの数字とも異なるものになる(新たな数字を、既存数字のそれぞれの対角線上の数値とは異なる数値から作成していくので「対角線論法」と呼ぶ)。これは全単射であるとの前提に矛盾する。
従って、自然数全体Nから区間 (0,1) への全単射は存在せず、card N ≠card (0,1) となる。
以上より、実数全体Rの濃度は自然数全体Nの濃度とは異なり、より大きなものとなる。
これまで示してきたことにより、以下の関係が成り立つことになる。
自然数全体の濃度=整数全体の濃度=有理数全体の濃度<実数全体の濃度
card N = card Z =card Q < card R
従って、自然数全体Nから区間 (0,1) への全単射は存在せず、card N ≠card (0,1) となる。
以上より、実数全体Rの濃度は自然数全体Nの濃度とは異なり、より大きなものとなる。
これまで示してきたことにより、以下の関係が成り立つことになる。
自然数全体の濃度=整数全体の濃度=有理数全体の濃度<実数全体の濃度
card N = card Z =card Q < card R
直線と2次元平面は同じ濃度
さて、これまで述べてきたような比較は2次元の平面の世界においても行える。
例えば、以下で示すように「直線と2次元平面は同じ濃度」といえる。
これを示すには、これまでの説明でわかるように、区間 (0,1) と2次元区間 (0,1)×(0,1)の濃度が等しい、ことを示せばよい。
区間 (0,1) の任意の数は、十進法による小数展開で、以下の形で表される。
0.a1a2 ・・・ an・・・
また、同様に、2次元区間(0,1)×(0,1)の任意の数も、以下の形で表される。
(0.b1b2 ・・・ bn・・・、0.c1c2 ・・・ cn・・・)
これにより、2次元区間(0,1)×(0,1)から区間(0,1)への全単射を
(bn、cn)→ a2n-1(奇数桁)a2n(偶数桁)
として定義できる。
同様に、3次元空間も直線と同じ濃度を有している。
例えば、以下で示すように「直線と2次元平面は同じ濃度」といえる。
これを示すには、これまでの説明でわかるように、区間 (0,1) と2次元区間 (0,1)×(0,1)の濃度が等しい、ことを示せばよい。
区間 (0,1) の任意の数は、十進法による小数展開で、以下の形で表される。
0.a1a2 ・・・ an・・・
また、同様に、2次元区間(0,1)×(0,1)の任意の数も、以下の形で表される。
(0.b1b2 ・・・ bn・・・、0.c1c2 ・・・ cn・・・)
これにより、2次元区間(0,1)×(0,1)から区間(0,1)への全単射を
(bn、cn)→ a2n-1(奇数桁)a2n(偶数桁)
として定義できる。
同様に、3次元空間も直線と同じ濃度を有している。
無限集合の濃度-連続体仮説-
さて、ここまで来て、それでは「自然数全体の濃度と実数全体の濃度の間に位置する濃度を有する集合は存在するのだろうか」と疑問に思われる方もいらっしゃるかもしれない。
自然数全体の集合で代表される濃度を「可算濃度」といい、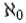 (アレフゼロあるいはアレフヌル)と表される。また、可算濃度を有する集合を「可算集合」と呼んでいる。一方で、実数全体の集合で代表される濃度を「連続体濃度」と呼んで、
(アレフゼロあるいはアレフヌル)と表される。また、可算濃度を有する集合を「可算集合」と呼んでいる。一方で、実数全体の集合で代表される濃度を「連続体濃度」と呼んで、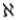 (アレフ)あるいは
(アレフ)あるいは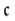 (ドイツ文字小文字の c)で表される3。実数は「非可算集合」となる。
(ドイツ文字小文字の c)で表される3。実数は「非可算集合」となる。
無限集合の濃度の中で、最も小さいものは可算濃度である。これに対して、「可算濃度の次に小さい濃度(可算濃度よりも大きい最小濃度)が連続体濃度になるのではないか」、あるいは「可算濃度と連続体濃度の間には他の濃度は存在しないのではないか」というのが、ゲオルグ・カントールによって提唱された、有名な「連続体仮説(Continuum hypothesis:CH)」である。
これに対する答えは、1963年に米国の数学者ポール・コーエン(Paul Cohen)によって「連続体仮説は、現在の数学で用いられる標準的な枠組みの下では、証明も反証(否定の証明)もできない」、つまり、「連続体仮説は数学の公理系から独立している」ということが証明されている。
自然数全体の集合で代表される濃度を「可算濃度」といい、
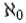 (アレフゼロあるいはアレフヌル)と表される。また、可算濃度を有する集合を「可算集合」と呼んでいる。一方で、実数全体の集合で代表される濃度を「連続体濃度」と呼んで、
(アレフゼロあるいはアレフヌル)と表される。また、可算濃度を有する集合を「可算集合」と呼んでいる。一方で、実数全体の集合で代表される濃度を「連続体濃度」と呼んで、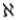 (アレフ)あるいは
(アレフ)あるいは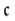 (ドイツ文字小文字の c)で表される3。実数は「非可算集合」となる。
(ドイツ文字小文字の c)で表される3。実数は「非可算集合」となる。無限集合の濃度の中で、最も小さいものは可算濃度である。これに対して、「可算濃度の次に小さい濃度(可算濃度よりも大きい最小濃度)が連続体濃度になるのではないか」、あるいは「可算濃度と連続体濃度の間には他の濃度は存在しないのではないか」というのが、ゲオルグ・カントールによって提唱された、有名な「連続体仮説(Continuum hypothesis:CH)」である。
これに対する答えは、1963年に米国の数学者ポール・コーエン(Paul Cohen)によって「連続体仮説は、現在の数学で用いられる標準的な枠組みの下では、証明も反証(否定の証明)もできない」、つまり、「連続体仮説は数学の公理系から独立している」ということが証明されている。
無限集合の濃度-一般連続体仮説-
さて、ある集合Xに対して、「その部分集合全体の集合」をXの「冪集合(べきしゅうごう)(power set」といい、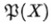 (あるいは2X )で表す4。因みに、
(あるいは2X )で表す4。因みに、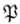 はpowerのPを表している。
はpowerのPを表している。
この時、「Xよりも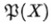 の濃度が必ず大きくなる(これを「カントールの定理」という)」ことが、これもいわゆる「対角線論法」と呼ばれる手法によって証明できる。
の濃度が必ず大きくなる(これを「カントールの定理」という)」ことが、これもいわゆる「対角線論法」と呼ばれる手法によって証明できる。
また、自然数Nの冪集合の濃度card (=card 2N)(これを
(=card 2N)(これを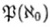 で表す)は連続体濃度
で表す)は連続体濃度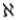 になる、ことが証明される。
になる、ことが証明される。
これらの証明はここでは示さないので、興味のある方は専門書等を参照していただきたい。
結局、これらの記号を用いると、連続体仮説というのは、

を満たすような集合Ω が存在しないという仮説、ということになる。
連続体仮説を、可算濃度と連続体濃度だけでなく、ある集合の濃度と、その冪集合の濃度に対して拡張したものを、「一般連続体仮説(generalized continuum hypothesis:GCH)」と呼んでいる。即ち、一般連続体仮説とは、無限集合 X に対し、

を満たすような 集合Ω が存在しないという仮説、のことを言う。
一般連続体仮説も、数学の公理系から独立している。
一般連続体仮説を肯定した場合、集合Xの濃度を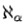 とした場合、Xの冪集合
とした場合、Xの冪集合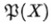 の濃度は、
の濃度は、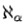 より大きい最小の濃度である
より大きい最小の濃度である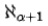 となる。
となる。
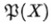 (あるいは2X )で表す4。因みに、
(あるいは2X )で表す4。因みに、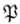 はpowerのPを表している。
はpowerのPを表している。この時、「Xよりも
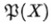 の濃度が必ず大きくなる(これを「カントールの定理」という)」ことが、これもいわゆる「対角線論法」と呼ばれる手法によって証明できる。
の濃度が必ず大きくなる(これを「カントールの定理」という)」ことが、これもいわゆる「対角線論法」と呼ばれる手法によって証明できる。また、自然数Nの冪集合の濃度card
 (=card 2N)(これを
(=card 2N)(これを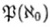 で表す)は連続体濃度
で表す)は連続体濃度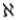 になる、ことが証明される。
になる、ことが証明される。これらの証明はここでは示さないので、興味のある方は専門書等を参照していただきたい。
結局、これらの記号を用いると、連続体仮説というのは、

を満たすような集合Ω が存在しないという仮説、ということになる。
連続体仮説を、可算濃度と連続体濃度だけでなく、ある集合の濃度と、その冪集合の濃度に対して拡張したものを、「一般連続体仮説(generalized continuum hypothesis:GCH)」と呼んでいる。即ち、一般連続体仮説とは、無限集合 X に対し、

を満たすような 集合Ω が存在しないという仮説、のことを言う。
一般連続体仮説も、数学の公理系から独立している。
一般連続体仮説を肯定した場合、集合Xの濃度を
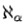 とした場合、Xの冪集合
とした場合、Xの冪集合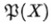 の濃度は、
の濃度は、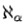 より大きい最小の濃度である
より大きい最小の濃度である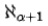 となる。
となる。
最後に
今回は、無限に関するパラドックス(2)ということで、無限の濃度に関するトピック等について紹介してきた。必ずしも厳密な言い方ができていないが、概ねの内容はこんな感じというニュアンスを感じ取ってもらえればよいのではないかと思って取り上げることにした。
いずれにしても、前回と今回の無限に関する2回のコラムで、少しは無限というものがいかに興味深いものであるのかを知って、関心を持っていただければと思っている。
いずれにしても、前回と今回の無限に関する2回のコラムで、少しは無限というものがいかに興味深いものであるのかを知って、関心を持っていただければと思っている。
(2022年08月26日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年11月04日
数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- -
2025年11月04日
ユーロ圏消費者物価(25年10月)-2%目標に沿った推移が継続 -
2025年11月04日
米国個人年金販売額は2025年上半期も過去最高記録を更新-但し保有残高純増は別の課題- -
2025年11月04日
パワーカップル世帯の動向(2)家庭と働き方~DINKS・子育て・ポスト子育て、制度と夫婦協働が支える -
2025年11月04日
「ブルー寄付」という選択肢-個人の寄付が果たす、資金流入の突破口
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無限について-無限に関するパラドックス(2)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無限について-無限に関するパラドックス(2)-のレポート Topへ





















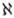
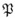

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




