- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 分数について(その1)-分数の起源等はどうなっているのか-
コラム
2023年03月28日
文字サイズ
- 小
- 中
- 大
はじめに
分数という概念は、小数の概念とは異なり、古代エジプトの時代から使用されていた。ただし、その使われ方や表記法等は、必ずしも現在と同様なものにはなっておらず、その後の経緯を経て、現在のような表記法等に至っている。
今回は、分数を巡る話題について、5回に分けて報告することにするが、今回はまずはその定義、起源、表記法等について述べることとする。
今回は、分数を巡る話題について、5回に分けて報告することにするが、今回はまずはその定義、起源、表記法等について述べることとする。
分数とは
「分数(fraction)」1は、2つの数の比で数字を表現する方法である。m(≠0)とnを整数とするとき、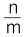 という形で表現される。
という形で表現される。
このとき、mを「分母(denominator)」、nを「分子(numerator)」と呼び、中央の線は、英語で「fraction(al) bar」と呼んでいる。これについては、日本語では「括線」とか「横線又は横棒」、さらには中国での呼び方や英語のそのままの翻訳として「分数線」というような呼び方がされているようだ1。なお、この線は、水平な線「-(horizontal bar)」だけでなく、斜めの線「/(slash/solidus)」や対角線「/(fraction slash)」でも表現される(例えば、n/m、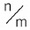 )。以下では、基本的には「n/m」方式で記載している。
)。以下では、基本的には「n/m」方式で記載している。
正の整数 m に対し 、1/m のように分子が 1 である分数を「単位分数(unit fraction)」という。
正の分数の中でも、分子が分母より小さい分数を「真分数( proper fraction)」という。真分数は 1 より小さいという性質を持つ。一方で、分子が分母より大きい分数を「仮分数(かぶんすう)(improper fraction)」という1。
また、自然数と真分数の和 k+n/mの + を省略して、k・n/m と書いた分数を「帯分数(たいぶんすう)(mixed number又はmixed numeral又はmixed fraction)」という。なお、kが負の整数、m(≠0)とnが自然数の場合、k・n/m は-(|k|+n/m)を表し、k+n/mを表しているわけではない。
なお、分子と分母が1以外の公約数を持たない整数である分数を「規約分数(irreducible fraction)」という。
また、分母や分子がさらに分数を含むような分数を「繁分数(compound fraction)」という。
さらには、以下のように、分母が数と分数の和であり、さらにその分母が数と分数の和となる形のものを「連分数(continued fraction)」という。
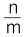 という形で表現される。
という形で表現される。このとき、mを「分母(denominator)」、nを「分子(numerator)」と呼び、中央の線は、英語で「fraction(al) bar」と呼んでいる。これについては、日本語では「括線」とか「横線又は横棒」、さらには中国での呼び方や英語のそのままの翻訳として「分数線」というような呼び方がされているようだ1。なお、この線は、水平な線「-(horizontal bar)」だけでなく、斜めの線「/(slash/solidus)」や対角線「/(fraction slash)」でも表現される(例えば、n/m、
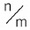 )。以下では、基本的には「n/m」方式で記載している。
)。以下では、基本的には「n/m」方式で記載している。正の整数 m に対し 、1/m のように分子が 1 である分数を「単位分数(unit fraction)」という。
正の分数の中でも、分子が分母より小さい分数を「真分数( proper fraction)」という。真分数は 1 より小さいという性質を持つ。一方で、分子が分母より大きい分数を「仮分数(かぶんすう)(improper fraction)」という1。
また、自然数と真分数の和 k+n/mの + を省略して、k・n/m と書いた分数を「帯分数(たいぶんすう)(mixed number又はmixed numeral又はmixed fraction)」という。なお、kが負の整数、m(≠0)とnが自然数の場合、k・n/m は-(|k|+n/m)を表し、k+n/mを表しているわけではない。
なお、分子と分母が1以外の公約数を持たない整数である分数を「規約分数(irreducible fraction)」という。
また、分母や分子がさらに分数を含むような分数を「繁分数(compound fraction)」という。
さらには、以下のように、分母が数と分数の和であり、さらにその分母が数と分数の和となる形のものを「連分数(continued fraction)」という。
1 英語の「fraction」とは、「端数」、「断片」という意味を有しており、ラテン語の「fractus(壊れた)」に由来しており、全体の一部を指す言葉を表している。なお、分子が整数、分母が10のべき乗の分数(十進法による有限小数)のことを「decimal fraction」という。
2 これについては、各種の意見があるようなので、ここではそれらを全て掲げさせていただいた。「括線」というのは、分数の上下を1つに括る、と言う意味合い、「横線又は横棒」は見た目のストレートな言い方、「分数線」は、英語の直訳でもあり、中国での呼び方に倣う言い方ということになる。
3 負の分数の場合も、分数の絶対値が1未満であるか、1以上であるかによって、真分数や仮分数と呼ばれる。
分数の起源
分数の起源についても、何をもって、それを起源とするのかについての問題がある。
ただし、古くから、人間は、生活の場面において、例えば食料や土地等の1つのものをいくつかに分ける必要性に直面していたことから、分数の考え方が生まれやすかった。また、分数は2つの数字の関係を比で表していたので、一般的にも理解しやすかったようである。
古代バビロニアにおいては、以前の研究員の眼「小数について(その1)-小数の起源・記法はどうなっているのか-」(2023.1.23)で説明したように、楔(くさび)型文字を使用して、「60進法の位取り記数法」で数字が記述され、十進法以外で最古の小数の概念も存在していたとされる。それらの表現の中で、その楔型文字の中に分数を表すような特別な文字も使用されていたようである。
一方で、古代エジプトにおいては、象形文字の一種であるヒエログリフ(Hieroglyph)等4を使用して、「十進法」で数字を記述していたが、位取りの考え方はなかった。その代わりに、報酬の現物支給としての食糧配分や土地の分割等の計算のための必要性から、分数の考え方が幅広く使用されていたと考えられている。
以下では、この古代エジプトにおける分数について、述べることにする。
4 古代エジプトにおいては、紀元前4000年頃から、象形文字が使用されたが、時代を経るにつれて、ヒエログリフ(神聖文字)やヒエラティック(神官文字)、さらにデモティック(民衆文字)という文字が使用されていった。
ただし、古くから、人間は、生活の場面において、例えば食料や土地等の1つのものをいくつかに分ける必要性に直面していたことから、分数の考え方が生まれやすかった。また、分数は2つの数字の関係を比で表していたので、一般的にも理解しやすかったようである。
古代バビロニアにおいては、以前の研究員の眼「小数について(その1)-小数の起源・記法はどうなっているのか-」(2023.1.23)で説明したように、楔(くさび)型文字を使用して、「60進法の位取り記数法」で数字が記述され、十進法以外で最古の小数の概念も存在していたとされる。それらの表現の中で、その楔型文字の中に分数を表すような特別な文字も使用されていたようである。
一方で、古代エジプトにおいては、象形文字の一種であるヒエログリフ(Hieroglyph)等4を使用して、「十進法」で数字を記述していたが、位取りの考え方はなかった。その代わりに、報酬の現物支給としての食糧配分や土地の分割等の計算のための必要性から、分数の考え方が幅広く使用されていたと考えられている。
以下では、この古代エジプトにおける分数について、述べることにする。
4 古代エジプトにおいては、紀元前4000年頃から、象形文字が使用されたが、時代を経るにつれて、ヒエログリフ(神聖文字)やヒエラティック(神官文字)、さらにデモティック(民衆文字)という文字が使用されていった。
古代エジプトの分数
古代エジプトの分数は、基本的に単位分数しかない。その他の分数は、幾つかの異なる単位分数の和として表される。これを「エジプト分数」又は「エジプト式分数」と呼んでいる。この形式で分数を扱う方法は、紀元前17世紀頃の古代エジプトの数学文書「リンド・パピルス」(あるいは「リンド数学パピルス(Rhind Mathematical Papyrus)」と呼ばれる)に記載されている。
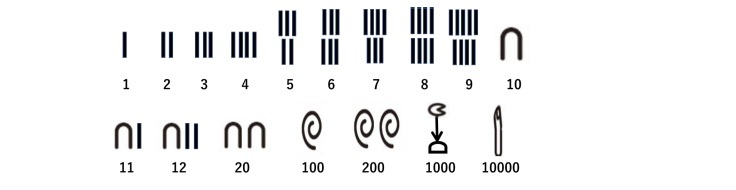
ヒエログリフの数字は十進法で、以下のような数字を表す記号を使用している(以下の記号は、あくまでもイメージを把握してもらうために、一般的に広く知られているもの等に基づいて、筆者が作成したもので、実際には各種の形が見られることには留意しておく必要がある)5。
ヒエログリフの数字は十進法で、以下のような数字を表す記号を使用している(以下の記号は、あくまでもイメージを把握してもらうために、一般的に広く知られているもの等に基づいて、筆者が作成したもので、実際には各種の形が見られることには留意しておく必要がある)5。
これらの記号が何を表しているのかについては、いろいろな解釈もあるようだが、例えば、1から9のそれぞれの垂直な棒は短い縄の一片、10はU字型の縄又は籠の取っ手、100は巻いた縄、1000は蓮の花又は睡蓮、10000は、葦かパピルスの草の芽又は指、を表しているようだ。なお、上記の図にはないが、10万はオタマジャクシ又は蛙、100万は星空に向かって手を挙げている神、1000万は太陽の形で神、を表していると言われている記号が使用されている。
具体的な数字を表す場合には、エジプト数字では桁の概念がなかったので、以下のように、1、10,100等のそれぞれの桁を表す文字を複数並べることで、各桁の数字を表していた。
具体的な数字を表す場合には、エジプト数字では桁の概念がなかったので、以下のように、1、10,100等のそれぞれの桁を表す文字を複数並べることで、各桁の数字を表していた。
リンド・パピルスについて
7 この資料は、紀元前約2000年から1800年の文書が筆写されたものとされ、ヒエラティックが使用されている。
任意の1より小さい分数は異なる単位分数の和に分解できる
となることにより、単位分数と元の数よりも小さい分子を有する分数に分解できることから、これを繰り返していくことで、有限回で単位分数に分解できることによる。ただし、いくつの単位分数の和に分解できるのかは自明でない。
また、ある分数を(異なる)単位分数の和に分解する方法の数についても、一通りではなく、複数存在している(実は、単位分数自体もさらに単位分数分解できるので、単位分数分解の方法は無限通りあることになるようだ)。
例えば、
3/ 5=1/5+ 1/3+1/15
=1/2+1/10
といような具合である。
因みに、先のリンド・パピルスの単位分数への分解が、数多くある分解方式の中から、どのような考え方に基づいて、特定の方式が選択されているのかについては、一定程度の法則が観測されているという分析等もあるようだが、必ずしも全てのケースに当てはまっているというわけでもなく、その意味では明確にはなっていないようだ。
また、ある分数を(異なる)単位分数の和に分解する方法の数についても、一通りではなく、複数存在している(実は、単位分数自体もさらに単位分数分解できるので、単位分数分解の方法は無限通りあることになるようだ)。
例えば、
3/ 5=1/5+ 1/3+1/15
=1/2+1/10
といような具合である。
因みに、先のリンド・パピルスの単位分数への分解が、数多くある分解方式の中から、どのような考え方に基づいて、特定の方式が選択されているのかについては、一定程度の法則が観測されているという分析等もあるようだが、必ずしも全てのケースに当てはまっているというわけでもなく、その意味では明確にはなっていないようだ。
(2023年03月28日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月30日
潜在成長率は変えられる-日本経済の本当の可能性 -
2025年10月30日
米FOMC(25年10月)-市場予想通り、政策金利を▲0.25%引き下げ。バランスシート縮小を12月1日で終了することも決定 -
2025年10月30日
試練の5年に踏み出す中国(後編)-「第15次五カ年計画」建議にみる、中国のこれからの針路 -
2025年10月30日
米国で進む中間期の選挙区割り変更-26年の中間選挙を見据え、与野党の攻防が激化 -
2025年10月29日
生活習慣病リスクを高める飲酒の現状と改善に向けた対策~男女の飲酒習慣の違いに着目して
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【分数について(その1)-分数の起源等はどうなっているのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
分数について(その1)-分数の起源等はどうなっているのか-のレポート Topへ


















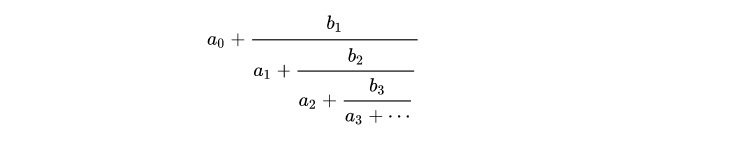

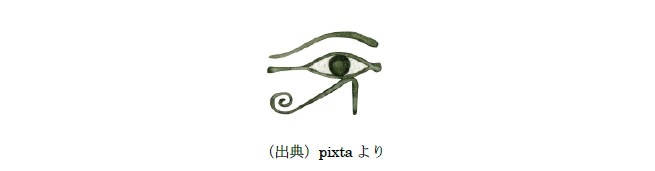
 」を用いて、表された6。
」を用いて、表された6。




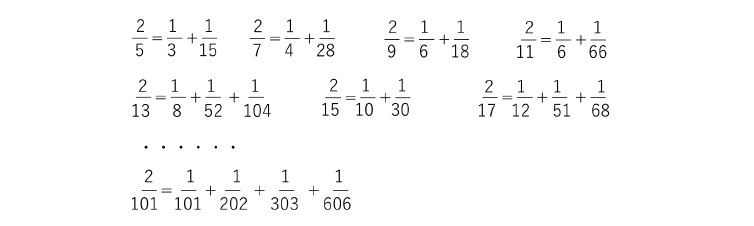


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




