- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 数学記号の由来について(6)-無限大(∞)、比例(∝)、相似(∽)等-
コラム
2020年08月07日
文字サイズ
- 小
- 中
- 大
はじめに
何回かに分けて、これまで慣れ親しんできた数学で使用されている記号の由来について、報告している1。
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等について報告した。
今回は、∞(無限大)、∝(比例する)、∽(相似)といった少し形が似ている記号及び相似との関係で≡(合同)記号の由来等について報告する。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等について報告した。
今回は、∞(無限大)、∝(比例する)、∽(相似)といった少し形が似ている記号及び相似との関係で≡(合同)記号の由来等について報告する。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
「∞」(無限大記号)の使用及び由来
「無限大(infinity)」という概念は、今や世の中に幅広く知られた概念になっており、直感的には理解されやすいものと思われるが、その数学的な定義はなかなか難しいものと思われる。「無限大」というのは、「どの実数よりも大きな数」という形で捉えられているものと思われるが、特定の数を表しているわけではなく、「いかなる数よりも大きい状態」を表しているというのがより正確ということになる。ただし、実際には、特定の数を表しているかのような形で使用されているケースも多いものと思われる。
この無限大を表す記号としての「∞」についても、いろいろな場面で出会うことがあると思われる。
この「∞」については、「ローマ数字の1000を表すↀ(CIƆ)が変化したものである。」という説が有力とされている2。以前の「数学記号の由来について(2)-数字の関係を表す記号(=、≒、<、>等)-」でも紹介したイングランドの数学者であるジョン・ウォリス(John Wallis)が最初に使用したといわれている。
「無限大」といわれても、数値の大小関係におけるプラス方向だけでなく、マイナス方向の場合もあると思われるが、この場合には正の無限大が「∞ (+∞)」で負の無限大が「−∞」と表されることになるが、一般的にはあまり御目にかかる機会はないものと思われる。
2 「ウロボロス」と呼ばれるヘビもしくは竜を図案化したものを表すために、同じ記号が使用されていたことから、これを起源とする説もあるようである。さらには、最後のギリシア文字である「ω」に基づいているとの説もあるようである。
この無限大を表す記号としての「∞」についても、いろいろな場面で出会うことがあると思われる。
この「∞」については、「ローマ数字の1000を表すↀ(CIƆ)が変化したものである。」という説が有力とされている2。以前の「数学記号の由来について(2)-数字の関係を表す記号(=、≒、<、>等)-」でも紹介したイングランドの数学者であるジョン・ウォリス(John Wallis)が最初に使用したといわれている。
「無限大」といわれても、数値の大小関係におけるプラス方向だけでなく、マイナス方向の場合もあると思われるが、この場合には正の無限大が「∞ (+∞)」で負の無限大が「−∞」と表されることになるが、一般的にはあまり御目にかかる機会はないものと思われる。
2 「ウロボロス」と呼ばれるヘビもしくは竜を図案化したものを表すために、同じ記号が使用されていたことから、これを起源とする説もあるようである。さらには、最後のギリシア文字である「ω」に基づいているとの説もあるようである。
「無限小」の概念
さらには、「無限大」の概念があるならば、当然に「無限小(infinitesimal)」の概念もある。これは、「0を除く)いかなる数よりも(その絶対値が)小さな状態」を表す概念ということになる。
例えば、ある数xが(正又は負の)無限大になるならば、1/xは無限小となることになる。
この「無限小」を表す場合には、「x→0」という記号が使用されることになる3。
3 「無限小」の概念に関連しては、ランダウの記号Landau's symbolと呼ばれる記号o (・)が重要になってくるが、ここでは触れない。なお、o(・)は"little-oh of ・"と読む。
例えば、ある数xが(正又は負の)無限大になるならば、1/xは無限小となることになる。
この「無限小」を表す場合には、「x→0」という記号が使用されることになる3。
3 「無限小」の概念に関連しては、ランダウの記号Landau's symbolと呼ばれる記号o (・)が重要になってくるが、ここでは触れない。なお、o(・)は"little-oh of ・"と読む。
「∝」(比例記号)の使用及び由来
比例関係を表す記号である「∝」は、「比例記号(proportionality symbol)」と呼ばれる。
yがxに比例していることを
y∝x
これは、別の表現をすれば、ある定数kが存在して
y=kx
と表されることを意味している。なお、
y~x
と表されることもある。
また、反比例を表す記号としては、「∝−1」を使用することもあり、
y∝−1 x
と表される。これはまた、
y∝x-1
とも表されることになり、こちらの表記の方がより一般的である。
なお、yがxに比例する時には、xもyに比例するため、「xとyは比例関係にある」とも言う。
この記号の由来についてはよくわかっていないようである。「∞」と似ていることから、無限大との関係も考えられるが、むしろ以下に述べる相似を表す記号「∽」との関係がその類似性から考えられることになる。
yがxに比例していることを
y∝x
これは、別の表現をすれば、ある定数kが存在して
y=kx
と表されることを意味している。なお、
y~x
と表されることもある。
また、反比例を表す記号としては、「∝−1」を使用することもあり、
y∝−1 x
と表される。これはまた、
y∝x-1
とも表されることになり、こちらの表記の方がより一般的である。
なお、yがxに比例する時には、xもyに比例するため、「xとyは比例関係にある」とも言う。
この記号の由来についてはよくわかっていないようである。「∞」と似ていることから、無限大との関係も考えられるが、むしろ以下に述べる相似を表す記号「∽」との関係がその類似性から考えられることになる。
「∽」(相似記号)の使用と由来
「相似(similarity)」とは、「一つの図形を拡大または縮小した関係にあること」を指している。この相似関係を表す記号「∽」については、相似や類似していることを意味するラテン語の「similis」(あるいは英語の「similar」)の頭文字Sを横にしたものといわれている。
具体的には、これまでの説明でも参考にさせていただいた米国の数学者、数学史家のフロリアン・カジョリ(Florian Cajori)の文献4によれば、ゴットフリート・ウィルヘルム・ライプニッツ(Gottfried Wilhelm Leibniz)が、1679年の未発表の原稿「Characteristica Geometrica」の中で、aとbが相似であることを「a~b」で表現したとされている。ここで、この段階では「~」であって、「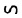 」ではなかったが、その後、ライプニッツは「
」ではなかったが、その後、ライプニッツは「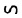 」も使用したようで、両方の記号がその後も現代まで使用されてきているようである。
」も使用したようで、両方の記号がその後も現代まで使用されてきているようである。
なお、欧米では、相似関係を表すのに「~」が一般的に使用されているようである。
4 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications Inc.)
具体的には、これまでの説明でも参考にさせていただいた米国の数学者、数学史家のフロリアン・カジョリ(Florian Cajori)の文献4によれば、ゴットフリート・ウィルヘルム・ライプニッツ(Gottfried Wilhelm Leibniz)が、1679年の未発表の原稿「Characteristica Geometrica」の中で、aとbが相似であることを「a~b」で表現したとされている。ここで、この段階では「~」であって、「
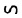 」ではなかったが、その後、ライプニッツは「
」ではなかったが、その後、ライプニッツは「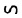 」も使用したようで、両方の記号がその後も現代まで使用されてきているようである。
」も使用したようで、両方の記号がその後も現代まで使用されてきているようである。なお、欧米では、相似関係を表すのに「~」が一般的に使用されているようである。
4 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications Inc.)
「≡」(合同記号)の使用と由来
「合同(congruence)」とは、幾何学,整数論などで使われる用語である。
(1) 幾何学での合同
2つの図形AとBが,移動によって重ね合せられるとき、AとBは合同であるといい、A≡B と書く。この意味での「合同」はまさに、相似の特別なケースに相当することになる。
(2) 整数論での合同
2つの整数 a ,b があって,a-b が m で割り切れるとき,a ,b は m を法として合同(a は b に mod m で合同)であるといい,記号で a≡b(mod m) と書く。
(1) 幾何学での合同記号
幾何学における合同記号「≡」(3本線)については、欧米で使用されている相似を表す記号「~」に対して、等しいことを意味する「=」としての「-」を付けて、さらに「=」と区別するために「≡」になったと言われている。
同じくフロリアン・カジョリ(Florian Cajori)の文献によれば、概ね以下のように記述されている。
合同のための記号を最初に導入したのは、相似記号と同じく、ゴットフリート・ウィルヘルム・ライプニッツ(Gottfried Wilhelm Leibniz)で、彼は、1679年の未発表の原稿で、図形の合同を表す目的で、「~」の下に「-」をつけた記号「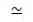 」を使用した。なお、 ライプニッツの合同記号が印刷版で最初に登場したのは、1710年のMiscellanea Berolinensiaの中のライプニッツによるとされている匿名の記事「Monitum」においてだった。この時には「
」を使用した。なお、 ライプニッツの合同記号が印刷版で最初に登場したのは、1710年のMiscellanea Berolinensiaの中のライプニッツによるとされている匿名の記事「Monitum」においてだった。この時には「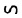 」の下に「-」を付けた記号が使用されていたようである。
」の下に「-」を付けた記号が使用されていたようである。
1717年には、クリスティアン・フォン・ヴォルフ(Christian von Wolff)が、「= et ~」と書き表している。
1777年には、ヨハン・フリードリッヒ・ハセラー(Johann Friedrich Haseler)が、Anfangsgründe der Arith., Alg., Geom. und Trig(Lemgo)、Elementar-Geometrieで、=の上に「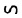 」を付けた記号を使用した。
」を付けた記号を使用した。
1824年には、カール・ブランダン・モルワイデ(Carl Brandan Mollweide)が、ユークリッドのElementeで、「=」の上に「~」をつけた「≅」を使用した。
一方で、「≡」の使用については、ハンガリーの数学者ファルカシュ・ヴォルフガング・ボヤイ(Farkas Wolfgang Bolyai)の1897年の著書等、19世紀後半から20世紀初頭にかけて、数多くの数学者によって使用された。
現在、多くの国で、合同記号として「≅」が使用されており、日本において使用されている「≡」は、英国でも幅広く使用されているようではあるが、世界においては少数派となっているようだ。
(2) 整数論での合同記号
一方で、整数論においては、ヨハン・カール・フリードリヒ・ガウス(Johann Carl Friedrich Gauß)が、1801年に「Disquisitiones Arithmeticae」で数の合同の記号として使用した。
(1) 幾何学での合同
2つの図形AとBが,移動によって重ね合せられるとき、AとBは合同であるといい、A≡B と書く。この意味での「合同」はまさに、相似の特別なケースに相当することになる。
(2) 整数論での合同
2つの整数 a ,b があって,a-b が m で割り切れるとき,a ,b は m を法として合同(a は b に mod m で合同)であるといい,記号で a≡b(mod m) と書く。
(1) 幾何学での合同記号
幾何学における合同記号「≡」(3本線)については、欧米で使用されている相似を表す記号「~」に対して、等しいことを意味する「=」としての「-」を付けて、さらに「=」と区別するために「≡」になったと言われている。
同じくフロリアン・カジョリ(Florian Cajori)の文献によれば、概ね以下のように記述されている。
合同のための記号を最初に導入したのは、相似記号と同じく、ゴットフリート・ウィルヘルム・ライプニッツ(Gottfried Wilhelm Leibniz)で、彼は、1679年の未発表の原稿で、図形の合同を表す目的で、「~」の下に「-」をつけた記号「
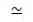 」を使用した。なお、 ライプニッツの合同記号が印刷版で最初に登場したのは、1710年のMiscellanea Berolinensiaの中のライプニッツによるとされている匿名の記事「Monitum」においてだった。この時には「
」を使用した。なお、 ライプニッツの合同記号が印刷版で最初に登場したのは、1710年のMiscellanea Berolinensiaの中のライプニッツによるとされている匿名の記事「Monitum」においてだった。この時には「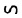 」の下に「-」を付けた記号が使用されていたようである。
」の下に「-」を付けた記号が使用されていたようである。1717年には、クリスティアン・フォン・ヴォルフ(Christian von Wolff)が、「= et ~」と書き表している。
1777年には、ヨハン・フリードリッヒ・ハセラー(Johann Friedrich Haseler)が、Anfangsgründe der Arith., Alg., Geom. und Trig(Lemgo)、Elementar-Geometrieで、=の上に「
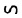 」を付けた記号を使用した。
」を付けた記号を使用した。1824年には、カール・ブランダン・モルワイデ(Carl Brandan Mollweide)が、ユークリッドのElementeで、「=」の上に「~」をつけた「≅」を使用した。
一方で、「≡」の使用については、ハンガリーの数学者ファルカシュ・ヴォルフガング・ボヤイ(Farkas Wolfgang Bolyai)の1897年の著書等、19世紀後半から20世紀初頭にかけて、数多くの数学者によって使用された。
現在、多くの国で、合同記号として「≅」が使用されており、日本において使用されている「≡」は、英国でも幅広く使用されているようではあるが、世界においては少数派となっているようだ。
(2) 整数論での合同記号
一方で、整数論においては、ヨハン・カール・フリードリヒ・ガウス(Johann Carl Friedrich Gauß)が、1801年に「Disquisitiones Arithmeticae」で数の合同の記号として使用した。
「≡」のその他の使用例
なお、記号「≡」は、その他に以下のような意味でも使用されている。
恒等式(identity)
左辺と右辺が常に等しい「恒等式」を表すために、リーマン予想やリーマン積分で有名なゲオルク・フリードリヒ・ベルンハルト・リーマン(Georg Friedrich Bernhard Riemann)が1899年に『楕円関数論』で使用した。
定義
左辺を右辺の式で定義するときに使う。
同値
論理学では両方の真偽が一致しているという意味での「同値」を表している。E・H・ムーアや、アルフレッド・ノース・ホワイトヘッド(Alfred North Whitehead)とバートランド・アーサー・ウィリアム・ラッセル(Bertrand Arthur William Russell)が、1910年に使用した。
恒等式(identity)
左辺と右辺が常に等しい「恒等式」を表すために、リーマン予想やリーマン積分で有名なゲオルク・フリードリヒ・ベルンハルト・リーマン(Georg Friedrich Bernhard Riemann)が1899年に『楕円関数論』で使用した。
定義
左辺を右辺の式で定義するときに使う。
同値
論理学では両方の真偽が一致しているという意味での「同値」を表している。E・H・ムーアや、アルフレッド・ノース・ホワイトヘッド(Alfred North Whitehead)とバートランド・アーサー・ウィリアム・ラッセル(Bertrand Arthur William Russell)が、1910年に使用した。
最後に
今回は、∞(無限大)、∝(比例する)、∽(相似)といった少し形が似ている記号及び相似との関係で≡(合同)記号の由来等について報告してきた。
結局、これらの記号も、これまでよく見られたように、基本的にはそれを表す用語の頭文字等に由来しているケースが多いようである。味気ないといってしまえば、それまでだが、ある意味ではその方が一般にも受け入れやすいということもあるのだろう。
さらには、同じ「≡」という記号が様々な意味合いで使用されていることも紹介した。もちろん、使用されている領域が異なっているので、誤解されることはない。
さらには、再び、日本で使用されている記号が必ずしも国際的に標準的なものとは限らないことを報告した。これについても、それぞれが事実を認識していれば混乱することはないだろう。それでもせめて数学のような世界では、できる限り世界共通の記号を使用していただきたいと感じた次第である。
結局、これらの記号も、これまでよく見られたように、基本的にはそれを表す用語の頭文字等に由来しているケースが多いようである。味気ないといってしまえば、それまでだが、ある意味ではその方が一般にも受け入れやすいということもあるのだろう。
さらには、同じ「≡」という記号が様々な意味合いで使用されていることも紹介した。もちろん、使用されている領域が異なっているので、誤解されることはない。
さらには、再び、日本で使用されている記号が必ずしも国際的に標準的なものとは限らないことを報告した。これについても、それぞれが事実を認識していれば混乱することはないだろう。それでもせめて数学のような世界では、できる限り世界共通の記号を使用していただきたいと感じた次第である。
本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2020年08月07日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月28日
試練の5年に踏み出す中国(前編)-「第15次五カ年計画」の5年間は、どのような5年か -
2025年10月28日
地域医療連携推進法人の現状と今後を考える-「連携以上、統合未満」で協力する形態、その将来像は? -
2025年10月28日
東宝の自己株式取得-公開買付による取得 -
2025年10月28日
今週のレポート・コラムまとめ【10/21-10/27発行分】 -
2025年10月27日
大学卒女性の働き方別生涯賃金の推計(令和6年調査より)-正社員で2人出産・育休・時短で2億円超
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【数学記号の由来について(6)-無限大(∞)、比例(∝)、相似(∽)等-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数学記号の由来について(6)-無限大(∞)、比例(∝)、相似(∽)等-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




