- シンクタンクならニッセイ基礎研究所 >
- 数学記号の由来について(3)-集合論で使用される記号(⊃、⊂、∩、∪等)-
コラム
2020年01月07日
文字サイズ
- 小
- 中
- 大
はじめに
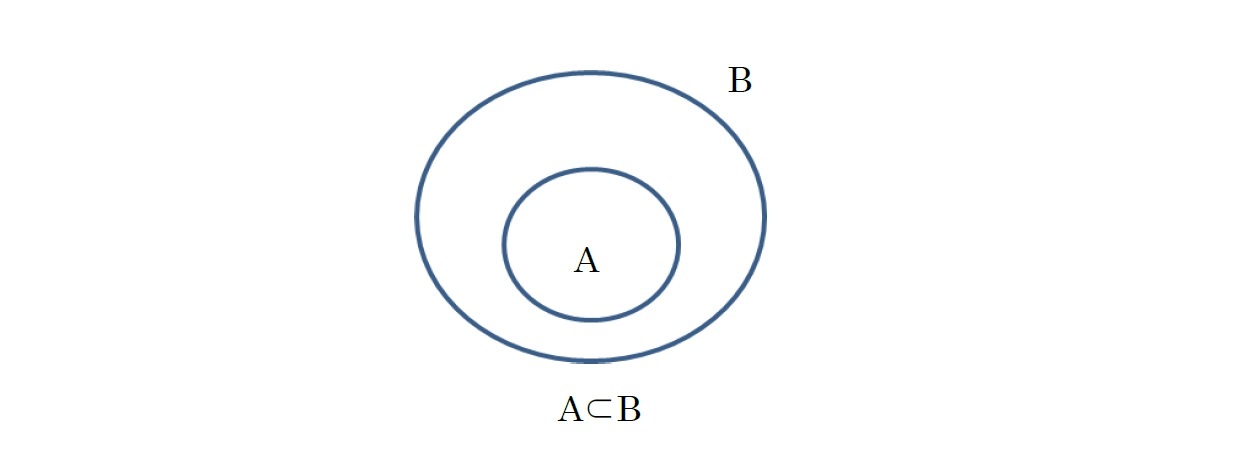
「⊂」及び「⊃」(含む、含まれる)部分集合、包含関係を表す記号の使用及び由来
初期の集合論を築いたのは、ロシアの数学者であるゲオルク・カントール(Georg Cantor)とドイツの数学者であるリヒャルト・デデキント(Richard Dedekind)、さらには彼らに続くイタリアの数学者であるジュゼッペ・ペアノ(Giuseppe Peano)等であるが、デデキントの1872年の著作「数について」において、「⊂」の記号が使用されている。
この記号について、脚注に掲げたフロリアン・カジョーリ(Florian Cajori)の著書によれば、1890年のエルンスト・シュレーダー(Ernst Schröder)による「Vorlesungen über die Algebra der Logik(論理代数に関する講義)」において導入された、となっている。それ以前は、「<」や「>」の記号が使用されていたとのことである。
一方で、ポール・テーラー(Paul Taylor)のWeb Page2によれば、「(フランスの数学者、論理学者である)ジョセフ・ゲルゴンヌ(Joseph Gergonne)が、1817年に「contient(フランス語で「含まれている」)」の意味での「C」及びその逆として「⊃」を使用したとし、これらの記号がペアノやバートランド・ラッセル(Bertrand Russell)やアルフレッド・ノース・ホワイトヘッド (Alfred North Whitehead)によっても使用されていった」とのことである。
このように、「⊂」の記号は、「含む」という表現言語の頭文字や不等号との関係で自然と考え出されてきたようである。
なお、その他の記号としては、「⊆」、「⊇」、「⊊」、「⊋」等がある。
「A⊆B」は、「AはBに含まれる」(ただし、A=Bの場合も含まれる)ことを表す。A=Bの場合を排除したい場合には、「A⊊B」と表されることになる。この場合、「AはBの真部分集合である」と呼ばれる。
なお、これらの記号を否定する場合として、「⊄」、「⊅」、「⊈」。「⊉」のような記号も存在している。
この記号について、脚注に掲げたフロリアン・カジョーリ(Florian Cajori)の著書によれば、1890年のエルンスト・シュレーダー(Ernst Schröder)による「Vorlesungen über die Algebra der Logik(論理代数に関する講義)」において導入された、となっている。それ以前は、「<」や「>」の記号が使用されていたとのことである。
一方で、ポール・テーラー(Paul Taylor)のWeb Page2によれば、「(フランスの数学者、論理学者である)ジョセフ・ゲルゴンヌ(Joseph Gergonne)が、1817年に「contient(フランス語で「含まれている」)」の意味での「C」及びその逆として「⊃」を使用したとし、これらの記号がペアノやバートランド・ラッセル(Bertrand Russell)やアルフレッド・ノース・ホワイトヘッド (Alfred North Whitehead)によっても使用されていった」とのことである。
このように、「⊂」の記号は、「含む」という表現言語の頭文字や不等号との関係で自然と考え出されてきたようである。
なお、その他の記号としては、「⊆」、「⊇」、「⊊」、「⊋」等がある。
「A⊆B」は、「AはBに含まれる」(ただし、A=Bの場合も含まれる)ことを表す。A=Bの場合を排除したい場合には、「A⊊B」と表されることになる。この場合、「AはBの真部分集合である」と呼ばれる。
なお、これらの記号を否定する場合として、「⊄」、「⊅」、「⊈」。「⊉」のような記号も存在している。
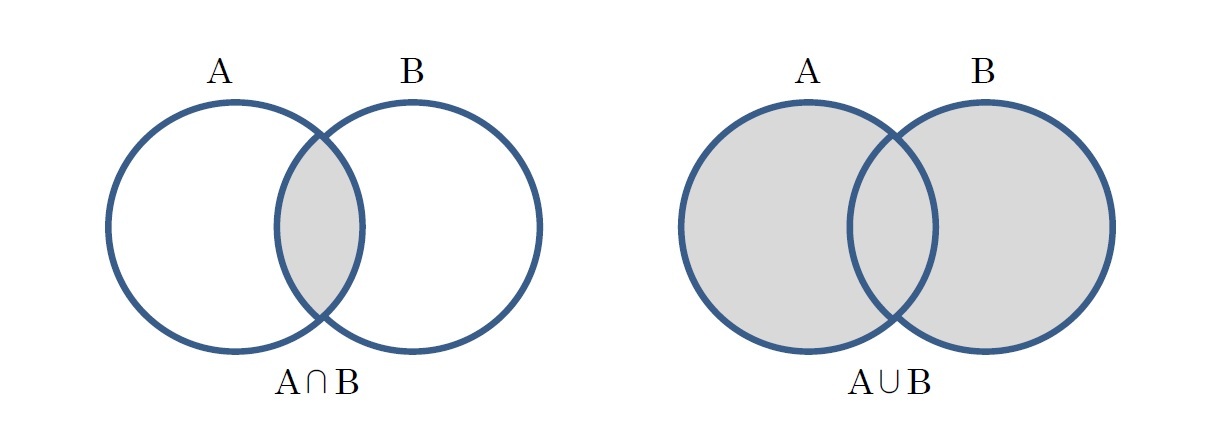
「∩」、「∪」記号の使用及び由来
これらの記号については、ペアノが1888年の論文「Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann(H. Grassmannの広延論による幾何学的計算)」で最初に使用したとされている。
「∪」はunionの頭文字からきており、「∩」は「∪」との対比で使用されたと考えられている。
なお、「∪」はカップ(cup)、「∩」は「キャップ(cap)(帽子)」とも呼ばれており、実際に文字変換ソフト等では、こうした名称の入力によって、該当の記号を呼び出すことができる。
「∪」はunionの頭文字からきており、「∩」は「∪」との対比で使用されたと考えられている。
なお、「∪」はカップ(cup)、「∩」は「キャップ(cap)(帽子)」とも呼ばれており、実際に文字変換ソフト等では、こうした名称の入力によって、該当の記号を呼び出すことができる。
「∋」(要素(元)として含む)、「∈」(属する)記号の使用及び由来
Aを集合とし、xをある要素(元)とした場合に、「x∈A」は、「xはAに含まれる」ことを意味し、「xはAの要素(元)である」又は「xはAに属する」と呼ばれる。英語では「set membership」と呼ばれる記号で、まさに「x is an element of A」という呼び方となる。
同じ内容を意味している場合でも、「A∋x」とすると、「Aはxを含む」又は「Aはxを要素(元)として含む」と呼ばれ、英語では「A contains x as an element」と呼ばれることになる。
先に書かれるものが主語になる形で呼ばれるが、実質的な意味合いの差はない。
ペアノは、1889年の「Arithmetices prinicipia nova methodo exposita(新しい方法の算術原理の説明)」の中で、要素を表すために「ε」を使用した。彼はそれを「est」の略語であると述べたとのことである。ただし、ペアノの記号はアンシャル体(uncial script)3のエプシロン(あるいはイプシロン)であり、現在使用されている定型化されたエプシロンではなかったようだ。
現在の定型化されたエプシロンは、イギリスの哲学者、論理学者、数学者であり、社会批評家、政治活動家でもあったバートランド・ラッセル(Bertrand Russell)が1903年に「Principles of Mathematicsin(数学の原理)」の中で使用したようだ。ただし、ラッセルによれば彼はペアノの記号を使用したと述べており、実際にそのように見え、現代的なエプシロンの使用を意図してはいなかったようだ。ペアノは、1889年の「I Principii di geometria logicamente esposti(論理的に公開された幾何原則)」の中でより一般的なエプシロンを使用していた。
また、これらの記号を否定する場合として、「∌」、「∉」という記号も存在しているが、これらについては、1939年にニコラ・ブルバキ(Nicolas Bourbaki)4の「Theorie des ensembles(集合論)」の中で、初めて使用されたようだ。
3 西暦4世紀から8世紀にかけてラテン語とギリシャ語の写本に使われた大文字の書体
4 ニコラ・ブルバキ(Nicolas Bourbaki)は架空の数学者であり、主にフランスの若手の数学者集団のペンネームである..
同じ内容を意味している場合でも、「A∋x」とすると、「Aはxを含む」又は「Aはxを要素(元)として含む」と呼ばれ、英語では「A contains x as an element」と呼ばれることになる。
先に書かれるものが主語になる形で呼ばれるが、実質的な意味合いの差はない。
ペアノは、1889年の「Arithmetices prinicipia nova methodo exposita(新しい方法の算術原理の説明)」の中で、要素を表すために「ε」を使用した。彼はそれを「est」の略語であると述べたとのことである。ただし、ペアノの記号はアンシャル体(uncial script)3のエプシロン(あるいはイプシロン)であり、現在使用されている定型化されたエプシロンではなかったようだ。
現在の定型化されたエプシロンは、イギリスの哲学者、論理学者、数学者であり、社会批評家、政治活動家でもあったバートランド・ラッセル(Bertrand Russell)が1903年に「Principles of Mathematicsin(数学の原理)」の中で使用したようだ。ただし、ラッセルによれば彼はペアノの記号を使用したと述べており、実際にそのように見え、現代的なエプシロンの使用を意図してはいなかったようだ。ペアノは、1889年の「I Principii di geometria logicamente esposti(論理的に公開された幾何原則)」の中でより一般的なエプシロンを使用していた。
また、これらの記号を否定する場合として、「∌」、「∉」という記号も存在しているが、これらについては、1939年にニコラ・ブルバキ(Nicolas Bourbaki)4の「Theorie des ensembles(集合論)」の中で、初めて使用されたようだ。
3 西暦4世紀から8世紀にかけてラテン語とギリシャ語の写本に使われた大文字の書体
4 ニコラ・ブルバキ(Nicolas Bourbaki)は架空の数学者であり、主にフランスの若手の数学者集団のペンネームである..
空集合「∅」(これは、φ(ファイ)じゃない)記号の使用及び由来
「∅」は、「空集合(集合を構成する要素がない)(empty set)」を表している。この「∅」という記号は、形の似ているギリシャ文字の「φ(ファイ)」とは異なるものである。Microsoft Wordでは、「∅」は、「記号と特殊記号」の一覧から選択することができる。
「∅」は、ニコラ・ブルバキの1939年の「Éléments de mathématique Fasc.1: Les structures fondamentales de l'analyse; Liv.1: Theorie de ensembles. (Fascicule de resultants) (数学の要素Fasc.1:分析の基本構造 Liv.1:集合論 (結果の束))」の中で、初めて使用された。フランスの数学者であるアンドレ・ヴェイユ(André Weil)は、その自伝の中で、「∅」の使用は自分に責任があり、これはノルウェー語等で用いられるアルファベット Ø に由来している、と述べている。
なお、空集合は、{ } で表されることもある。
また、空集合は数字の「0」と類似の概念であることから、数字の「0」に「/(スラッシュ)」を加えて、タイプライターによる重ね打ちで表現できる「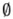 」(slashed zero)も使用されてきた。これらの「
」(slashed zero)も使用されてきた。これらの「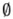 」や「φ」を「∅」の代わりに、代替的に使用することについては、(本来的なものではないが)実質的には認められてきているようである。
」や「φ」を「∅」の代わりに、代替的に使用することについては、(本来的なものではないが)実質的には認められてきているようである。
「∅」は、ニコラ・ブルバキの1939年の「Éléments de mathématique Fasc.1: Les structures fondamentales de l'analyse; Liv.1: Theorie de ensembles. (Fascicule de resultants) (数学の要素Fasc.1:分析の基本構造 Liv.1:集合論 (結果の束))」の中で、初めて使用された。フランスの数学者であるアンドレ・ヴェイユ(André Weil)は、その自伝の中で、「∅」の使用は自分に責任があり、これはノルウェー語等で用いられるアルファベット Ø に由来している、と述べている。
なお、空集合は、{ } で表されることもある。
また、空集合は数字の「0」と類似の概念であることから、数字の「0」に「/(スラッシュ)」を加えて、タイプライターによる重ね打ちで表現できる「
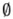 」(slashed zero)も使用されてきた。これらの「
」(slashed zero)も使用されてきた。これらの「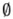 」や「φ」を「∅」の代わりに、代替的に使用することについては、(本来的なものではないが)実質的には認められてきているようである。
」や「φ」を「∅」の代わりに、代替的に使用することについては、(本来的なものではないが)実質的には認められてきているようである。
その他の集合関係の記号について
「A\B」又は「A-B」
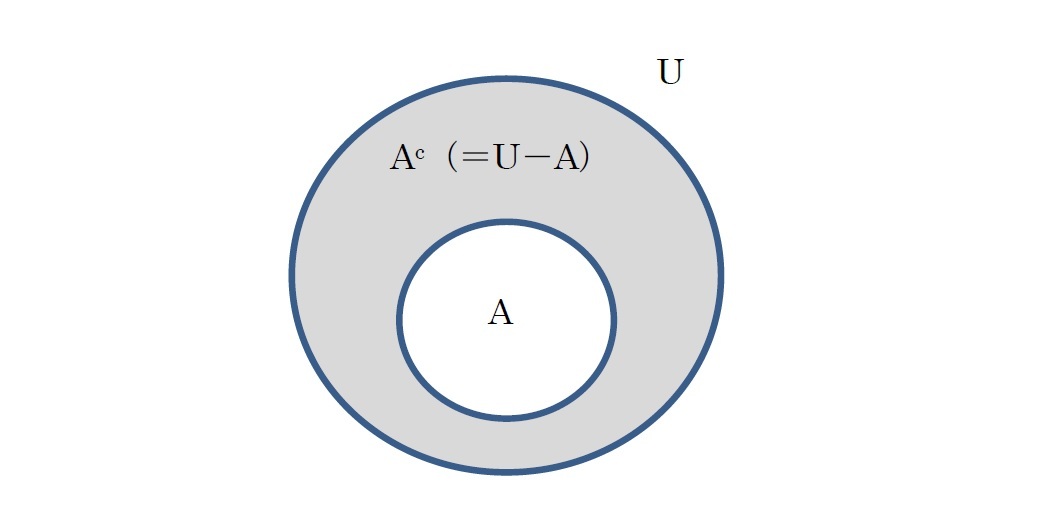
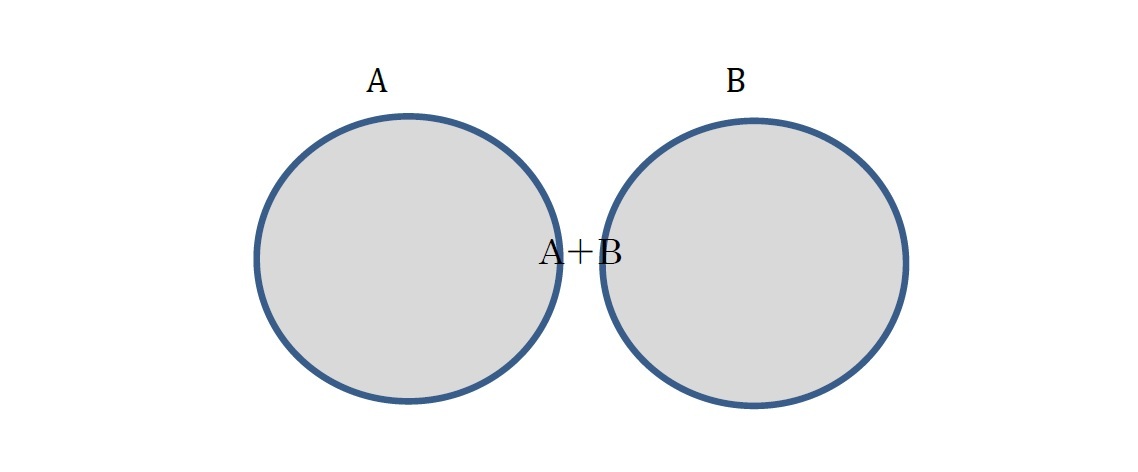
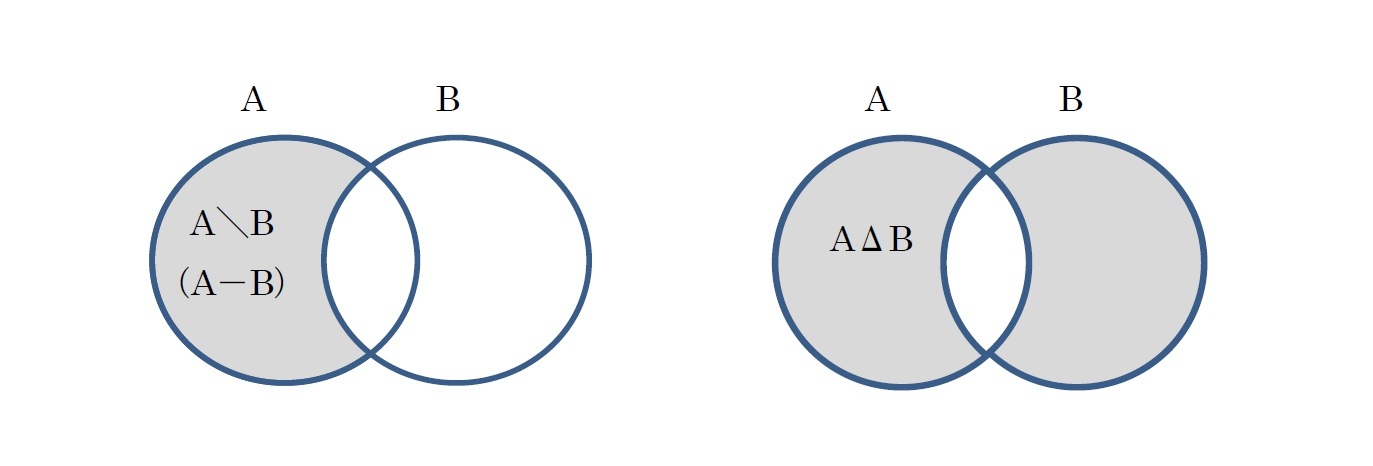
「A\B」又は「A-B」は、A に含まれているが Bには含まれていない要素(元)の集合を表しており、「差集合」と呼ばれる。A∩Bcとも表現できる。
「A\B」又は「A-B」は、A に含まれているが Bには含まれていない要素(元)の集合を表しており、「差集合」と呼ばれる。A∩Bcとも表現できる。
|A|
|A| は、集合 Aの濃度(Aが有限集合の場合,要素の個数)を表している。
|A| は、集合 Aの濃度(Aが有限集合の場合,要素の個数)を表している。
最後に
今回は、我々が学生時代に学んだ「集合」で使用される記号の使用及びそれらの由来について報告してきた。
今回の「集合」で使用される記号については、結構その意味するところの表現言語の頭文字に由来しているものが多いことがわかる。こうした傾向は、今後報告するその他の数学記号の由来においてもかなり見られる傾向となっており、ある意味で自然なものとなっている。
今回の「集合」で使用される記号については、結構その意味するところの表現言語の頭文字に由来しているものが多いことがわかる。こうした傾向は、今後報告するその他の数学記号の由来においてもかなり見られる傾向となっており、ある意味で自然なものとなっている。
(2020年01月07日「研究員の眼」)
このレポートの関連カテゴリ
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる -
2025年10月24日
企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年10月24日
消費者物価(全国25年9月)-コアCPI上昇率は拡大したが、先行きは鈍化へ -
2025年10月24日
保険業界が注目する“やせ薬”?-GLP-1は死亡率改善効果をもたらすのか -
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1)
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【数学記号の由来について(3)-集合論で使用される記号(⊃、⊂、∩、∪等)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数学記号の由来について(3)-集合論で使用される記号(⊃、⊂、∩、∪等)-のレポート Topへ


















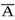

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




