- シンクタンクならニッセイ基礎研究所 >
- 数学記号の由来について(2)-数字の関係を表す記号(=、≒、<、>等)-
コラム
2019年10月04日
文字サイズ
- 小
- 中
- 大
はじめに
前回の研究員の眼で、今後何回かに分けて、これまで慣れ親しんできた数学で使用されている記号の由来について、報告していくこととすると述べた1。
第1回目は、四則演算の記号(+、-、×、÷)の由来について、報告したが、第2回目の今回は、数字の関係を表す記号(=、≒、<、>等)について報告する。なお、今回報告する関係性を表す記号については、例えば幾何学や論理学においては異なる意味合いで使用されているものも多いが、ここでは代数学の記号としての意味合いを中心に説明しており、それ以外の意味合いについては必要に応じて補足的に説明しており、網羅的にカバーしているものではないことを述べておく。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications Inc.)
第1回目は、四則演算の記号(+、-、×、÷)の由来について、報告したが、第2回目の今回は、数字の関係を表す記号(=、≒、<、>等)について報告する。なお、今回報告する関係性を表す記号については、例えば幾何学や論理学においては異なる意味合いで使用されているものも多いが、ここでは代数学の記号としての意味合いを中心に説明しており、それ以外の意味合いについては必要に応じて補足的に説明しており、網羅的にカバーしているものではないことを述べておく。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications Inc.)
「=」(等号)の記号の由来
「=」(等号)記号は、現代においては幅広く使用され、国際的に認知されている記号である。
この記号を最初に使用したのは、ウェールズの数学者であるロバート・レコード(Robert Recorde)であると言われている。彼が、1557年にその著書「知恵の砥石(The Whetstone of Witte)」において、「…に等しい」という言葉を何度も使うことを避けるために、平行線を使った、とされている。これは、2本の平行線ほど等しいものは存在しない、という理由によるとされている。ただし、ロバート・レコードが使用した記号における平行線は、現在の「=」よりもずっと長いものであったようだ。
ただし、この記号は、当時はあまり広く使用されることはなかったようである。
当時の等号記号としては「=」はメジャーではなく、「‖」や「æ」、「œ」が使用されていたようだ。
そもそも、以前の印刷本では、「同等」を表すためには、通常aequales、aequantur、esgale、faciunt、 ghelijck、gleichといった用語が使用されていた。例えば、パスカルやフェルマーといった有名な数学者達は、equalのラテン語であるaequalcsやその略語であるaeqを使用していた。
さらに、ルネ・デカルト(René Descartes)は、aeqを2文字のaeとして、それを続けて無限大∞に類似した「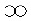 」というような記号を使用していたようである。
」というような記号を使用していたようである。
また、「代数学の父」とも呼ばれるローマ帝国時代のエジプトの数学者であるディオファントス(Diophantus of Alexandria)の著書「算術」(Arithmetica)が16世紀以降に翻訳された時には、「‖」の記号が使用されていた。
それが、「=」を、イングランドの数学者であるジョン・ウォリス(John Wallis)やアイザック・ニュートン(Sir Isaac Newton)等が使用することで、次第にその使用が広まっていき、ドイツの数学者であるゴットフリート・ライプニッツ(Gottfried Wilhelm Leibniz)が使用するようになって統一されていったとのことである。
なお、3本の平行線を用いた「≡」という記号もあるが、これは常に等号が成り立つ恒等式を方程式と明確に区別したいときに用いられる。具体的には、以下の通りである。
2x+3=5
2x+3≡3+2x (もちろん、「=」も使用される)
この「≡」記号は、図形の合同等を示す場合にも使用され、状況に応じて「恒等」、「同値」、「常に等しい」、「合同」等と呼ばれる。
この記号を最初に使用したのは、ウェールズの数学者であるロバート・レコード(Robert Recorde)であると言われている。彼が、1557年にその著書「知恵の砥石(The Whetstone of Witte)」において、「…に等しい」という言葉を何度も使うことを避けるために、平行線を使った、とされている。これは、2本の平行線ほど等しいものは存在しない、という理由によるとされている。ただし、ロバート・レコードが使用した記号における平行線は、現在の「=」よりもずっと長いものであったようだ。
ただし、この記号は、当時はあまり広く使用されることはなかったようである。
当時の等号記号としては「=」はメジャーではなく、「‖」や「æ」、「œ」が使用されていたようだ。
そもそも、以前の印刷本では、「同等」を表すためには、通常aequales、aequantur、esgale、faciunt、 ghelijck、gleichといった用語が使用されていた。例えば、パスカルやフェルマーといった有名な数学者達は、equalのラテン語であるaequalcsやその略語であるaeqを使用していた。
さらに、ルネ・デカルト(René Descartes)は、aeqを2文字のaeとして、それを続けて無限大∞に類似した「
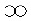 」というような記号を使用していたようである。
」というような記号を使用していたようである。また、「代数学の父」とも呼ばれるローマ帝国時代のエジプトの数学者であるディオファントス(Diophantus of Alexandria)の著書「算術」(Arithmetica)が16世紀以降に翻訳された時には、「‖」の記号が使用されていた。
それが、「=」を、イングランドの数学者であるジョン・ウォリス(John Wallis)やアイザック・ニュートン(Sir Isaac Newton)等が使用することで、次第にその使用が広まっていき、ドイツの数学者であるゴットフリート・ライプニッツ(Gottfried Wilhelm Leibniz)が使用するようになって統一されていったとのことである。
なお、3本の平行線を用いた「≡」という記号もあるが、これは常に等号が成り立つ恒等式を方程式と明確に区別したいときに用いられる。具体的には、以下の通りである。
2x+3=5
2x+3≡3+2x (もちろん、「=」も使用される)
この「≡」記号は、図形の合同等を示す場合にも使用され、状況に応じて「恒等」、「同値」、「常に等しい」、「合同」等と呼ばれる。
「≒」(ほぼ等しい)記号の由来
「≒」の記号は、ほとんど等しい、ほぼ等しい、あるいは近似的に等しい、というような意味合いで使用される。この記号の読み方は「ニアリーイコール(nearly equal)」となる。
例えば、円周率πについて、以下のように表現される。
π≒3.14
このように、「ニアリーイコール(nearly equal)」の状況を表すために、日本では「≒」の記号が使用されるが、海外では例えば「≐」といった記号がより一般的に幅広く使用されているようである。例えば、Microsoft社のWordの記号一覧表では、「≐」の方が「≒」よりも先に現われるし、その他の数式ソフトでも「≐」の記号がより高い位置付けに置かれているようである。
さらに、「≈」、「≃」、「~」、「≅」といった記号も同様や類似の意味合いで使用されているようである。
これらの記号のうち、「≐」という記号の由来については、1875年にドイツ人のシュタインハウザーがその著書「代数学」で初めて使用したとされている。「≐」や「≒」の記号を用いたのは、「=」と「≠」の中間的な記号として、点を1つ又は2つ残したと言われている。
いずれにしても、「=」記号が1557年に初めて使用されてから、300年以上とかなりの年月が経っており、その間に「=」の記号が定着するのに時間を要していたとしても、この期間の長さには若干の驚きを感じられるのではないか。
例えば、円周率πについて、以下のように表現される。
π≒3.14
このように、「ニアリーイコール(nearly equal)」の状況を表すために、日本では「≒」の記号が使用されるが、海外では例えば「≐」といった記号がより一般的に幅広く使用されているようである。例えば、Microsoft社のWordの記号一覧表では、「≐」の方が「≒」よりも先に現われるし、その他の数式ソフトでも「≐」の記号がより高い位置付けに置かれているようである。
さらに、「≈」、「≃」、「~」、「≅」といった記号も同様や類似の意味合いで使用されているようである。
これらの記号のうち、「≐」という記号の由来については、1875年にドイツ人のシュタインハウザーがその著書「代数学」で初めて使用したとされている。「≐」や「≒」の記号を用いたのは、「=」と「≠」の中間的な記号として、点を1つ又は2つ残したと言われている。
いずれにしても、「=」記号が1557年に初めて使用されてから、300年以上とかなりの年月が経っており、その間に「=」の記号が定着するのに時間を要していたとしても、この期間の長さには若干の驚きを感じられるのではないか。
(参考)近似を表す記号について
近似を表す記号については、「近似」が何を意味しており、どの分野で使用されているのか、さらには使用する個人によっても、その意味合いが異なってくることにもなる。
その意味では、上記で掲げた「~」、「≅」、「≈」、「≃」といった記号は、論理学や幾何学においては、「同値」、「同型」、「同相」、「漸進的に等しい」、「ホモトープである」といった意味合いを有することになる。
また、「≒」の上下の点の位置を逆にした「≓」という記号は、「≒」と同じく「ほとんど等しい」という意味合いで、上下の点の位置を真中に揃えた「≑」という記号は、「幾何学的に等しい」という意味合いで使用される。
その意味では、上記で掲げた「~」、「≅」、「≈」、「≃」といった記号は、論理学や幾何学においては、「同値」、「同型」、「同相」、「漸進的に等しい」、「ホモトープである」といった意味合いを有することになる。
また、「≒」の上下の点の位置を逆にした「≓」という記号は、「≒」と同じく「ほとんど等しい」という意味合いで、上下の点の位置を真中に揃えた「≑」という記号は、「幾何学的に等しい」という意味合いで使用される。
「<」、「>」、「≦」、「≧」(不等号)記号の使用と由来
「<」、「>」、「≦」、「≧」は、一括して不等号(前の2つが「単純不等号」、後の2つが「等号付不等号」)と呼ばれるが、それぞれの記号は「小なり」、「大なり」、「小なりイコール」、「大なりイコール」と呼ばれる。その他にも、「より小さい」、「より大きい」、「より小さいか又は等しい」、「より大きいか又は等しい」というような呼び方もされる。さらには、英語を用いて、「レスザン(less than)」、「グレイターザン(greater than)」、「レスザンオアイコール(less than or equal)」、「グレイターザンオアイコール(greater than or equal)」と呼ばれる。なお、後の2つについては「以上」、「以下」というような読み方もされる。
「<」、「>」の記号は、英国の数学者であるトーマス・ハリオット(Thomas Harriot)が、彼の死後の1631年に発表された「演習解析術(Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas (The Analytical Arts Applied to Solving Algebraic Equations))」の中で、初めて使用したと言われている。トーマス・ハリオットは、探検家のウォルター・ローリー((Sir Walter Raleigh)と親しく、北米を調査している時に、腕に のシンボルを有する原住民と出会って、このシンボルから2つの不等号が考案されたのではないかとの説があるようだ。
のシンボルを有する原住民と出会って、このシンボルから2つの不等号が考案されたのではないかとの説があるようだ。
なお、それ以前においては、多くの数学者達がそれぞれの不等号記号を考案してきており、例えば前回の研究員の眼「数学記号の由来について(1)-四則演算の記号(+、-、×、÷)-」において、「×」の記号を最初に使用したとして紹介したウイリアム・オートレッド(William Oughtred)は、「<」に対応するものとして「 」を、「>」に対応するものとして「
」を、「>」に対応するものとして「 」という記号を使用していたようである。
」という記号を使用していたようである。
一方で、「≦」、「≧」の記号については、フランスの数学者、天文学者であり、造船工学の先駆者として有名なピエール・ブーゲ(Pierre Bouguer)が1734年に使用したとされている。それ以前に、ジョン・ウォリスが1670年に、「-」が「<」の(現在の記号のような)下ではなく、上にある記号を用いたが、普及しなかったようである。
なお、日本においては、「<」や「>」の下に2本線の「=」を付した「≦」や「≧」といった記号を学ぶことになるが、欧米では1本線のみの「≤」「≥」や、不等号の下に平行な線を書いた「⩽」「⩾」と書く場合が多い。日本でも大学等では「≤」や「≥」がよく使用されてきている。
さらには、「=」でないことを強調するために、「≨」や「≩」といった記号が使用されることもある。
「<」、「>」の記号は、英国の数学者であるトーマス・ハリオット(Thomas Harriot)が、彼の死後の1631年に発表された「演習解析術(Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas (The Analytical Arts Applied to Solving Algebraic Equations))」の中で、初めて使用したと言われている。トーマス・ハリオットは、探検家のウォルター・ローリー((Sir Walter Raleigh)と親しく、北米を調査している時に、腕に
 のシンボルを有する原住民と出会って、このシンボルから2つの不等号が考案されたのではないかとの説があるようだ。
のシンボルを有する原住民と出会って、このシンボルから2つの不等号が考案されたのではないかとの説があるようだ。なお、それ以前においては、多くの数学者達がそれぞれの不等号記号を考案してきており、例えば前回の研究員の眼「数学記号の由来について(1)-四則演算の記号(+、-、×、÷)-」において、「×」の記号を最初に使用したとして紹介したウイリアム・オートレッド(William Oughtred)は、「<」に対応するものとして「
 」を、「>」に対応するものとして「
」を、「>」に対応するものとして「 」という記号を使用していたようである。
」という記号を使用していたようである。一方で、「≦」、「≧」の記号については、フランスの数学者、天文学者であり、造船工学の先駆者として有名なピエール・ブーゲ(Pierre Bouguer)が1734年に使用したとされている。それ以前に、ジョン・ウォリスが1670年に、「-」が「<」の(現在の記号のような)下ではなく、上にある記号を用いたが、普及しなかったようである。
なお、日本においては、「<」や「>」の下に2本線の「=」を付した「≦」や「≧」といった記号を学ぶことになるが、欧米では1本線のみの「≤」「≥」や、不等号の下に平行な線を書いた「⩽」「⩾」と書く場合が多い。日本でも大学等では「≤」や「≥」がよく使用されてきている。
さらには、「=」でないことを強調するために、「≨」や「≩」といった記号が使用されることもある。
「≠」、「⊀」、「⊁」記号の使用と由来
「≠」は、否定等号又は等号否定を表す記号で「ノットイコール」と呼ばれている。あくまでも「イコールではない」ことを示す。
同様に、「⊀」や「⊁」は、「より小さくない」、「より大きくない」ということを示している。
これらの否定記号では、元の記号に対して、否定の意味で「/(スラッシュ)」が付け加えられることになる。「/(スラッシュ)」が使用されるのは、タイプライターで重ね打ちするときに表しやすいということも関係していたようだ。
このように、「元の記号を否定する形で、別の記号を元の記号に付け加える方式」は、(現在使われている記号ではないが)レオンハルト・オイラー(Leonhard Euler)が採用していた。オイラーはクリスティアン・ゴールドバッハ(Christian Goldbach)に当てた手紙の中で、等しくないという意味合いで、「=」記号をベースにして、「 」という記号を使用していた。
」という記号を使用していた。
(参考)類似の記号
「≪」「≫」は、両者の比が極度に大きいことを示すために使用され、基本的には両方が正の数のときに使用される。「より非常に小さい」、「より非常に大きい」と呼ばれる。なお、「極度に大きい」ことの絶対的な基準はない。
同様に、「⊀」や「⊁」は、「より小さくない」、「より大きくない」ということを示している。
これらの否定記号では、元の記号に対して、否定の意味で「/(スラッシュ)」が付け加えられることになる。「/(スラッシュ)」が使用されるのは、タイプライターで重ね打ちするときに表しやすいということも関係していたようだ。
このように、「元の記号を否定する形で、別の記号を元の記号に付け加える方式」は、(現在使われている記号ではないが)レオンハルト・オイラー(Leonhard Euler)が採用していた。オイラーはクリスティアン・ゴールドバッハ(Christian Goldbach)に当てた手紙の中で、等しくないという意味合いで、「=」記号をベースにして、「
 」という記号を使用していた。
」という記号を使用していた。(参考)類似の記号
「≪」「≫」は、両者の比が極度に大きいことを示すために使用され、基本的には両方が正の数のときに使用される。「より非常に小さい」、「より非常に大きい」と呼ばれる。なお、「極度に大きい」ことの絶対的な基準はない。
最後に
今回も我々が日常幅広く使用している数字の関係性を表す等号(=)や不等号(<、>)の由来について報告してきた。今からすれば、極めて自然に受け入れられているこれらの記号ではあるが、そこに至るまでには、過去の偉大な数学者達がいくつかのアイデアを提案していく中で、多くの人々の共感が得られていくプロセスを経て、現在の形に落ち着いてきている。
ただし、今回のレポートでも報告したように、我々が小・中学校等で学んで使用してきた記号の中には必ずしもグローバルには一般的とはいえないものもある。それぞれの専門分野をさらに深めていくことになる大学教育等では、より世界で幅広く使用されている記号が使用されていくことになるようである。
さらに、1つの数学記号が、使用されている分野や個人等によって、異なる意味合いを有する状況にもなっている。
数学記号というと、極めてベーシックなもので、使用法等が厳密に一義的に定義されているというイメージがあるかもしれないが、こうした点については、十分に認識しておく必要があるだろう。
ただし、今回のレポートでも報告したように、我々が小・中学校等で学んで使用してきた記号の中には必ずしもグローバルには一般的とはいえないものもある。それぞれの専門分野をさらに深めていくことになる大学教育等では、より世界で幅広く使用されている記号が使用されていくことになるようである。
さらに、1つの数学記号が、使用されている分野や個人等によって、異なる意味合いを有する状況にもなっている。
数学記号というと、極めてベーシックなもので、使用法等が厳密に一義的に定義されているというイメージがあるかもしれないが、こうした点については、十分に認識しておく必要があるだろう。
本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2019年10月04日「研究員の眼」)
このレポートの関連カテゴリ
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月17日
EUの金融システムのリスクと脆弱性(2025秋)-欧州の3つの金融監督当局の合同委員会報告書 -
2025年10月17日
日本における「老衰死」増加の背景 -
2025年10月17日
選択と責任──消費社会の二重構造(1)-欲望について考える(2) -
2025年10月17日
首都圏の中古マンション価格~隣接する行政区単位での価格差は?~ -
2025年10月17日
「SDGs疲れ」のその先へ-2015年9月国連採択から10年、2030年に向け問われる「実装力」
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【数学記号の由来について(2)-数字の関係を表す記号(=、≒、<、>等)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数学記号の由来について(2)-数字の関係を表す記号(=、≒、<、>等)-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




