- シンクタンクならニッセイ基礎研究所 >
- 数学記号の由来について(4)-論理記号(∀、∃、∴、∵等)-
コラム
2020年04月30日
文字サイズ
- 小
- 中
- 大
はじめに
何回かに分けて、これまで慣れ親しんできた数学で使用されている記号の由来について、報告している1。
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について報告した。今回は、数学あるいは論理学で使用される「論理記号」の由来等について報告する。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について報告した。今回は、数学あるいは論理学で使用される「論理記号」の由来等について報告する。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
「∀」(全称記号)の使用及び由来
学生時代の数学の授業等で「すべての」という言葉を表すものとして「∀」という記号を使用していたのを覚えておられる方もいるのではないか。「∀x;P(x)」2と書いて、「すべてのxについてP(x)が成り立つ」ということを意味することになる。社会人になってからも、論理学に関係する本等を読めば、最も基本的な記号であるので、目にされた方もおられると思われる。
この記号は、「全称記号」、英語で「universal quantifier」と呼ばれている。英語で「すべての」を意味する「All」の頭文字の「A」を反転させた形になっていることから、割と自然に受け入れられてきたのではないかと思われる。
ただし、当初からこの記号が使用され、幅広く受け入れられてきたわけではない。
英国の数学者、哲学者、論理学者であるバートランド・ラッセル(Bertrand Russell)とアルフレッド・ノース・ホワイトヘッド (Alfred North Whitehead)は、その著「Principia Mathematica」(1910-1913年)において、全称記号を「( )」によって表現している。すなわち「すべてのxについてP(x)が成り立つ」ことを、「(x)P(x)」と表記した。この「( )」という記号は、「全ての」を意味するラテン語「omnis」の頭文字「O」に由来して、これを半分に割ったものだということである。この記号は、一定の影響力をもって使用された。
「∀」という記号を最初に使用したのは、ドイツの数学者、論理学者であるゲルハルト・ゲンツェン(Gerhard Gentzen)であると言われている。ゲンツェンが1935年に発表した論文「論理的推論についての研究(Untersuchungen ueber das logische Schliessen)」では、「All-Zeichen」(「全て記号」)として「∀」が使用された。この記号は、まさにドイツ語でも「すべての」を意味する「All」の頭文字「A」を反転させたものに由来している、とのことである。
ゲンツェンは、「( )」を採用しなかった理由として、「( )」が既に使われている括弧と区別が付きにくく混同を避けたかったため、だと説明している。
その他にも、「Π」や「∩」といった記号が全称記号として用いられることもあったが、「∀」という記号がその後の数理論理学を代表する教科書で採用されていったこと等もあり、幅広く定着していったようである。
2 因みに「;」は、数学や論理学では「such that」を意味している。
この記号は、「全称記号」、英語で「universal quantifier」と呼ばれている。英語で「すべての」を意味する「All」の頭文字の「A」を反転させた形になっていることから、割と自然に受け入れられてきたのではないかと思われる。
ただし、当初からこの記号が使用され、幅広く受け入れられてきたわけではない。
英国の数学者、哲学者、論理学者であるバートランド・ラッセル(Bertrand Russell)とアルフレッド・ノース・ホワイトヘッド (Alfred North Whitehead)は、その著「Principia Mathematica」(1910-1913年)において、全称記号を「( )」によって表現している。すなわち「すべてのxについてP(x)が成り立つ」ことを、「(x)P(x)」と表記した。この「( )」という記号は、「全ての」を意味するラテン語「omnis」の頭文字「O」に由来して、これを半分に割ったものだということである。この記号は、一定の影響力をもって使用された。
「∀」という記号を最初に使用したのは、ドイツの数学者、論理学者であるゲルハルト・ゲンツェン(Gerhard Gentzen)であると言われている。ゲンツェンが1935年に発表した論文「論理的推論についての研究(Untersuchungen ueber das logische Schliessen)」では、「All-Zeichen」(「全て記号」)として「∀」が使用された。この記号は、まさにドイツ語でも「すべての」を意味する「All」の頭文字「A」を反転させたものに由来している、とのことである。
ゲンツェンは、「( )」を採用しなかった理由として、「( )」が既に使われている括弧と区別が付きにくく混同を避けたかったため、だと説明している。
その他にも、「Π」や「∩」といった記号が全称記号として用いられることもあったが、「∀」という記号がその後の数理論理学を代表する教科書で採用されていったこと等もあり、幅広く定着していったようである。
2 因みに「;」は、数学や論理学では「such that」を意味している。
「∃」(存在記号)の使用及び由来
一方で、「∃」という記号は、「存在記号」、英語で「existential quantifier」と呼ばれている。「∃x;P(x)」と書いて、「P(x)が成り立つxが(少なくとも1つは)存在する」ということを意味することになる。
この記号についても、先のラッセルとホワイトヘッドの著「Principia Mathematica」の中では、「P(x)が成り立つxが存在する」ことを、「(E(x))P(x)」と表記している。
これに対して、ゲンツェンは、Eと言う文字が他にも(確率の期待値等)使用されていることから、「∀」と類似の考え方から、存在を意味するドイツ語の「Existieren」の頭文字のE(これは、存在を意味する英語の「Exist」の頭文字でもある)を反転させて、「∃」の記号を使うようになった、とのことである。
(参考)エプシロン・デルタ論法(ε-δ論法)
学生時代の数学でしばしば出てくるのが「ε-δ論法」であるが、この中で「∀」と「∃」の記号がよく使われることになる。すなわち、f1及びf2をxの関数とした場合
∀ε ∃δ; f1(x)<δ ⇒ f2(x) <ε
等と表現される。
より具体的には、例えば、「関数fが実数aにおいて連続であるとは、
∀ε ∃δ; |x―a|<δ ⇒ | f(x)-f(a)| <ε
と定義される、ことになる。
この記号についても、先のラッセルとホワイトヘッドの著「Principia Mathematica」の中では、「P(x)が成り立つxが存在する」ことを、「(E(x))P(x)」と表記している。
これに対して、ゲンツェンは、Eと言う文字が他にも(確率の期待値等)使用されていることから、「∀」と類似の考え方から、存在を意味するドイツ語の「Existieren」の頭文字のE(これは、存在を意味する英語の「Exist」の頭文字でもある)を反転させて、「∃」の記号を使うようになった、とのことである。
(参考)エプシロン・デルタ論法(ε-δ論法)
学生時代の数学でしばしば出てくるのが「ε-δ論法」であるが、この中で「∀」と「∃」の記号がよく使われることになる。すなわち、f1及びf2をxの関数とした場合
∀ε ∃δ; f1(x)<δ ⇒ f2(x) <ε
等と表現される。
より具体的には、例えば、「関数fが実数aにおいて連続であるとは、
∀ε ∃δ; |x―a|<δ ⇒ | f(x)-f(a)| <ε
と定義される、ことになる。
「∴」(ゆえに)、「∵」(なぜならば)記号の使用と由来
「∴」は、「ゆえに」あるいは「したがって」、英語では「therefore」と読まれ、それまでの議論の展開等から得られる結論を述べるために使われる。
以下のように3段論法などで使用されることになる。
A⇒B、B⇒C ∴A⇒C
一方で、「∵」は「なぜならば」あるいは「しかるに」、英語では「because」と読まれ、結論がそれ以前の議論等から得られる場合に、根拠を説明するために、使用される。
これらの記号は大変使い勝手が良い記号だと思われる。学生時代、問題を解いていて、最後の段階で、「∴」という記号を用いると、何となく「問題の証明を完了した」ということで、何とも言えない達成感や安堵感(?)に浸った経験はないだろうか。
これらの2つの記号については、割り算の記号「÷」や掛け算の記号「*」を最初に使用したということで、研究員の眼「数学記号の由来について(1)-四則演算の記号(+、-、×、÷)-」(2019.9.2)で紹介した数学者のヨハン・ハインリッヒ・ラーン(Johann Heinrich Rahn)が、1659年にその著書「Teutsche Algebra」で使用したのが最初と言われている。
ただし、この著書の中では、「∴」と「∵」はともに「ゆえに」の意味で使用されており、「∴」が主として使用されていた。ところが、この著書の1668年の英語翻訳版では、「∵」が主として使用されていた。いずれにしても18世紀の間は、「∴」と「∵」はともに同じような頻度で「ゆえに」の意味で使用されていた。
「∵」が「なぜならば」の意味で使用されるようになったのは19世紀に入ってからの英国や米国においてである。それは、1805年の「Gnetleman’s Mathematical Companion」の中で使用されたが、「ゆえに」の意味での「∴」ほどには、広く受け入れられなかったようである。その後1827年のケンブリッジ大学のメンバーによって編集された「Elements of Euclid」において、「∴」と「∵」がそれぞれの意味で使用されていたようである。
以下のように3段論法などで使用されることになる。
A⇒B、B⇒C ∴A⇒C
一方で、「∵」は「なぜならば」あるいは「しかるに」、英語では「because」と読まれ、結論がそれ以前の議論等から得られる場合に、根拠を説明するために、使用される。
これらの記号は大変使い勝手が良い記号だと思われる。学生時代、問題を解いていて、最後の段階で、「∴」という記号を用いると、何となく「問題の証明を完了した」ということで、何とも言えない達成感や安堵感(?)に浸った経験はないだろうか。
これらの2つの記号については、割り算の記号「÷」や掛け算の記号「*」を最初に使用したということで、研究員の眼「数学記号の由来について(1)-四則演算の記号(+、-、×、÷)-」(2019.9.2)で紹介した数学者のヨハン・ハインリッヒ・ラーン(Johann Heinrich Rahn)が、1659年にその著書「Teutsche Algebra」で使用したのが最初と言われている。
ただし、この著書の中では、「∴」と「∵」はともに「ゆえに」の意味で使用されており、「∴」が主として使用されていた。ところが、この著書の1668年の英語翻訳版では、「∵」が主として使用されていた。いずれにしても18世紀の間は、「∴」と「∵」はともに同じような頻度で「ゆえに」の意味で使用されていた。
「∵」が「なぜならば」の意味で使用されるようになったのは19世紀に入ってからの英国や米国においてである。それは、1805年の「Gnetleman’s Mathematical Companion」の中で使用されたが、「ゆえに」の意味での「∴」ほどには、広く受け入れられなかったようである。その後1827年のケンブリッジ大学のメンバーによって編集された「Elements of Euclid」において、「∴」と「∵」がそれぞれの意味で使用されていたようである。
「∨」(論理和)及び「∧」(論理積)記号の使用と由来
「∨」は、論理和(logical disjunction)記号で、「または」と読まれ、「A∨B」は「AまたはBのいずれか(または両方)が真であるときに真となる」ことになる。
「∧」は、論理積(logical conjunction)記号で、「かつ」と読まれ、「A∧B」は「AとBがともに真であるときのみ真となる」ことになる。
「∨」記号については、バートランド・ラッセルが1900年代にその原稿や論文等の中で使用した。
「∧」記号については、1930年にオランダの数学者、論理学者であるアレン・ハイティング(Arend Heyting)による「Die formalen Regeln der intuitionistischen Logik(直観主義的論理の公式ルール)」において、最初に使用されたとのことである。
「∧」は、論理積(logical conjunction)記号で、「かつ」と読まれ、「A∧B」は「AとBがともに真であるときのみ真となる」ことになる。
「∨」記号については、バートランド・ラッセルが1900年代にその原稿や論文等の中で使用した。
「∧」記号については、1930年にオランダの数学者、論理学者であるアレン・ハイティング(Arend Heyting)による「Die formalen Regeln der intuitionistischen Logik(直観主義的論理の公式ルール)」において、最初に使用されたとのことである。
その他の論理関係の記号の使用と由来について
「⇒」
「⇒」は、「ならば」と呼ばれ、含意を示しており、「A⇒B」は、「Aが真ならばBも真である」ことを意味している。「→」の記号を用いることもある。
「→」の記号は、1922年にデービッド・ヒルベルトによって最初に使用され、二重矢の「⇒」は、1954年にニコライ・ブルバキによって最初に使用された。
「¬」
「¬」は否定を表し、「¬A」は「Aが真ではない、偽である」ことを意味している。
この記号は、先のアレン・ハイティングの著書の中で最初に使用された。それ以前は、否定の意味を表すのに「~」(チルド)記号が使用されており、これはペアノによって1897年に使用された。
「⇔」、「≡」、「iff」
「⇔」、「≡」、「iff」は「同値」を意味しており、「A⇔B」は、「AとBの真偽関係が必ず一致する」ことを意味している。「iff」は、「if and only if」の略である。
「⇔」は、1954年にニコライ・ブルバキによって最初に使用された。
「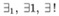 」
」
これらの記号は、「一意的に存在」していることを示しており、「∃1x;P(x)」と書いて、「P(x)が成り立つxが唯一存在する」ということを意味することになる。英語では「uniquness quantifier」と呼ばれている。
「⇒」は、「ならば」と呼ばれ、含意を示しており、「A⇒B」は、「Aが真ならばBも真である」ことを意味している。「→」の記号を用いることもある。
「→」の記号は、1922年にデービッド・ヒルベルトによって最初に使用され、二重矢の「⇒」は、1954年にニコライ・ブルバキによって最初に使用された。
「¬」
「¬」は否定を表し、「¬A」は「Aが真ではない、偽である」ことを意味している。
この記号は、先のアレン・ハイティングの著書の中で最初に使用された。それ以前は、否定の意味を表すのに「~」(チルド)記号が使用されており、これはペアノによって1897年に使用された。
「⇔」、「≡」、「iff」
「⇔」、「≡」、「iff」は「同値」を意味しており、「A⇔B」は、「AとBの真偽関係が必ず一致する」ことを意味している。「iff」は、「if and only if」の略である。
「⇔」は、1954年にニコライ・ブルバキによって最初に使用された。
「
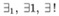 」
」これらの記号は、「一意的に存在」していることを示しており、「∃1x;P(x)」と書いて、「P(x)が成り立つxが唯一存在する」ということを意味することになる。英語では「uniquness quantifier」と呼ばれている。
最後に
今回は、数学あるいは論理学で使用される「論理記号」の由来等について報告してきた。
これらの記号も、我々が結構日常見かけることもあったのではないかと思われる。論理学を築き上げてきた大家たちがいろいろと頭を巡らせて、各種の記号を考案し、それらの中から、幅広く受け入れられたものが現代にまで残って普及してきていることになる。
これらについても、一筋縄ではいかずに、簡単に定まってきたわけではないことを改めて実感させられる。
これらの記号も、我々が結構日常見かけることもあったのではないかと思われる。論理学を築き上げてきた大家たちがいろいろと頭を巡らせて、各種の記号を考案し、それらの中から、幅広く受け入れられたものが現代にまで残って普及してきていることになる。
これらについても、一筋縄ではいかずに、簡単に定まってきたわけではないことを改めて実感させられる。
(2020年04月30日「研究員の眼」)
このレポートの関連カテゴリ
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【数学記号の由来について(4)-論理記号(∀、∃、∴、∵等)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数学記号の由来について(4)-論理記号(∀、∃、∴、∵等)-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




