曲線にはどんな種類があって、どう社会に役立っているのか（その10）－螺旋と渦巻の種類

曲線にはどんな種類があって、どう社会に役立っているのか（その10）－螺旋と渦巻の種類－

このレポートの関連カテゴリ

双曲螺旋

「双曲螺旋（hyperbolic spiral）」は、中心からの距離とともにピッチ角⁵が増加する螺旋で、以下の極方程式で表される。

r=a／θ

因みに、直交座標表示では、以下のような算式となる。

この曲線は、無限遠点に発散し、ｙ＝a に漸近する（θが負の場合も含めると、ｙ軸に対して線対称になる）。

双曲螺旋は、螺旋階段を上る眺めに相当し、螺旋銀河や建築の渦巻きをモデル化するためにも使用される。また、陸上競技の200mと400mレースのスタートマークは、双曲螺旋に沿ってずらされた位置に配置される。これにより、同心円状のレーンに制限されたランナー全員が、フィニッシュラインまで同じ長さの経路を持つことが保証される⁶。

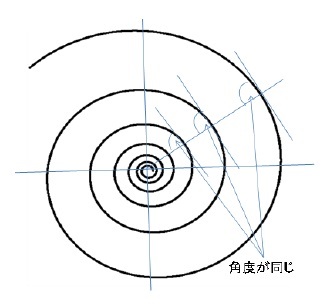
⁵ 螺旋の中心を中心として、その螺旋上の点の1つを通る円と螺旋（の接線）によって作成される角度。対数螺旋は、螺旋上の全ての点でピッチ角が不変のままであるという特性によって特徴付けらが、アルキメデスの螺旋では、角度は距離とともに減少し、双曲螺旋では、角度は距離とともに増加する。
⁶ 走者がスタート後に内側のレーンに移動する長距離レースでは、代わりに別の螺旋（円のインボリュート）が使用される。

リチュース（螺旋）

「リチュース（Lituus）」は、角度θが半径rの 2 乗に反比例する螺旋である。リチュースは、円形セクターの面積が一定のままになるように移動する点Pの軌跡となっている。名称の「リチュース」は、古代ローマの宗教でアウグル（司祭かつ役人）が空の儀式空間（テンプルム（templum））を示すためにカルト楽器として使用した曲がった杖（一部の西ヨーロッパのクロシエ（司教のスタッフ（職杖））の上部に形が似ている）であり、これに因んでいるようだ。

この螺旋は、以下の極方程式で表される。

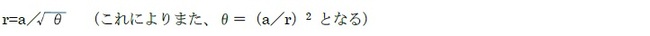
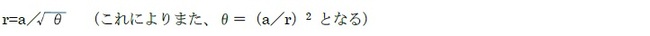
因みに、直交座標表示では、以下のような算式となる。

r の符号に応じて 2つの分岐を持ち、θが大きくなると、ｘ軸に漸近する。

対数螺旋

「対数螺旋（logarithmic spiral）」は、後に説明する特性から「等角螺旋（equiangular spiral）」、またその研究に貢献した17世紀のスイスの数学者ヤコブ・ベルヌーイ（Jakob Bernoulli）に因んで「ベルヌーイの螺旋（Bernoulli's spiral）」とも呼ばれる。特に黄金比φに関連するもの⁷を「黄金螺旋（golden spiral）」という。

対数螺旋については、これまでの研究員の眼でも紹介してきた。具体的には、研究員の眼「ネイピア数eについて（３）－実際の社会における自然現象等の表現において、どのように現れてくるのか－」（2018.5.22）において、ネイピア数eが現れる世界の例として取り上げた。また、研究員の眼「黄金比φについて（その２）－黄金比はどこで使用され、どんな場面で現れているのか－」（2020.11.20）では、自然界で見られる黄金比の紹介の中で「黄金螺旋」について紹介した。詳しくは、これらのコラムを参照していただくことにして、前者からの抜粋に基づくと、以下の通りとなっている。

対数螺旋は、極方程式では

r＝ae^b^θ　

と表される。ここに、e はネイピア数、a、b は実数である。

これを直交座標表示で表すと、以下の通りとなる。

ｘ＝ae^b^θcosθ　　ｙ＝　ae^b^θsinθ

rは原点からの距離を表す。

aは正値でスケールファクターとなっている。

bが螺旋の形状に大きな影響を与え、中心から離れる際に

(1) bが正値の場合は、左曲がりの螺旋になり、(2) bが負値の場合は、右曲がりの螺旋になる。

また、対数螺旋のどの点をとっても、その点と原点を結ぶ直線とその点における接線が交わる角度が一定になる。即ち、θが位置を表す角度を示しているが、交角はθによらない。このため、対数螺旋は「等角螺旋」と呼ばれる。

なお、対数螺旋は自己相似であり、任意の倍率で拡大又は縮小したものは、適当な回転によって元の螺旋と一致する。

⁷ 以下の極方程式において、｜b|=2logφ／π≈0.30634896253　の場合に相当している。

クロソイド（曲線）

「クロソイド（曲線）（clothoid（curve））」というのは、「曲率が曲線の長さに比例して線形に変化する曲線」である。この曲線が使用されている分野によって、「オイラー螺旋（Euler spiral）」や「コルヌ螺旋（Cornu spiral）」とも呼ばれている。

クロソイド曲線を算式で表すと、Rを曲率半径、Lをクロソイド曲線の長さ、Aをクロソイドパラメータとして、

R×L＝A2

となる（R、L、Aのうちの2つの要素が与えられれば、クロソイド曲線の形が決まる）。

クロソイドについては、以前の研究員の眼「曲線にはどんな種類があって、どう社会に役立っているのか（その４）－クロソイド曲線－」（2024.2.20）で紹介したので、これを参照していただきたい。

テオドロスの螺旋

「テオドロスの螺旋（Spiral of Theodorus）」は、連続した直角三角形で構成される曲線である。「平方根螺旋（square root spiral）」、「ピタゴラス螺旋（Pythagorean spiral）」又は「ピタゴラスのカタツムリ（Pythagoras's snail）」とも呼ばれる。紀元前5世紀の古代ギリシャの数学者であるキュレネ⁸のテオドロスに因んで名付けられている。

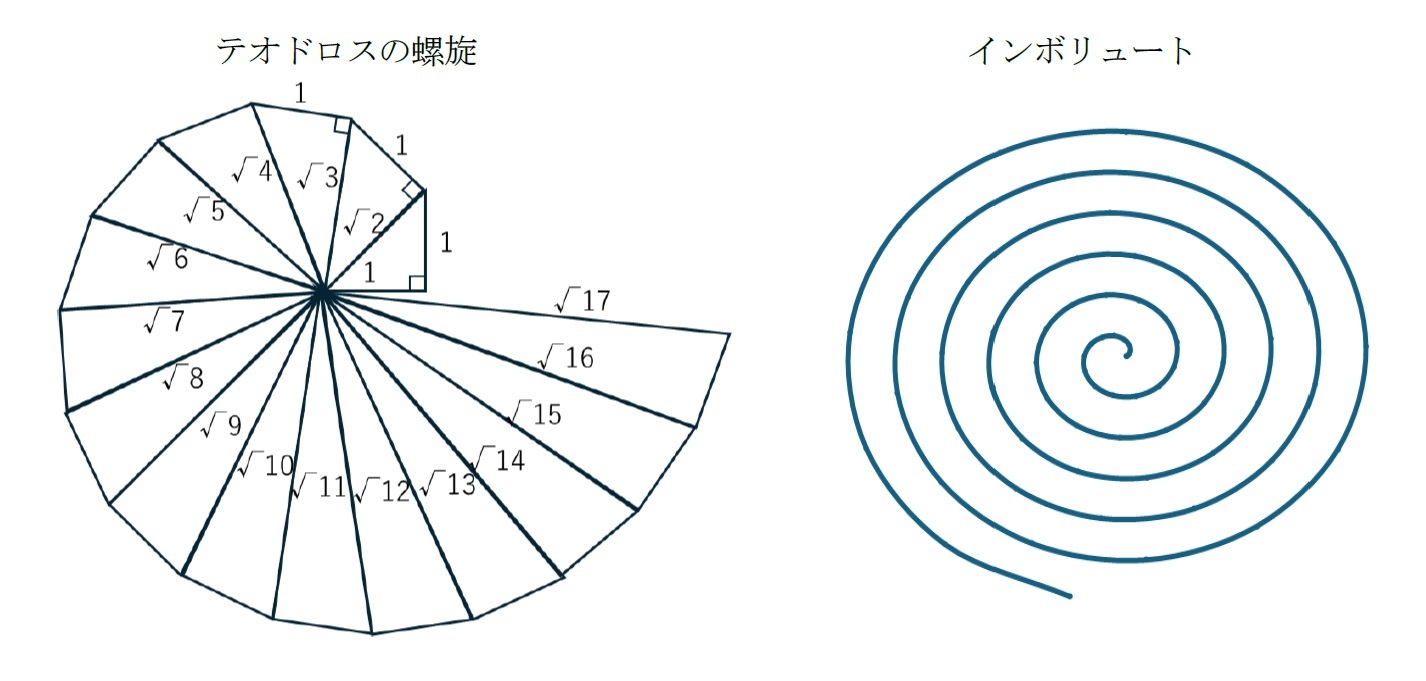
この螺旋は、以下の図が示すように、「長さ1の二等辺を有する直角三角形で始まり、その斜辺と直角に交わる辺の長さを1とする別の直角三角形を形成し、さらにその直角三角形の斜辺と直角に交わる辺の長さを1とする別の直角三角形を形成する」というプロセスを繰り返して形成される。斜辺の長さが　　　の直角三角形が他の図と重ならない最後の三角形となる。

なお、このプロセスを無限に繰り返していった場合でも、どの２つの斜辺も一致することはないことが証明されている。

テオドロスの螺旋は、アルキメデスの螺旋の近似曲線となっており、アルキメデスの螺旋の2つの巻きの間の距離がπに等しいのと同様に、テオドロスの螺旋の回転数が無限大に近づくにつれて、2つの連続する巻きの間の距離は急速にπに近づいていく。

⁸ 現在の北アフリカのリビア北東部にある当時の古代ギリシャの植民地であった都市

インボリュート（曲線）

「インボリュート（曲線）（involute (curve)）」は、その法線⁹が常に一つの定円に接するような曲線で、「伸開線」、「円の伸開線 （involute of circle）」あるいは「反クロソイド（anti-clothoid）」とも呼ばれる。固定されて回転しない円形のリールに巻き取られた糸を弛まないようにほどいていったときに、糸の先端（等の1点）が描く曲線が、インボリュート曲線となる。「in」は「内」、「volute」は「巻く」の意味があることから「内巻き線」ということになる¹⁰。

媒介変数表示では、以下のように表される。

ｘ＝a（cosθ＋θsinθ）
ｙ＝a（sinθ－θcosθ）

インボリュートは上記右の図形となり、アルキメデスの螺旋と形状は似ているが、同一ではない。

⁹ ある直線と垂直に交わる直線

¹⁰ これに対して「エボリュート（evolute）」は、「縮閉線」は、曲線の各点における曲率円の中心の軌跡となる。これはまた、曲線の法線の包絡線（与えられた曲線族と接線を共有する曲線）となる。

最後に

以上、今回は、「螺旋」や「渦巻」の主要な種類について、その数式での表現と特性等について、簡単に紹介してきた。

実は、今回紹介したもの以外にもさらなる別のタイプの渦巻も考えられると思われるが、あくまでも今回は、数学的にも意味合いが大きく、重要と思われるものを紹介させていただいた。

次回の研究員の眼では、日常生活の中で見ることができる「螺旋」や「渦巻」の例について紹介することとする。

日付	タイトル	執筆者	媒体
2025/03/18	EUがIRRD(保険再建・破綻処理指令)を最終化－業界団体は負担の軽減とルールの明確化等を要求－	中村亮一	基礎研レポート
2025/03/10	ドイツの民間医療保険及び民間医療保険会社の状況（２）－2023年結果－	中村亮一	保険・年金フォーカス
2025/03/03	ドイツの民間医療保険及び民間医療保険会社の状況（１）－2023年結果－	中村亮一	保険・年金フォーカス
2025/02/19	EIOPAがソルベンシーIIのレビューに関する助言のいくつかを提出－欧州委員会からの要請に対する回答－	中村亮一	保険・年金フォーカス

日付

タイトル

執筆者

媒体

2025/03/18

EUがIRRD(保険再建・破綻処理指令)を最終化－業界団体は負担の軽減とルールの明確化等を要求－

中村亮一

基礎研レポート

2025/03/10

ドイツの民間医療保険及び民間医療保険会社の状況（２）－2023年結果－

中村亮一

保険・年金フォーカス