曲線にはどんな種類があって、どう社会に役立っているのか（その７）－サイクロイド・トロコイド（その応用）

曲線にはどんな種類があって、どう社会に役立っているのか（その７）－サイクロイド・トロコイド（その応用）－

このレポートの関連カテゴリ

研究員の眼

はじめに

学生時代に、複雑な算式を図表で表すと、いろんな形の曲線が描かれるのを勉強したと思う。この時には、「へー、そうなんだ」ぐらいの認識でおられた方も多く、むしろ、こうした算式の取扱いに四苦八苦して、結果として得られている曲線が、社会において、あるいは自然界において、どのような形で現れていて、どう役立っているのか、については、あまり説明がなく、殆ど勉強する機会もなかったのではないかと思われる。

ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。これまでの4回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」、「カテナリー曲線」及び「クロソイド曲線」について報告した。

今回は、「サイクロイド曲線」等について、複数回に分けて報告している。過去の2回で「サイクロイド」、「トロコイド」、「リマソン」等の曲線について、それらがどのようなもので、どのように表現されているのかを紹介してきた。この研究員の眼では、これらのサイクロイド曲線等がどう社会に役立っているのかについて報告する。

サイクロイド歯車

「サイクロイド歯車（cycloid gear）」というのは、文字通り、サイクロイド曲線形状の歯を有する歯車である。殆どの歯車においては、「インボリュート歯車（involute gear）」という形式が使用されているが、機械式のクロック（置時計）やウォッチ（腕時計）、計器等の精密部品においては、サイクロイド歯車が使用されている。

「インボリュート歯車」というのは、まさにインボリュート曲線形状の歯を有する歯車のことである。ここでの「インボリュート曲線（involute curve）」というのは、その法線¹が常に一つの定円に接する平面曲線で、「円の伸開線（involute of circle）」又は「反クロソイド（anti-clothoid）」とも呼ばれる。固定されて回転しない円形のリールに巻き取られた糸を弛まないようにほどいていったときに、糸の先端（等の1点）が描く曲線が、インボリュート曲線となる。

サイクロイド歯車とインボリュート歯車の大まかなイメージは、以下の通りとなっている。インボリュート歯車の歯先と歯元は１つのインボリュート曲線で形成されているが、サイクロイド歯車の歯先はエピサイクロイド曲線、歯元はハイポサイクロイド曲線で形成されている。

インボリュート歯車のメリットとしては、二つの歯の接点における接線が共通するような形になっているため、歯車の回転速度が一定になり、歯車の間のエネルギー伝導が最適になることが望めることが挙げられている。また、形状がシンプルで加工が簡単、低価格であることから、多くの機器の歯車で使用されている。

これに対して、サイクロイド歯車のメリットは、インボリュート歯車に比べて、フラットに製造できることから、研磨が容易になることや、歯の接点が少ないので、摩擦と摩耗の両方が減少することが挙げられている。一方で、加工は難しくなる。

¹ 曲線上の一点において、その点での接線に垂直な直線。

遊星歯車機構

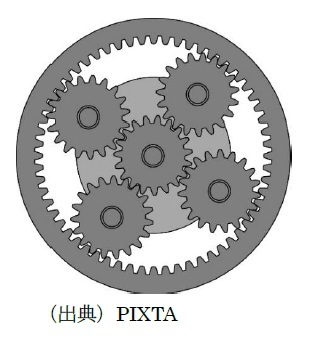「遊星歯車機構（epicyclic gear train 又はplanetary gearset）」は、太陽歯車（sun gear）の中心の周りを複数の遊星歯車（planetary gear）が自転しつつ公転する構造を有する歯車機構である。１つのユニットは、（右図が示しているように）太陽歯車、遊星歯車、遊星キャリア（planetary gear）及び外輪歯車（outer gear）で構成されている。

遊星キャリアは遊星歯車の中心をつなぎ、回転して、太陽歯車の周りに遊星歯車を運ぶ。遊星歯車と太陽歯車は噛み合い、ピッチ円²を滑らずに転がる。例えば、太陽歯車が固定されている場合、遊星歯車のピッチ円上の点はエピサイクロイド曲線をたどる。

太陽歯車の回転、遊星歯車の公転（キャリヤの回転）、外輪歯車の回転の3つの要素のそれぞれを固定・入力・出力に割り当てるかによって、一つのユニットで複数の減速比や回転方向の切替えが可能となる。

遊星歯車機構は、オートマチックトランスミッションの変速装置や自転車の内装型変速機、さらには多くの産業機械で使用されている。

² 歯車の中心から歯車同士が接触する点までの距離を半径とする円

サイクロイドドライブ

減速機は、駆動（入力）側の軸回転数を一定の比率で減速して、従動（出力）軸に取り出す装置であり、一般的な減速機はインボリュート歯形を有する平歯車を組み合わせているが、「サイクロイドドライブ（cycloidal drive）」又は「サイクロイド減速機（cycloidal speed reducer）」は、サイクロイド歯形を有するサイクロイドディスクを使用している。

サイクロイドドライブは、遊星歯車機構等のギアベースのトランスミッションよりも、そのサイズに比して接触面積が大きく設計でき、非常に高いトルク出力が得られる。サイクロイド減速機は、バックラッシュ³が非常に低く、コンパクトなサイズで比較的高い減速比率が可能となる。

サイクロイド減速機は、産業用ロボットや産業機器、ポンプや自動車などの駆動部分、船のスクリュー、航空機や風力発電のプロペラ部などに使用されている。

³ 部品間のギャップによって引き起こされるメカニズムのクリアランス又は動きの損失。

サイクロイド振り子

「サイクロイド振り子（cycloidal pendulum）」は、軌道がサイクロイド曲線に従う振り子である。

通常の単振り子は、周期が振幅に依存するが、サイクロイド振り子の場合、サイクロイドの等時性により、振幅によらずに周期が一定になる⁴。サイクロイド振り子は、この振り子を研究し、初めて実際に振り子時計を制作したクリスティアーン・ホイヘンス（Christiaan Huygens）⁵の名前に因んで「ホイヘンス振り子」と呼ばれることもある。

振り子を時計代わりに使用する場合、振幅は徐々に減衰していくので、その周期が振幅に依存するのは適当でない。サイクロイド振り子の周期Tは、振幅によらずに、ℓを振り子の長さ（このとき、サイクロイドの動円の半径はℓ／4となる）とすると、以下の通りとなる。

以下の図が示しているように、振り子の振幅が大きくなると、両端の曲線が障害物となって、実際の振幅が小さくなることで、（円弧軌道の場合に比べて）周期が短くなり、これによって周期が一定になる仕組みになっている。障害物となる両端の曲線はサイクロイド曲線であり、振り子の重りはそれと同じ大きさのサイクロイド曲線を描くようになっている⁶。

⁴ ガリレオ・ガリレイが振り子の等時性を発見したとされているが、彼の探求した単振り子（円弧の軌道を描く）では、振幅が小さい時には、近似的には（単振動と同じ運動とみなされ）等時性が成り立つが、振幅が大きくなると、周期が長くなってしまう。
⁵ 前々回の研究員の眼で紹介したように、ホイヘンスは「等時降下曲線がサイクロイド曲線である」ことを証明している。
⁶ ある曲線に対して、その曲率円の中心の軌跡を「エボリュート（Evolute）又は縮閉線」、その元の曲線を「インボリュート（Involute）又は伸開線」と呼んでいるが、縮閉線上のある1点を固定し、そこを起点にして、糸を縮閉線からほどいていくときに、その糸の先端が描く軌跡が伸開線になる。ここでは振り子の糸がまとわりつく障害物の曲線が縮閉線、糸がほどかれていくときに描かれる曲線が伸開線になっている。また、サイクロイドの伸開線と縮閉線は、ともに同じ大きさのサイクロイドとなる。なお、P1で述べたように、通常「インボリュート曲線」は円の伸開線を指している。

建造物

サイクロイドによるアーチは、正円によるアーチに比べて、横に広がりのあるフラットなアーチになっている。これは円弧の中心が複数ある多芯円で近似される。

米国の建築家ルイス・カーン（Louis I. Kahn）は、テキサス州フォートワースにある「キンベル美術館（Kimbell Art Museum）」の設計にサイクロイドアーチを使用している。ギャラリーのヴォールトに（正円に比べて）比較的平坦なサイクロイド曲線を使用することで、天井の高さが低くなり、高さに比して幅の広い優雅な回廊を生み出す形になっている。

その他の建造物でもサイクロイド曲線やそれに近似される曲線が使用される例が見られるようだ。

神社建築の屋根

古くからの神社仏閣は木造建築となっているが、そこでは雨が耐用年数を縮めてしまうことから、雨対策が重要になってくる。この１つとして、屋根に雨が落ちた場合に、最速で流れるように、その勾配においては「サイクロイド曲線」が使用されていたりする。

ヴァイオリンのボディの輪郭

ヴァイオリンのボディの輪郭は美しいアーチ形状を有しているが、実はこのデザインにもサイクロイドが関係しているようだ。

クレモナの巨匠がアーチのデザインを得るためにおそらく使っていただろうと現在幅広く認められているのが、カーテートサイクロイド（Curtate Cycloid）だと言われている。

日付	タイトル	執筆者	媒体
2025/03/18	EUがIRRD(保険再建・破綻処理指令)を最終化－業界団体は負担の軽減とルールの明確化等を要求－	中村亮一	基礎研レポート
2025/03/10	ドイツの民間医療保険及び民間医療保険会社の状況（２）－2023年結果－	中村亮一	保険・年金フォーカス
2025/03/03	ドイツの民間医療保険及び民間医療保険会社の状況（１）－2023年結果－	中村亮一	保険・年金フォーカス
2025/02/19	EIOPAがソルベンシーIIのレビューに関する助言のいくつかを提出－欧州委員会からの要請に対する回答－	中村亮一	保険・年金フォーカス

日付

タイトル

執筆者

媒体

2025/03/18

EUがIRRD(保険再建・破綻処理指令)を最終化－業界団体は負担の軽減とルールの明確化等を要求－

中村亮一

基礎研レポート

2025/03/10

ドイツの民間医療保険及び民間医療保険会社の状況（２）－2023年結果－

中村亮一

保険・年金フォーカス