- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 曲線にはどんな種類があって、どう社会に役立っているのか(その2)-円錐曲線(楕円、放物線、双曲線)が現れる場面-
コラム
2023年11月01日
文字サイズ
- 小
- 中
- 大
はじめに
今回の研究員の眼のシリーズでは、「曲線」(あるいは「曲面」)について、どんな種類があって、それらが実際の社会において、どのような場面で現れてきて、どう社会に役立っているのかについて、報告しようとしている。
まずは、前回は、楕円、放物線、双曲線等の「円錐曲線」について、その定義等について説明したが、今回はそれらが社会において現れてくる場面等について報告する。
なお、それぞれの冒頭において、円錐曲線の一般的な定義を繰り返しておく。
まずは、前回は、楕円、放物線、双曲線等の「円錐曲線」について、その定義等について説明したが、今回はそれらが社会において現れてくる場面等について報告する。
なお、それぞれの冒頭において、円錐曲線の一般的な定義を繰り返しておく。
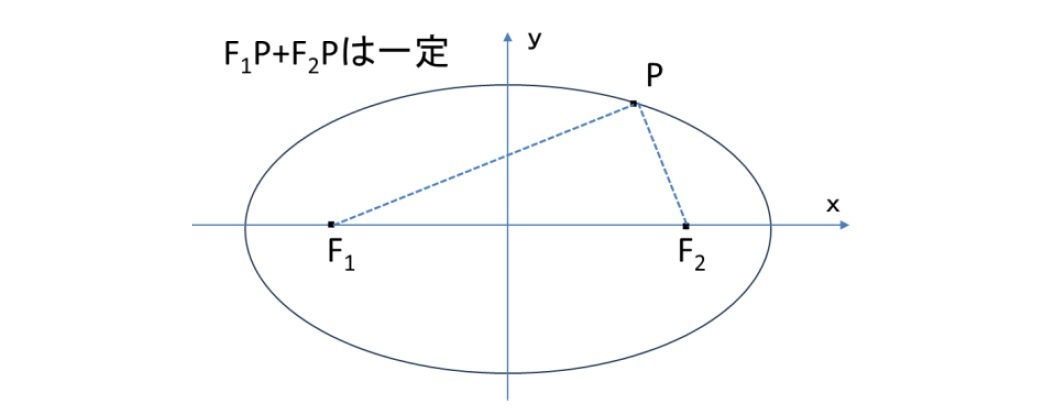
楕円
1 「離心率」の定義については、研究員の眼「曲線にはどんな種類があって、どう社会に役立っているのか(その1)-円錐曲線(楕円、放物線、双曲線)とは-」(2023.10.16)で説明している。
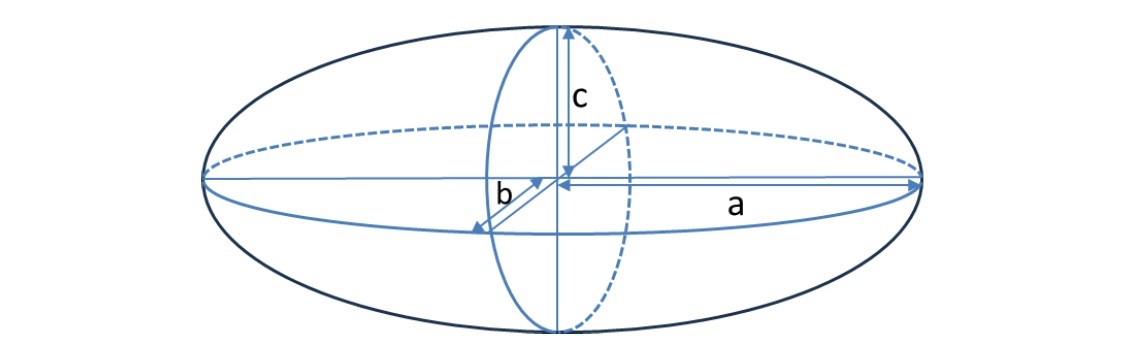
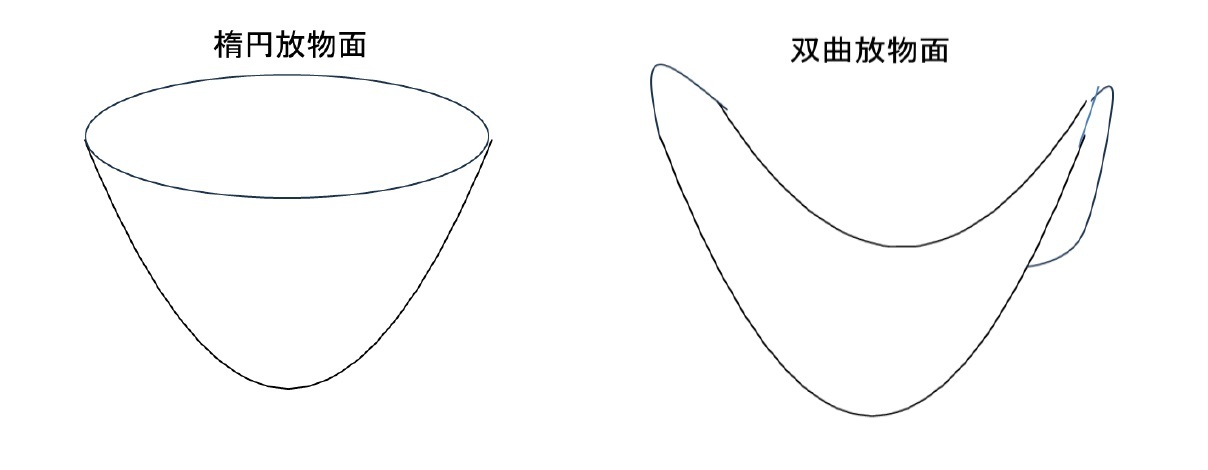
楕円体
また a, b, c のうちいずれか2つが等しい楕円体は、楕円の軸を中心に楕円を回転して得られる回転体となり、「回転楕円体(spheroid)」と呼ばれる。このうち、長軸を回転軸にしたもの(a=b<cとなるケース)を「長球(prolate)」(又は「長楕円体」等)、短軸を回転軸にしたもの(a=b>cとなるケース)を「扁球(oblate)」(又は「扁楕円体」)という。
楕円や楕円面が現れる場面(その1)
楕円が現れる場面として、最も有名なのは、惑星や衛星や人工衛星の軌道が「楕円軌道」を描くということだろう。
有名なドイツの天文学者ヨハネス・ケプラーによって発見された惑星の運動法則である「ケプラーの法則」が有名であるが、その第1法則が「楕円軌道の法則」で、惑星は太陽を焦点の一つとする楕円軌道を描く、というものである2。その意味するところは、太陽の位置は楕円の中心ではなく、あくまでも焦点の1つである、ということであり、もう片方の焦点には何もない。
もちろん、日常生活の中でも、楕円は多くの場面で観察される。具体的には、例えば、円形のお皿や時計盤等は真正面から見れば円形になるが、斜めから見れば楕円の形をしている。同様に、コップに入れた水を上から見た場合、テーブルに置かれた状態では円形だが、コップを斜めにすれば、水面は楕円形になる。さらには、ラグビーボールは楕円体となっている。
また、地球自体は、自転により赤道から外に向かって働く遠心力により、球体ではなく、楕円体となっている。
さらには、ホワイトハウスの米国大統領執務室は、その形から「オーバルオフィス」と呼ばれている。「オーバル(oval)」というのは、通常、卵型・長円あるいは楕円に似た曲線や、卵形・長円形・楕円形のことを指しているが、オーバルオフィスは楕円形となっている3。
2 因みに、第2法則は「面積速度一定の法則」と呼ばれ、「惑星と太陽を結ぶ線分が単位時間に描く面積(面積速度)は、一定である」というものである。これは、太陽に近いところでは惑星は速度を増し、太陽から遠いところでは惑星は速度を落とすことを意味している。また、第3法則は「調和の法則」と呼ばれ、「惑星の公転周期の2乗は、軌道長半径の3乗に比例する」というものである。これは、公転周期の長さは(離心率には依存せず)楕円軌道の長半径のみに依存して決まることを意味している。
3 なお、「楕円積分」、「楕円関数」、「楕円曲線」は、楕円の弧長に関係して研究されてきたものである。例えば「楕円曲線」は楕円形をした曲線を示しているわけではないが、フェルマーの最終定理の証明や楕円曲線暗号等といった暗号理論において使用され、重要な役割を果たしてきている。
有名なドイツの天文学者ヨハネス・ケプラーによって発見された惑星の運動法則である「ケプラーの法則」が有名であるが、その第1法則が「楕円軌道の法則」で、惑星は太陽を焦点の一つとする楕円軌道を描く、というものである2。その意味するところは、太陽の位置は楕円の中心ではなく、あくまでも焦点の1つである、ということであり、もう片方の焦点には何もない。
もちろん、日常生活の中でも、楕円は多くの場面で観察される。具体的には、例えば、円形のお皿や時計盤等は真正面から見れば円形になるが、斜めから見れば楕円の形をしている。同様に、コップに入れた水を上から見た場合、テーブルに置かれた状態では円形だが、コップを斜めにすれば、水面は楕円形になる。さらには、ラグビーボールは楕円体となっている。
また、地球自体は、自転により赤道から外に向かって働く遠心力により、球体ではなく、楕円体となっている。
さらには、ホワイトハウスの米国大統領執務室は、その形から「オーバルオフィス」と呼ばれている。「オーバル(oval)」というのは、通常、卵型・長円あるいは楕円に似た曲線や、卵形・長円形・楕円形のことを指しているが、オーバルオフィスは楕円形となっている3。
2 因みに、第2法則は「面積速度一定の法則」と呼ばれ、「惑星と太陽を結ぶ線分が単位時間に描く面積(面積速度)は、一定である」というものである。これは、太陽に近いところでは惑星は速度を増し、太陽から遠いところでは惑星は速度を落とすことを意味している。また、第3法則は「調和の法則」と呼ばれ、「惑星の公転周期の2乗は、軌道長半径の3乗に比例する」というものである。これは、公転周期の長さは(離心率には依存せず)楕円軌道の長半径のみに依存して決まることを意味している。
3 なお、「楕円積分」、「楕円関数」、「楕円曲線」は、楕円の弧長に関係して研究されてきたものである。例えば「楕円曲線」は楕円形をした曲線を示しているわけではないが、フェルマーの最終定理の証明や楕円曲線暗号等といった暗号理論において使用され、重要な役割を果たしてきている。
楕円や楕円面が現れる場面(その2)
楕円面には2つの焦点があるが、一方の焦点からでた光や音は、楕円面で反射して他方の焦点を通る。こうしてその光や音は再び楕円面で反射して元の焦点へ帰る、ということを限りなく繰り返すことになる。
この性質を利用するものとして、「電灯のグローブ」があり、これにより一つの点に多量の光が集中する光源になる。あるいは、ミステリー番組等でたまに紹介される仕組みとして、楕円面の天井をもった部屋では、一方の焦点に立って声を出せば、他方の焦点にいる人にだけ鮮明に伝えられる、という現象が起きることになる。米国の国会議事堂やロンドンのセントポール大聖堂の回廊で、この仕組みが確認できる。
この性質を利用するものとして、「電灯のグローブ」があり、これにより一つの点に多量の光が集中する光源になる。あるいは、ミステリー番組等でたまに紹介される仕組みとして、楕円面の天井をもった部屋では、一方の焦点に立って声を出せば、他方の焦点にいる人にだけ鮮明に伝えられる、という現象が起きることになる。米国の国会議事堂やロンドンのセントポール大聖堂の回廊で、この仕組みが確認できる。
放物線
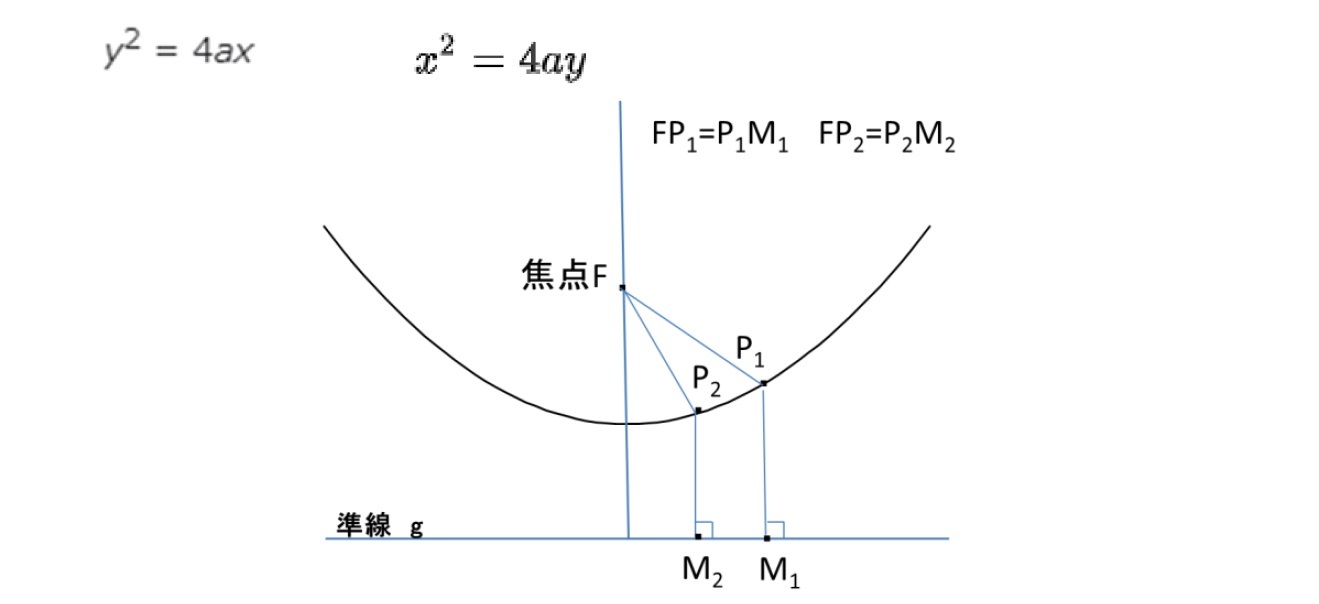
放物線は、二次曲線の一種で、離心率は 1 である。
・焦点が(0, c)、準線が y =-c のとき、放物線の式 x2 = 4cy となる。
・焦点が(c, 0)、準線が x =-c のとき、放物線の式は y2 = 4cx となる。
・二次関数 y = ax2 + bx + c (a は 0 ではない)が描くグラフは放物線になる。
4 放物線に類似の形をしていて、混同される曲線に、ロープや電線等を、両端を持って垂らしたときにできる「懸垂線(カテナリー曲線)」があるが、これについては、次回以降の研究員の眼で紹介する。
・焦点が(0, c)、準線が y =-c のとき、放物線の式 x2 = 4cy となる。
・焦点が(c, 0)、準線が x =-c のとき、放物線の式は y2 = 4cx となる。
・二次関数 y = ax2 + bx + c (a は 0 ではない)が描くグラフは放物線になる。
4 放物線に類似の形をしていて、混同される曲線に、ロープや電線等を、両端を持って垂らしたときにできる「懸垂線(カテナリー曲線)」があるが、これについては、次回以降の研究員の眼で紹介する。
放物線や放物面が現れる場面(その1)
放物線が現れる実用的な場面として、最も有名なのは、「パラボラアンテナ」(衛星放送のアンテナ)においてであろう。「パラボラアンテナ」は、放物線(パラボラ)をその軸に関して回転させたときにできる図形である回転放物面(パラボロイド)になっている。
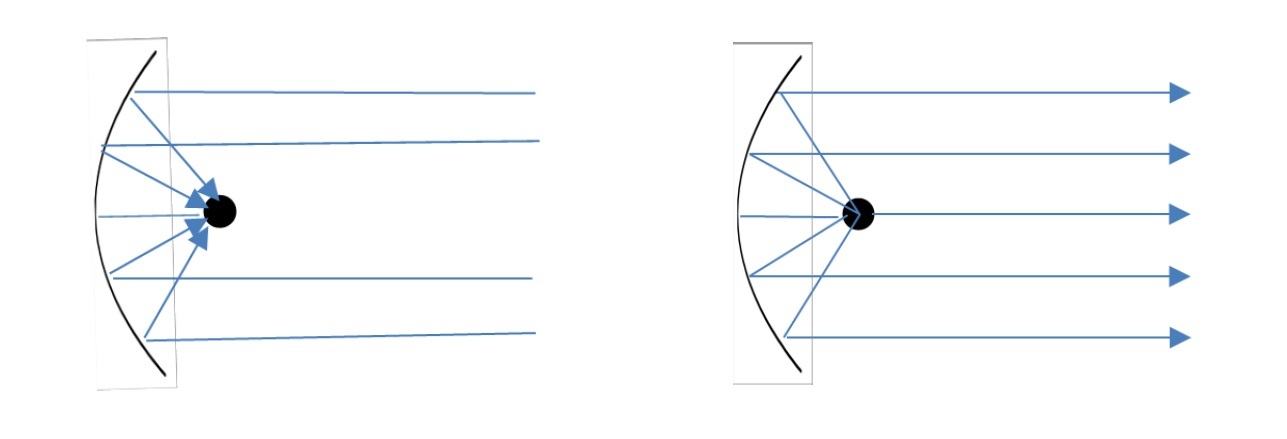
回転放物面に平行に入射した電磁波(光)や音は、放物線の焦点のただ一点に集まる(しかも、同時に平行に入射した電磁波(光)や音は同時に焦点に到達する性質がある5。宇宙の基地局から送られてくる電波がアンテナに平行に入ってくると、放物面である反射器で反射して、焦点部分にあるアンテナの受信器で受信する仕組みになっている(下の左図参照)。
この性質は、天体観測のための「電波望遠鏡」や「反射望遠鏡」、太陽エネルギーを利用した「集光器」や「集熱鏡」(太陽光の集光を利用した温水器の凹面鏡等)、「パラボラマイク」6等の様々な機器に、さらには体内の臓器や結石に超音波を照射する際にも利用されている。
一方で、この性質の逆、即ち焦点から出る電磁波(光)や音は回転放物面に反射すると平行に出ていくことを利用したものが、「車のヘッドライト」や「懐中電灯」となっている。回転放物面の反射板を置くことで、そうでなければ(裸電球のように)四方八方に拡散してしまう光を、平行線として、遠くまで照らすことができる仕組みになっている(下の右図参照)。
回転放物面に平行に入射した電磁波(光)や音は、放物線の焦点のただ一点に集まる(しかも、同時に平行に入射した電磁波(光)や音は同時に焦点に到達する性質がある5。宇宙の基地局から送られてくる電波がアンテナに平行に入ってくると、放物面である反射器で反射して、焦点部分にあるアンテナの受信器で受信する仕組みになっている(下の左図参照)。
この性質は、天体観測のための「電波望遠鏡」や「反射望遠鏡」、太陽エネルギーを利用した「集光器」や「集熱鏡」(太陽光の集光を利用した温水器の凹面鏡等)、「パラボラマイク」6等の様々な機器に、さらには体内の臓器や結石に超音波を照射する際にも利用されている。
一方で、この性質の逆、即ち焦点から出る電磁波(光)や音は回転放物面に反射すると平行に出ていくことを利用したものが、「車のヘッドライト」や「懐中電灯」となっている。回転放物面の反射板を置くことで、そうでなければ(裸電球のように)四方八方に拡散してしまう光を、平行線として、遠くまで照らすことができる仕組みになっている(下の右図参照)。
5 太陽光線に対して回転放物面を利用すると、焦点に置かれたものはすぐに焦げてしまう(このため「焦点」と呼ばれる)。
6 音波を放物面で反射させ、中央のマイクに音波を集中させる集音マイクで、野鳥のさえずりの録音等の際に使用される。
(2023年11月01日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月29日
地域イベントの現実と課題-渋谷のハロウィンをイベントとして運営できるか- -
2025年10月28日
試練の5年に踏み出す中国(前編)-「第15次五カ年計画」の5年間は、どのような5年か -
2025年10月28日
地域医療連携推進法人の現状と今後を考える-「連携以上、統合未満」で協力する形態、その将来像は? -
2025年10月28日
東宝の自己株式取得-公開買付による取得 -
2025年10月28日
今週のレポート・コラムまとめ【10/21-10/27発行分】
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【曲線にはどんな種類があって、どう社会に役立っているのか(その2)-円錐曲線(楕円、放物線、双曲線)が現れる場面-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
曲線にはどんな種類があって、どう社会に役立っているのか(その2)-円錐曲線(楕円、放物線、双曲線)が現れる場面-のレポート Topへ























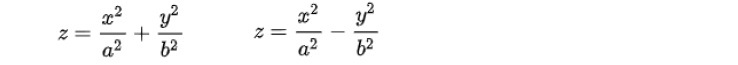


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




