- シンクタンクならニッセイ基礎研究所 >
- ハニカム構造について-ハチの巣はなぜ六角形なのか?-
コラム
2021年07月16日
文字サイズ
- 小
- 中
- 大
はじめに
ハチの巣の1つ1つを正面から見た場合に、それが六角形であることはご存じの方も多いと思われる。でも、なぜ六角形なのかということについては、その理由をご存じの方はそれほど多くはいらっしゃらないものと思われる。
今回のレポートでは、その理由を説明するとともに、このハチの巣で代表される「ハニカム構造」と呼ばれるものが、社会でも幅広く応用されていることについて紹介する。
今回のレポートでは、その理由を説明するとともに、このハチの巣で代表される「ハニカム構造」と呼ばれるものが、社会でも幅広く応用されていることについて紹介する。
「ハニカム構造」とは
それでは、「ハニカム構造」はなぜ、最適な構造になっているのかについて、以下の点、順を追って、説明していくこととする。
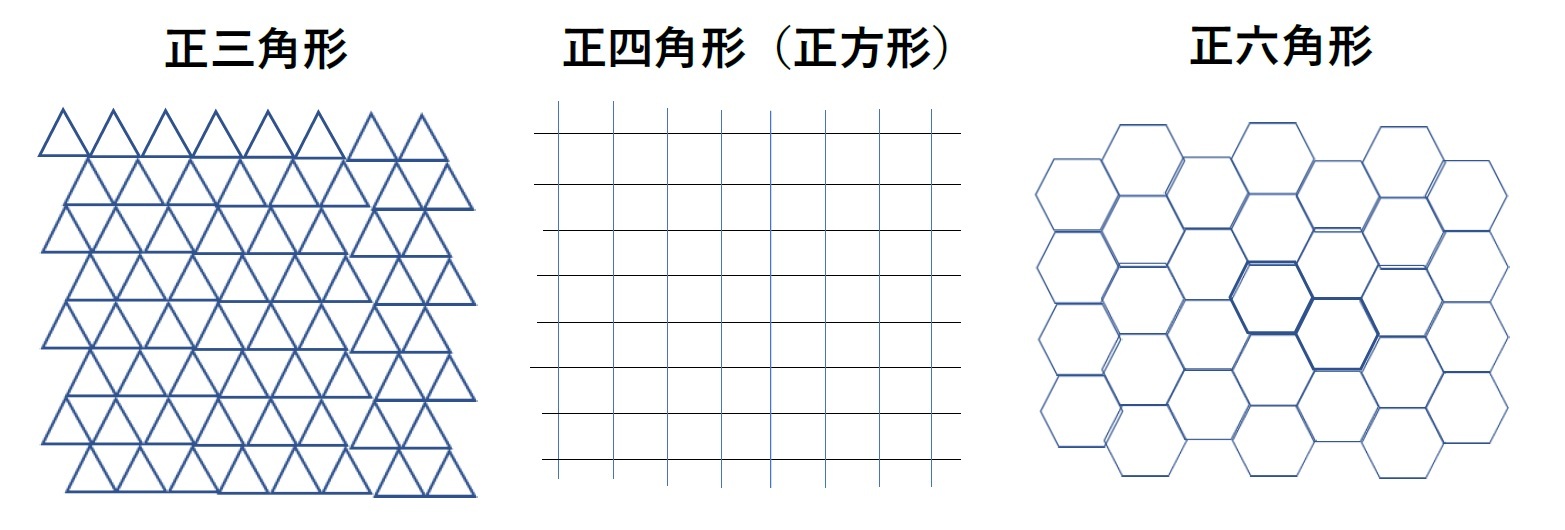
・平面を隙間なく敷き詰めることができる正多角形は、正三角形、正四角形、正六角形しかない。
・外周の長さが一定の多角形の中で、面積が最大となるのは正多角形である。
・外周の長さが一定である場合、正三角形、正四角形、正六角形の中では、正六角形の面積が最大になる。
・正六角形は、強度という面でも一定の水準を確保している。
・平面を隙間なく敷き詰めることができる正多角形は、正三角形、正四角形、正六角形しかない。
・外周の長さが一定の多角形の中で、面積が最大となるのは正多角形である。
・外周の長さが一定である場合、正三角形、正四角形、正六角形の中では、正六角形の面積が最大になる。
・正六角形は、強度という面でも一定の水準を確保している。
まずは「平面充填」(隙間のないタイル張り)という問題
「平面充填」というのは、「平面内を有限種類の平面図形(タイル)で隙間なく敷き詰める操作」のことをいう1。
タイル張りのことを考えれば明らかであるが、ある平面を平面図形で敷き詰めていく場合には、当然に隙間がないことが求められることになる。隙間がないということは、強度という面でも意味がある。
この場合、もちろん、いろんな形の平面図形を多数使用することができるのであれば、無限の敷き詰めのパターンが考えられることになる。ところが、実際の社会での応用を考えれば、できれば数少ない種類の平面図形で敷き詰めることができることが、効率性等の観点からは望まれることになる。もちろん、デザイン性等の観点から、複数の平面図形を使用することも考えられるが、この場合でも一定の規則で隙間なく敷き詰められることが求められることになる。
そこで、ここでは「1種類の正多角形で敷き詰める」という条件を考える。
この場合、「平面充填可能な正多角形は、正三角形、正四角形、正六角形の3種類しかない」ことが示される。
1 「平面充填」は、より一般的な概念である「空間充填」(空間内を図形で隙間なく埋め尽くす操作)の特殊なケース(2次元の場合)である。以下の説においては、基本的には2次元平面のケースを想定して説明している。
タイル張りのことを考えれば明らかであるが、ある平面を平面図形で敷き詰めていく場合には、当然に隙間がないことが求められることになる。隙間がないということは、強度という面でも意味がある。
この場合、もちろん、いろんな形の平面図形を多数使用することができるのであれば、無限の敷き詰めのパターンが考えられることになる。ところが、実際の社会での応用を考えれば、できれば数少ない種類の平面図形で敷き詰めることができることが、効率性等の観点からは望まれることになる。もちろん、デザイン性等の観点から、複数の平面図形を使用することも考えられるが、この場合でも一定の規則で隙間なく敷き詰められることが求められることになる。
そこで、ここでは「1種類の正多角形で敷き詰める」という条件を考える。
この場合、「平面充填可能な正多角形は、正三角形、正四角形、正六角形の3種類しかない」ことが示される。
1 「平面充填」は、より一般的な概念である「空間充填」(空間内を図形で隙間なく埋め尽くす操作)の特殊なケース(2次元の場合)である。以下の説においては、基本的には2次元平面のケースを想定して説明している。
平面充填可能な正多角形が3種類しかない証明
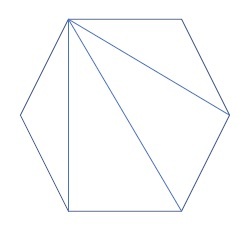
1つの正n角形で平面充填可能であるためには、明らかに複数枚の正多角形を1点の周りに並べた時に360°にならなければならない。
右図の正六角形のケースを見てわかるように、正n角形は(n-2) 個の三角形に分割することができることから、その内角の総和が (n-2)×180°となる。従って、1つの内角の大きさは(n-2)/n×180°となる。
右図の正六角形のケースを見てわかるように、正n角形は(n-2) 個の三角形に分割することができることから、その内角の総和が (n-2)×180°となる。従って、1つの内角の大きさは(n-2)/n×180°となる。
(参考)さらなる平面充填のパターン
なお、正多角形に限定せずに、変形した多角形を許容する場合には、さらに別の「1種類の多角形で敷き詰める」パターンも考えられることになる。代表的なパターンとしては、平行四辺形が該当するが、それ以外にも数多くのパターンが考えられる。
また、1種類ではなく「2種類以上の正多角形で敷き詰める場合」も考えられることになる。この場合には、可能な組み合わせは8つのケースしかない、ことが知られている。これらの内容については、別途の研究員の眼で報告することとして、ここではこれ以上詳しくは触れないこととする。
なお、正多角形に限定せずに、変形した多角形を許容する場合には、さらに別の「1種類の多角形で敷き詰める」パターンも考えられることになる。代表的なパターンとしては、平行四辺形が該当するが、それ以外にも数多くのパターンが考えられる。
また、1種類ではなく「2種類以上の正多角形で敷き詰める場合」も考えられることになる。この場合には、可能な組み合わせは8つのケースしかない、ことが知られている。これらの内容については、別途の研究員の眼で報告することとして、ここではこれ以上詳しくは触れないこととする。
いわゆる「等周問題」について
これまでは、あくまでも「正多角形」のケースを考えてきた。ただし、なぜ正多角形なのか、正多角形以外に、より効率的な多角形のパターンは存在しないのか、と思われる方もおられるかもしれない。ここでは、この問題を説明する。
いわゆる「等周問題(isoperimetric problem)」と呼ばれるのは、「外周の長さが与えられた平面図形の中で最大の面積をもつものは何か」とか、「表面積が与えられた立体の中で最大の体積をもつものを何か」という問題である。これらの問いに対する解は、直感的にも一定程度は推定できると思われるが、それぞれ「円」や「球」になる(この点をここで証明することは容易ではないので、ここでは結果だけを受け入れてもらうこととする)。
これによれば、逆に言えば「同じ面積で最も外周が短い図形は円」ということになる。ところが、明らかに円だけでは(隙間ができてしまい)平面全体を充填することはできない。
そこで、次に、多角形のケースを考える。これについても、「外周の長さが一定である多角形の中で、面積が最大のものは正多角形である」ことが知られている。これについての一般的なケースの証明は容易ではないので、ここでは三角形のケースを示しておく。
いわゆる「等周問題(isoperimetric problem)」と呼ばれるのは、「外周の長さが与えられた平面図形の中で最大の面積をもつものは何か」とか、「表面積が与えられた立体の中で最大の体積をもつものを何か」という問題である。これらの問いに対する解は、直感的にも一定程度は推定できると思われるが、それぞれ「円」や「球」になる(この点をここで証明することは容易ではないので、ここでは結果だけを受け入れてもらうこととする)。
これによれば、逆に言えば「同じ面積で最も外周が短い図形は円」ということになる。ところが、明らかに円だけでは(隙間ができてしまい)平面全体を充填することはできない。
そこで、次に、多角形のケースを考える。これについても、「外周の長さが一定である多角形の中で、面積が最大のものは正多角形である」ことが知られている。これについての一般的なケースの証明は容易ではないので、ここでは三角形のケースを示しておく。
外周の長さが一定である三角形の中で,面積が最大のものが正三角形であることの証明
ここで、等号が成立するのは、s−a=s−b=s−c の場合、つまり正三角形の場合となる。
それでは、なぜ「正三角形」や「正四角形」ではなく、「正六角形」なのか
ここでは、外周の長さが一定の場合に、正三角形、正四角形、正六角形の面積の関係がどのようになるのかを見てみる。
外周の長さを1とした場合、各ケースの正多角形の面積は、以下の通りとなる。
(1) 正三角形の場合
1辺の長さは1/3であることから、その面積は、
底辺×高さ÷2=(1/3×1/3×√3/2)÷2=√3/24
(2) 正四角形の場合
1辺の長さは1/4であることから、その面積は、
1/4×1/4=1/16
(3) 正六角形の場合
1辺の長さは1/6であり、P2の図で示したように6つの正三角形に分割できることから、その面積は、
((1/6×1/6×√3/2)÷2)×6=√ 3/16
以上の結果において、大小関係は以下の通りとなる。
√3/24 < 1/16 < √3/16
以上より、「外周の長さが一定の場合、正三角形、正四角形(正方形)、正六角形の中では、正六角形の場合に面積が最大になる」ことになる。
外周の長さを1とした場合、各ケースの正多角形の面積は、以下の通りとなる。
(1) 正三角形の場合
1辺の長さは1/3であることから、その面積は、
底辺×高さ÷2=(1/3×1/3×√3/2)÷2=√3/24
(2) 正四角形の場合
1辺の長さは1/4であることから、その面積は、
1/4×1/4=1/16
(3) 正六角形の場合
1辺の長さは1/6であり、P2の図で示したように6つの正三角形に分割できることから、その面積は、
((1/6×1/6×√3/2)÷2)×6=√ 3/16
以上の結果において、大小関係は以下の通りとなる。
√3/24 < 1/16 < √3/16
以上より、「外周の長さが一定の場合、正三角形、正四角形(正方形)、正六角形の中では、正六角形の場合に面積が最大になる」ことになる。
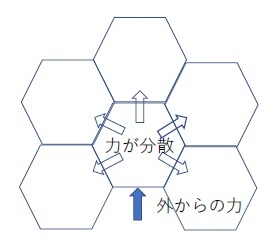
「ハニカム構造」は、強度の観点からはどうなのか
さて、ここまでは、「材料の効率的活用」という観点に焦点を当てて、「ハニカム構造」の有用性を説明してきた。それでは、この「ハニカム構造」は「強度」という観点ではどうなのか、という点が気になるかもしれない。
この点に関して、まずは断面が正三角形、正四角形(正方形)、正六角形の形を有する角柱の上に物を載せる場合、正n角形のnが大きくなるほど強度が増すことになると言われている。これによれば、この意味での強度は円柱が最も高いことになる。
次に、側面等の一定方向からの力に対する強度はどうなのだろうか。
正三角形は、各種の方向からの力に対して、安定しており、その意味での「強度」では最も優れていると言われているようである。その意味では、(「材料の効率的活用」を考慮しなければ)正六角形そのものよりも、その中に6つの正三角形を組み入れた方がより強度が高くなると言えることになるのかもしれない。
この点に関して、まずは断面が正三角形、正四角形(正方形)、正六角形の形を有する角柱の上に物を載せる場合、正n角形のnが大きくなるほど強度が増すことになると言われている。これによれば、この意味での強度は円柱が最も高いことになる。
次に、側面等の一定方向からの力に対する強度はどうなのだろうか。
正三角形は、各種の方向からの力に対して、安定しており、その意味での「強度」では最も優れていると言われているようである。その意味では、(「材料の効率的活用」を考慮しなければ)正六角形そのものよりも、その中に6つの正三角形を組み入れた方がより強度が高くなると言えることになるのかもしれない。
ハチの巣が六角形である理由
以上、ここまでの説明で、ある一定の面積の平面を隙間なく敷き詰める場合において、「正六角形」による場合が、最も外周が小さくでき、即ち(外周を構成する)材料を効率的に使用できることがわかった。さらに、「正六角形」は強度の面でも一定の水準を確保していることがわかった。
従って、ハチの巣のケースに戻って考えてみると、一定の強度を保ちつつ、最も少ない蜜蠟(honey wax)で、できる限り広い巣を作ることができるのは、「正六角形」の場合だということになる。蜜蠟を作り出すのは容易なことではなく、約220gの蜜から、やっと約30gの蜜蝋を作り出すことができると言われているようだ。さらに、一匹のミツバチが生涯で集める蜂蜜の量はスプーン一杯の約5gだと言われているようだ。従って、いかに効率的に蜜を利用するのかはハチにとって極めて重要な意味を有していることになる。
ハチがこのようなことをどのような形で会得してきたのかはわからないが、ただ自然界の生物は、その進化の過程等を通じて、こうしたバランスの取れた最適な方式を自然に体得し、巧みに利用して生きていることがわかる。
従って、ハチの巣のケースに戻って考えてみると、一定の強度を保ちつつ、最も少ない蜜蠟(honey wax)で、できる限り広い巣を作ることができるのは、「正六角形」の場合だということになる。蜜蠟を作り出すのは容易なことではなく、約220gの蜜から、やっと約30gの蜜蝋を作り出すことができると言われているようだ。さらに、一匹のミツバチが生涯で集める蜂蜜の量はスプーン一杯の約5gだと言われているようだ。従って、いかに効率的に蜜を利用するのかはハチにとって極めて重要な意味を有していることになる。
ハチがこのようなことをどのような形で会得してきたのかはわからないが、ただ自然界の生物は、その進化の過程等を通じて、こうしたバランスの取れた最適な方式を自然に体得し、巧みに利用して生きていることがわかる。
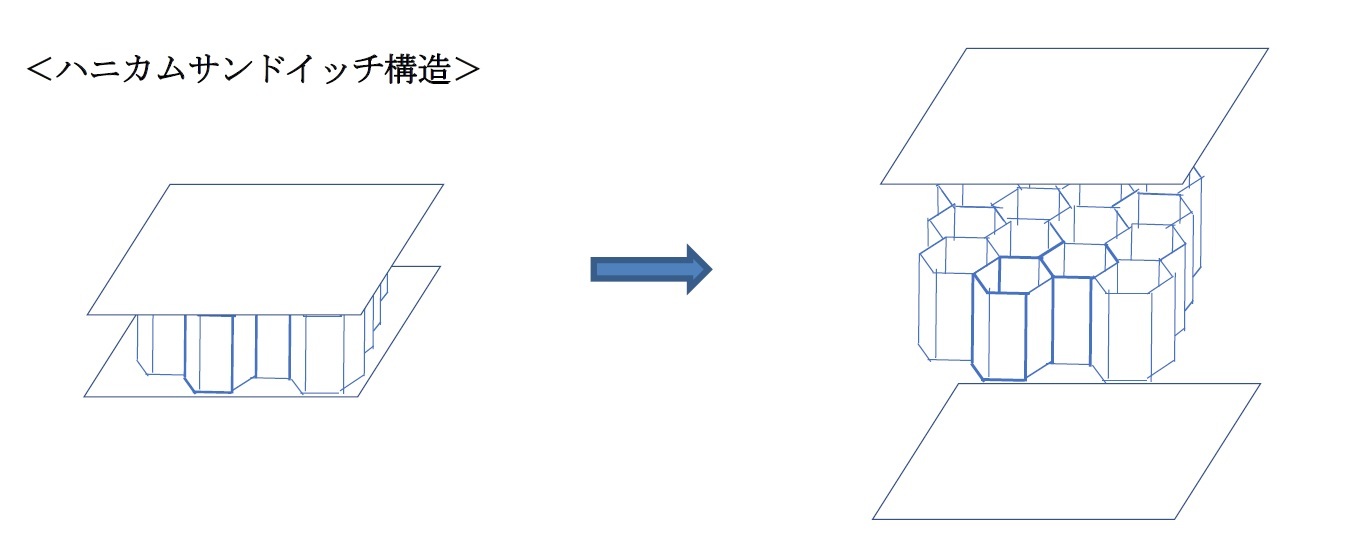
「ハニカム構造」の応用例
また、原子レベルにおいては、炭素同士の六角形での結合が強度を生み出すことから、「カーボンナノチューブ」は全体がその六角形の結合から構成され、その軽さ、細さ、柔軟性に対して、強度が強く、さらに非常に高い導電性、熱伝導性・耐熱性を有していることから、次世代の炭素素材として、様々な用途向けの開発が行われてきている。
これ以外に有名なものとして、「サッカーのゴールネット」の例が挙げられる。以前は格子状(四角形)のネットが使用されていたが、2000年頃からハニカム状(六角形)のネットが使用されるようになっている。この理由としては、シュートしたボールがゴールに突き刺さってネットに絡みとられて、ダイナミックなゴールシーンが見えるという演出的な理由が挙げられているようだ。この背景には、(1)(先に述べたように)四角形の場合に比べて、六角形の場合には同じ空間を埋めるのに必要なネットの量が少なくて済むことから、ネットを通じて向こう側が見やすくなっているとか、(2)ネットの伸縮の方向がより幅広くなっていることから、ボールがネットにあまり影響されずにより自然にゴールに吸い込まれていける、というような事実が関係していることになる。
2 ロケットの最先端部に位置し、打ち上げの際の大きな音響や振動、大気中を飛行する際に生じる摩擦熱から衛星を護る役割を果たしているもの
これ以外に有名なものとして、「サッカーのゴールネット」の例が挙げられる。以前は格子状(四角形)のネットが使用されていたが、2000年頃からハニカム状(六角形)のネットが使用されるようになっている。この理由としては、シュートしたボールがゴールに突き刺さってネットに絡みとられて、ダイナミックなゴールシーンが見えるという演出的な理由が挙げられているようだ。この背景には、(1)(先に述べたように)四角形の場合に比べて、六角形の場合には同じ空間を埋めるのに必要なネットの量が少なくて済むことから、ネットを通じて向こう側が見やすくなっているとか、(2)ネットの伸縮の方向がより幅広くなっていることから、ボールがネットにあまり影響されずにより自然にゴールに吸い込まれていける、というような事実が関係していることになる。
2 ロケットの最先端部に位置し、打ち上げの際の大きな音響や振動、大気中を飛行する際に生じる摩擦熱から衛星を護る役割を果たしているもの
(2021年07月16日「研究員の眼」)
このレポートの関連カテゴリ
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月28日
今週のレポート・コラムまとめ【10/21-10/27発行分】 -
2025年10月27日
秋の夜長に市民と経済の主食を考える-農業と電力はこれからも日本の食欲を満たせるのか -
2025年10月27日
大学卒女性の働き方別生涯賃金の推計(令和6年調査より)-正社員で2人出産・育休・時短で2億円超 -
2025年10月27日
なぜ味噌汁は動くのか -
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【ハニカム構造について-ハチの巣はなぜ六角形なのか?-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
ハニカム構造について-ハチの巣はなぜ六角形なのか?-のレポート Topへ



















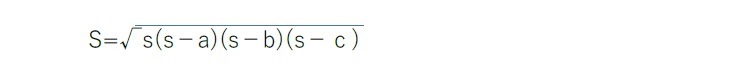
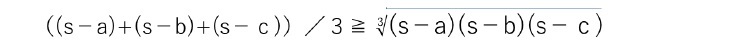



 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




