- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- フラクタルって知っていますか-1.26次元や1.58次元の図形ってどんなものなのだろう-
コラム
2021年06月28日
文字サイズ
- 小
- 中
- 大
はじめに
「フラクタル」という言葉を聞いたことがあるだろうか。実は、このコラムでも「フィボナッチ数列について(その3)-フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか(自然界以外)-」(2021.3.26)の最後に、フィボナッチ数列との関連の中で若干触れておいた。
今回は、この「フラクタル」という概念及びそれが自然界等でどのように観測され、またそれが社会でどのように利用されているのかについて、紹介する。
まずは、今回の研究員の眼では、「フラクタル」という概念及び代表的な「フラクタル図形」について紹介する。
今回は、この「フラクタル」という概念及びそれが自然界等でどのように観測され、またそれが社会でどのように利用されているのかについて、紹介する。
まずは、今回の研究員の眼では、「フラクタル」という概念及び代表的な「フラクタル図形」について紹介する。
フラクタルとは
「フラクタル(fractal)」というのは、「自己相似性」という特殊な性質を有する幾何学的構造のことをいい、より具体的には「図形の全体をいくつかの部分に分解していった時に全体と同じ形が再現されていく構造」のことをいう。フランス人の数学者ブノワ・マンデルブロ(Benoît B. Mandelbrot)が考案した概念である1。フラクタル構造を有する図形が「フラクタル図形」となる。
自然は一見すると無秩序なカオス状態のようにみえるが、よく観察すると同じ構造が繰り返されている「フラクタル構造」になっている(ものが多く観察される)と言われている。
1 因みに、「フラクタル(fractal)」は、ラテン語の「フラクタス(fractus)」から作られたマンデルプロの造語であり、英語の「一部・断片・破片」等の意味を有する「フラクション(fraction)」と同じ語源となっている。
自然は一見すると無秩序なカオス状態のようにみえるが、よく観察すると同じ構造が繰り返されている「フラクタル構造」になっている(ものが多く観察される)と言われている。
1 因みに、「フラクタル(fractal)」は、ラテン語の「フラクタス(fractus)」から作られたマンデルプロの造語であり、英語の「一部・断片・破片」等の意味を有する「フラクション(fraction)」と同じ語源となっている。
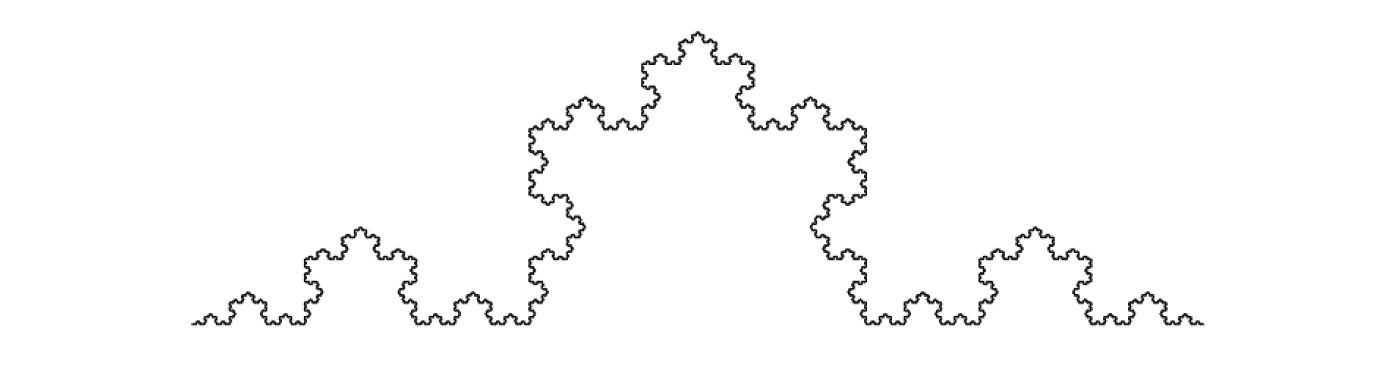
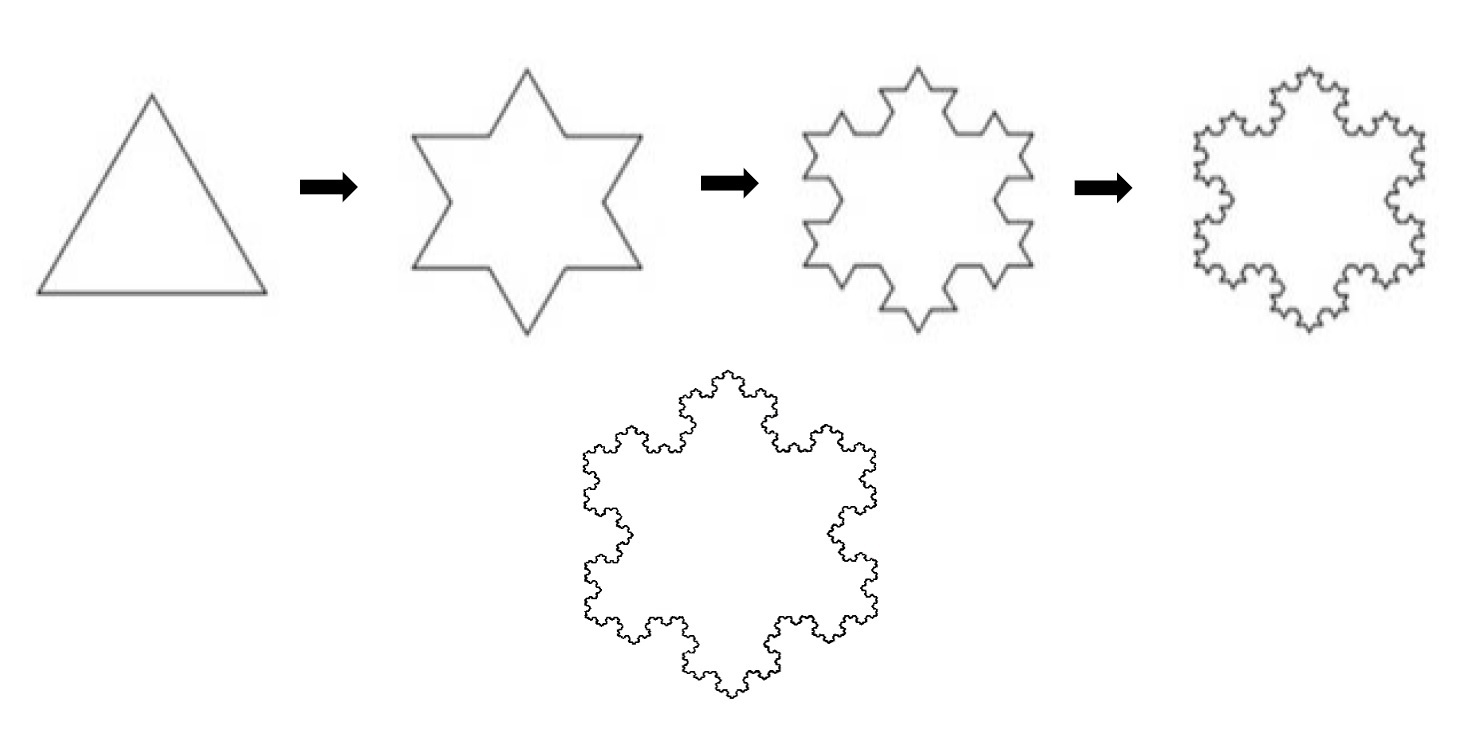
コッホ曲線
このコッホ曲線について、その長さを測定してみると、1回の操作で線分の長さが 4/3 倍になるので、操作を無限に繰り返して得られるコッホ曲線の長さは無限大となる。
コッホ曲線は無限の長さを持つので、同様にコッホ雪片の周長(周囲の長さ)も無限の長さを持つ。一方で、コッホ雪片の曲線で囲まれた面積は有限に留まる。最初の正三角形の面積を 1 とするとコッホ雪片の面積は 1.6 に収束する。
となり、元の正三角形の1.6倍となる。
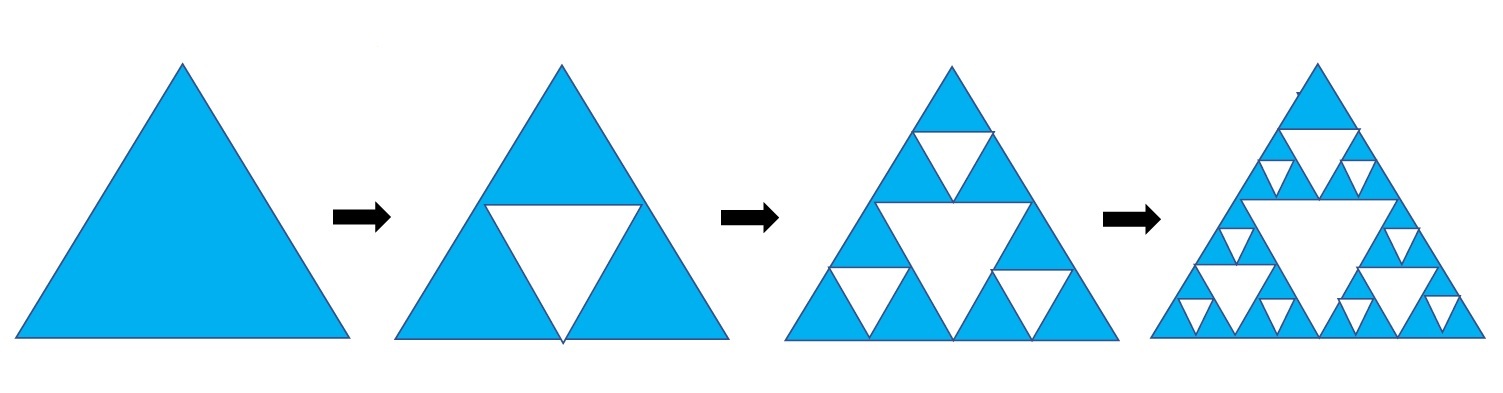
シェルピンスキーの三角形
もう一つ有名なフラクタル図形として「シェルピンスキーの三角形」を紹介しておく。これは、「シェルピンスキーのギャスケット(Sierpiński gasket)」とも呼ばれるもので、自己相似的な無数の三角形からなる図形である。1915年にポーランドの数学者ヴァツワフ・シェルピンスキー(Wacław Franciszek Sierpiński)によって考案された。
これは、以下の手順を繰り返すことで作図される。
(1) 正三角形を用意する。
(2) 正三角形の各辺の中点を互いに結んでできた中央の正三角形を切り取る。
(3) 残った正三角形に対して、(2)の手順を無限に繰り返す。
具体的に、例えば4段階までの過程を示すと、以下の通りとなる。
これは、以下の手順を繰り返すことで作図される。
(1) 正三角形を用意する。
(2) 正三角形の各辺の中点を互いに結んでできた中央の正三角形を切り取る。
(3) 残った正三角形に対して、(2)の手順を無限に繰り返す。
具体的に、例えば4段階までの過程を示すと、以下の通りとなる。
この図形の面積は明らかに有限であるが、この図形を構成している正三角形の3辺の長さは、上記の図からわかるように、1回の操作で1.5倍になっていくことから、無限に大きくなっていく。
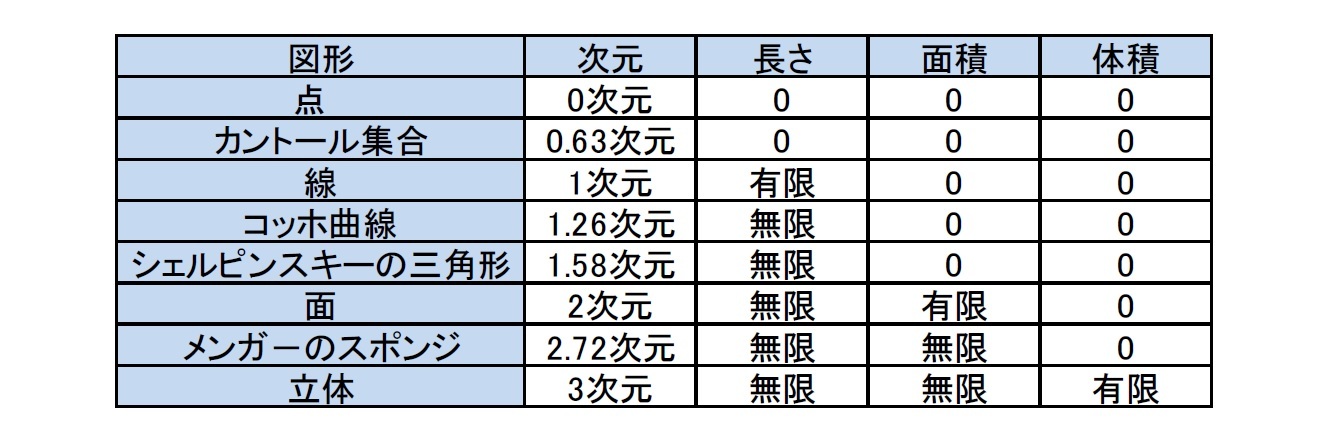
フラクタル次元
通常「次元」といえば、1次元の直線、2次元の平面、3次元の空間、さらにはこれに時間の概念を加えた4次元といったものを思い浮かべると思われる。ところが、フラクタルの世界においては、「フラクタル次元」という概念が存在し、ここで定義される次元は0以上の実数で整数であるとは限らない。
具体的に、あるフラクタル図形の「フラクタル次元がnである」とは、「相似比が1:aである時に、いわゆる『長さ』の比が1:b となる時の an=b となるnのこと」を言う。
別の定義では、「あるフラクタル図形を1/a に縮小したときに、元の図形を埋めるために必要となる図形の個数がbとなる時のan=b となるnのこと」を言う。
これがいわゆる通常の次元の拡張概念になっていることは、2次元平面では「相似比が1:2になるときに、長さが1:4になっていく」ということから、ご理解いただけるのではないかと思う。
いずれにしても、フラクタル次元は「n=log b/log a 」で定義されることになる。
線の図形は、平面を覆い尽くすように複雑になればなるほど、平面に近くなるので、フラクタル次元は「2」に近くなることになる。このことから、線の図形が平面を覆っている割合を、フラクタル次元を用いて表すことができることになる。
さて、先ほどの「コッホ曲線」を例にとると、図を見ていただければわかるように、a=3、b=4 となるので、 log 4/log 3 ≒1.2618 となる。即ち、「コッホ曲線」は、1.26次元の図形ということになる。
これに対して、「シェルピンスキーの三角形」の場合には、a=2、b=3 となるので、log 3/log 2 ≒1.5849 となる。即ち、「シェルピンスキーの三角形」は、1.58次元の図形ということになる。
従って、「シェルピンスキーの三角形」は「コッホ曲線」や「コッホ雪片」と比べて密である、といえることになる。
具体的に、あるフラクタル図形の「フラクタル次元がnである」とは、「相似比が1:aである時に、いわゆる『長さ』の比が1:b となる時の an=b となるnのこと」を言う。
別の定義では、「あるフラクタル図形を1/a に縮小したときに、元の図形を埋めるために必要となる図形の個数がbとなる時のan=b となるnのこと」を言う。
これがいわゆる通常の次元の拡張概念になっていることは、2次元平面では「相似比が1:2になるときに、長さが1:4になっていく」ということから、ご理解いただけるのではないかと思う。
いずれにしても、フラクタル次元は「n=log b/log a 」で定義されることになる。
線の図形は、平面を覆い尽くすように複雑になればなるほど、平面に近くなるので、フラクタル次元は「2」に近くなることになる。このことから、線の図形が平面を覆っている割合を、フラクタル次元を用いて表すことができることになる。
さて、先ほどの「コッホ曲線」を例にとると、図を見ていただければわかるように、a=3、b=4 となるので、 log 4/log 3 ≒1.2618 となる。即ち、「コッホ曲線」は、1.26次元の図形ということになる。
これに対して、「シェルピンスキーの三角形」の場合には、a=2、b=3 となるので、log 3/log 2 ≒1.5849 となる。即ち、「シェルピンスキーの三角形」は、1.58次元の図形ということになる。
従って、「シェルピンスキーの三角形」は「コッホ曲線」や「コッホ雪片」と比べて密である、といえることになる。
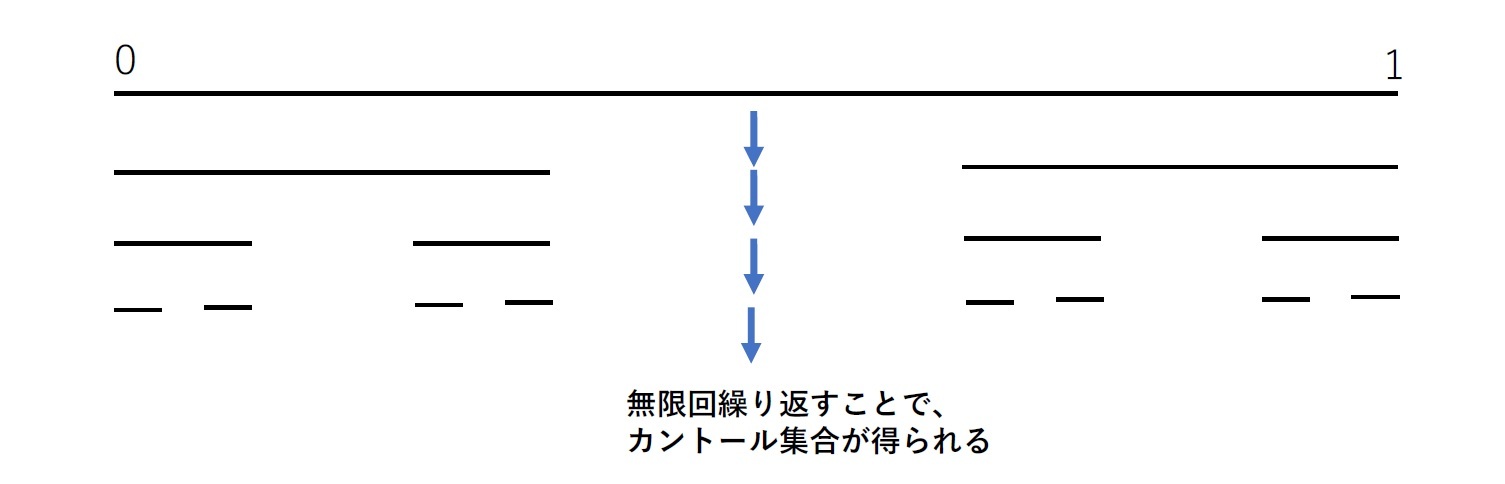
カントール集合
上記の2つは、1次元超2次元未満のフラクタル図形となっていた。ここでは、1次元未満のフラクタル図形の例として、「カントール集合」を紹介する。
「カントール集合(Cantor set)」というのは、「閉区間 [0, 1] に属する実数のうち、その三進展開のどの桁にも 1 が含まれないような表示ができるもの全体からなる集合」のことをいう。これだと何だかよくわからないということになると思われるので、幾何学的に示すと、次ページの図のようになる。
以下のように、線分を3等分し、得られた3つの線分の真ん中のものを取り除くという操作を繰り返す。即ち、単位区間I = [0, 1] から、1回目の操作で (1/3, 2/3) を取り除き、2回目の操作で (1/9, 2/9) と (7/9, 8/9) を取り除き……といった具合に操作を無限に繰り返していって残った部分が「カントール集合」となる。
「カントール集合(Cantor set)」というのは、「閉区間 [0, 1] に属する実数のうち、その三進展開のどの桁にも 1 が含まれないような表示ができるもの全体からなる集合」のことをいう。これだと何だかよくわからないということになると思われるので、幾何学的に示すと、次ページの図のようになる。
以下のように、線分を3等分し、得られた3つの線分の真ん中のものを取り除くという操作を繰り返す。即ち、単位区間I = [0, 1] から、1回目の操作で (1/3, 2/3) を取り除き、2回目の操作で (1/9, 2/9) と (7/9, 8/9) を取り除き……といった具合に操作を無限に繰り返していって残った部分が「カントール集合」となる。
このカントール集合については、自分自身を 1/3倍に縮小したものを 2個持ってくれば自分自身を再構成できるので、自己相似性を有するフラクタル図形である。そのフラクタル次元は、log2/log3 ≒0.6309 となり、0.63次元の図形ということになる。即ち、通常の直線の2/3未満の次元しか有していないことになる。
メンガーのスポンジ
ここでは、2次元超3次元未満のフラクタル図形の例として、「メンガーのスポンジ」を紹介する。
「メンガーのスポンジ(Menger sponge)」というのは、以下のプロセスで作成される図形2である。
(1) 立方体を、3×3×3の27個の区画に分け、中央(面心・体心)の7個を取り除く。
(2) 残った小さな20個の立方体に対して同じ事を繰り返していく。
「メンガーのスポンジ」のフラクタル次元は、log20/log3=2.7268 となり、2.72次元の図形ということになる。
「メンガーのスポンジ」は、1回のプロセスでその表面積が1/3ずつ増加することになるため、その(2次元的な大きさを示す)表面積は無限となる。一方で、1回のプロセスでその体積は7/27ずつ減少することになるため、その(3次元的な大きさを示す)体積は0となる。
「メンガーのスポンジ(Menger sponge)」というのは、以下のプロセスで作成される図形2である。
(1) 立方体を、3×3×3の27個の区画に分け、中央(面心・体心)の7個を取り除く。
(2) 残った小さな20個の立方体に対して同じ事を繰り返していく。
「メンガーのスポンジ」のフラクタル次元は、log20/log3=2.7268 となり、2.72次元の図形ということになる。
「メンガーのスポンジ」は、1回のプロセスでその表面積が1/3ずつ増加することになるため、その(2次元的な大きさを示す)表面積は無限となる。一方で、1回のプロセスでその体積は7/27ずつ減少することになるため、その(3次元的な大きさを示す)体積は0となる。
このように、フラクタル図形については、伝統的な図形の基準指標である「長さ」、「面積」、「体積」とは異なるこれらの中間に位置する指標が存在して、それが有限となるものとして存在している形になっていることがわかる。
まとめ
以上、今回は「フラクタル」という概念及び代表的なフラクタル図形について紹介してきた。
今回紹介したもの以外にも、「ドラゴン曲線(Dragon curve)」と呼ばれる図形、「バーンズリーのシダ(Barnsley fern)」と呼ばれるシダを模した図形、「シェルピンスキーのカーペット(Sierpiński carpet)」等が有名なフラクタル図形である。さらには、コッホ曲線やシェルピンスキーの三角形の立体版である「コッホの双正三角錐」や「シェルピンスキーの四面体」等も存在する。
ここまでに紹介したこれらのフラクタル図形は、出発点となる図形をコピーして、主として「相似変換(辺の長さの比や角度を変えずに大きさを変更)」を繰り返すことによって作成される「反復関数系(IFS:Iterated function system)フラクタル」と呼ばれるものである。
さらには、別の作成方法によるフラクタル図形もある。出発点となる図形をコピーして、「反転」と呼ばれる変換による縮小を繰り返して作成する「円反転フラクタル」と呼ばれるものとして「アポロニウスのギャスケット(Apollonian gasket)」や、複素数を使った漸化式を使用して作成する「複素力学系フラクタル」と呼ばれるものとして「マンデルブロ集合(Mandelbrot set)」や「ジュリア集合(Julia set)」といったものもある。興味を感じられた方は、是非こうした図形もご覧になられると面白く感じられるのではないかと思う。
なお、「フラクタル」というのは、ここまで説明してきたように抽象的な数学の概念であるが、一方で実は、このフラクタルが自然界に広くみられることがわかっている。
このシリーズの次回の研究員の眼では、自然界でみられるフラクタルについて紹介することとしたい。
今回紹介したもの以外にも、「ドラゴン曲線(Dragon curve)」と呼ばれる図形、「バーンズリーのシダ(Barnsley fern)」と呼ばれるシダを模した図形、「シェルピンスキーのカーペット(Sierpiński carpet)」等が有名なフラクタル図形である。さらには、コッホ曲線やシェルピンスキーの三角形の立体版である「コッホの双正三角錐」や「シェルピンスキーの四面体」等も存在する。
ここまでに紹介したこれらのフラクタル図形は、出発点となる図形をコピーして、主として「相似変換(辺の長さの比や角度を変えずに大きさを変更)」を繰り返すことによって作成される「反復関数系(IFS:Iterated function system)フラクタル」と呼ばれるものである。
さらには、別の作成方法によるフラクタル図形もある。出発点となる図形をコピーして、「反転」と呼ばれる変換による縮小を繰り返して作成する「円反転フラクタル」と呼ばれるものとして「アポロニウスのギャスケット(Apollonian gasket)」や、複素数を使った漸化式を使用して作成する「複素力学系フラクタル」と呼ばれるものとして「マンデルブロ集合(Mandelbrot set)」や「ジュリア集合(Julia set)」といったものもある。興味を感じられた方は、是非こうした図形もご覧になられると面白く感じられるのではないかと思う。
なお、「フラクタル」というのは、ここまで説明してきたように抽象的な数学の概念であるが、一方で実は、このフラクタルが自然界に広くみられることがわかっている。
このシリーズの次回の研究員の眼では、自然界でみられるフラクタルについて紹介することとしたい。
本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2021年06月28日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【フラクタルって知っていますか-1.26次元や1.58次元の図形ってどんなものなのだろう-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
フラクタルって知っていますか-1.26次元や1.58次元の図形ってどんなものなのだろう-のレポート Topへ



















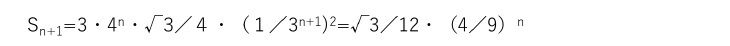
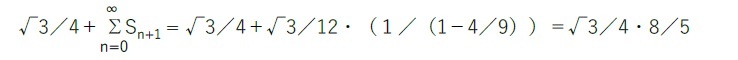


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




