- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- フィボナッチ数列について(その3)-フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか(自然界以外)-
コラム
2021年03月26日
文字サイズ
- 小
- 中
- 大
はじめに
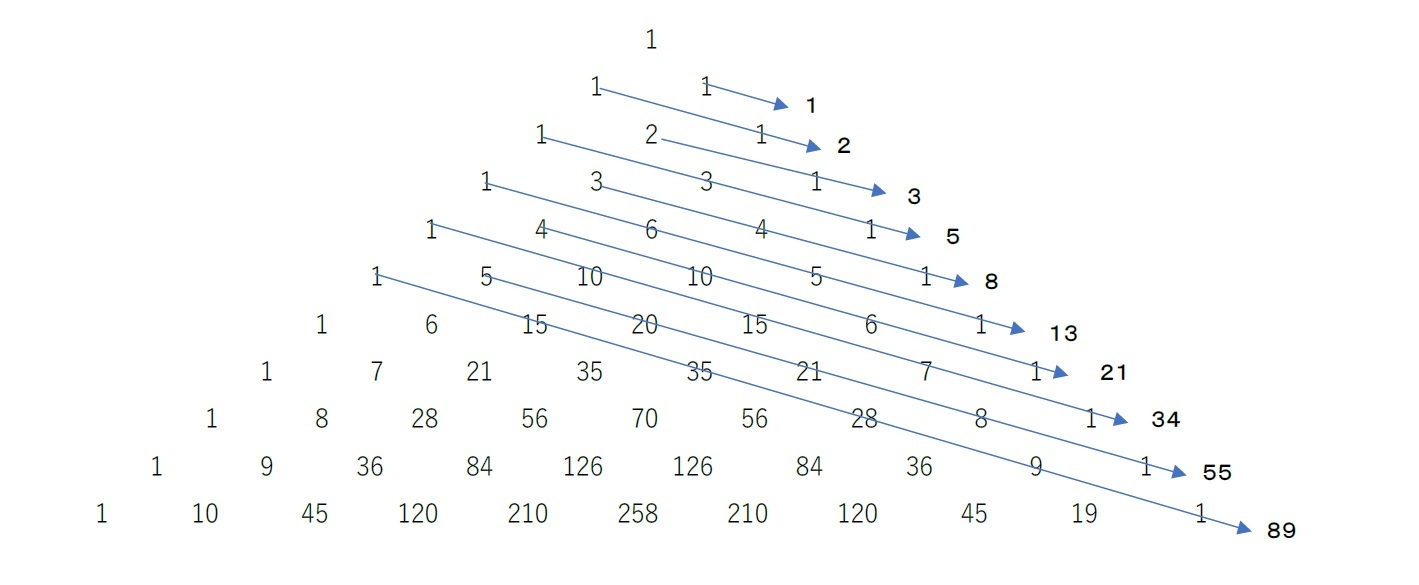
一方で、このパスカルの三角形において、桂馬跳びの様に斜め方向に数字を拾い、その合計を取るとフィボナッチ数になる。例えば、上の図の5+20+21+8+1=55 はフィボナッチ数になっているというような具合である。
一山崩し
「一山崩し」というゲームは、以下のようなルールを有するゲームである。
それは、「残された玉の数がフィボナッチ数になると、その時点で必ず後手必勝になる」ということである。実際に考えてみると、以下のような具合である。
(1) 3個の玉がある場合、先手が1個取れば後手は残りの2個、先手が2個取れば後手は残りの1個を取ればよいので明らかである。
(2) 次に、5個の玉がある場合、先手が1個取れば後手は1個取ることで①の状況になる。先手が2個以上とれば後手は残りの玉を取ればよい。
(3) 8個の玉がある場合、先手が1個取れば後手は2個取ることで(2)の状況になる。先手が2個取れば後手は1個取って(2)の状況になり、先手が3個以上取れば、後手は残りの玉を取ればよい。
(4) 13個の玉がある場合、先手が1個取れば後手は1個取ることで残りは11個となるが、次に先手は1個か2個しか取れないのでいずれにしてもその後後手が2個ないしは1個取ることで(3)の状況になる。先手が2個取れば後手は3個取れば(3)の状況になる。
(5) 1個の玉がある場合、先手が3個((21-13)÷3))以上の玉を取る場合には後手は④の状況に持っていくことができ、先手が3個未満の玉しか取らない場合には、例えば21=8+13 と考えて、(3)と(4)の手法を用いることができる。
このようにして、先手の取る個数に応じて、フィボナッチ数の分解を考えて、後手は常に残りの玉の個数がいくつかのステップを踏むことでフィボナッチ数になるようにしておけば(また、そのことはフィボナッチ数列が前2項の和であり、相手の2倍までしか玉が取れないというルールにより常に可能となる)、先手がいくつの個数を取ろうが後手は必ず残りの玉の個数をフィボナッチ数とするように持っていくことができて、必ず勝てることになる。
従って、逆に言えば、「最初の玉の数がフィボナッチ数でなければ、先手は残りの玉の個数がフィボナッチ数となるように最初に必要な個数を取れば、先手必勝」ということになる。
このように、このゲームは、最初の玉の個数で先手必勝か後手必勝かが決まることになる。
・n個の玉がある。2人が交互に玉を取り合って、最後に玉を取り尽くした方が勝ちとなる。
・最初は、全ての玉を取ることはできないが、任意の個数の玉を取ってもよい。
・各段階で、直前に相手が取った玉の数の2倍まで取ることができる。
それは、「残された玉の数がフィボナッチ数になると、その時点で必ず後手必勝になる」ということである。実際に考えてみると、以下のような具合である。
(1) 3個の玉がある場合、先手が1個取れば後手は残りの2個、先手が2個取れば後手は残りの1個を取ればよいので明らかである。
(2) 次に、5個の玉がある場合、先手が1個取れば後手は1個取ることで①の状況になる。先手が2個以上とれば後手は残りの玉を取ればよい。
(3) 8個の玉がある場合、先手が1個取れば後手は2個取ることで(2)の状況になる。先手が2個取れば後手は1個取って(2)の状況になり、先手が3個以上取れば、後手は残りの玉を取ればよい。
(4) 13個の玉がある場合、先手が1個取れば後手は1個取ることで残りは11個となるが、次に先手は1個か2個しか取れないのでいずれにしてもその後後手が2個ないしは1個取ることで(3)の状況になる。先手が2個取れば後手は3個取れば(3)の状況になる。
(5) 1個の玉がある場合、先手が3個((21-13)÷3))以上の玉を取る場合には後手は④の状況に持っていくことができ、先手が3個未満の玉しか取らない場合には、例えば21=8+13 と考えて、(3)と(4)の手法を用いることができる。
このようにして、先手の取る個数に応じて、フィボナッチ数の分解を考えて、後手は常に残りの玉の個数がいくつかのステップを踏むことでフィボナッチ数になるようにしておけば(また、そのことはフィボナッチ数列が前2項の和であり、相手の2倍までしか玉が取れないというルールにより常に可能となる)、先手がいくつの個数を取ろうが後手は必ず残りの玉の個数をフィボナッチ数とするように持っていくことができて、必ず勝てることになる。
従って、逆に言えば、「最初の玉の数がフィボナッチ数でなければ、先手は残りの玉の個数がフィボナッチ数となるように最初に必要な個数を取れば、先手必勝」ということになる。
このように、このゲームは、最初の玉の個数で先手必勝か後手必勝かが決まることになる。
n 段の階段を1段または2段ずつ上る方法
n 段の階段を1段または2段ずつ上るときに、上る方法の数を Fn+1 通りとすると、Fnはフィボナッチ数列となる。
これは数学的帰納法で証明できる。
n=1 の時は、1段上りの1通りしかないのでF2=1で正しい。
n=2 の時は、1段上りと2段上りの2通りがあるので、F3=2で正しい。
n=k及びn=k+1の時に正しいとする。
(k+2)段に上るためには、(1)k段から2段上りする、(2)(k+1)段から1段上りする、の2つの方法があるが、(1)の場合の、k段までの上り方はFk+1 通りあり、(2)の(k+1)段までの上り方はFk+2 通りある。
従って、(k+2)段に上る方法は、
Fk+1 +Fk+2 =Fk+3
となり、n=k+2 の時も正しくなる。
これは数学的帰納法で証明できる。
n=1 の時は、1段上りの1通りしかないのでF2=1で正しい。
n=2 の時は、1段上りと2段上りの2通りがあるので、F3=2で正しい。
n=k及びn=k+1の時に正しいとする。
(k+2)段に上るためには、(1)k段から2段上りする、(2)(k+1)段から1段上りする、の2つの方法があるが、(1)の場合の、k段までの上り方はFk+1 通りあり、(2)の(k+1)段までの上り方はFk+2 通りある。
従って、(k+2)段に上る方法は、
Fk+1 +Fk+2 =Fk+3
となり、n=k+2 の時も正しくなる。
自然数nを1と2の順序付きの和で表す方法の数
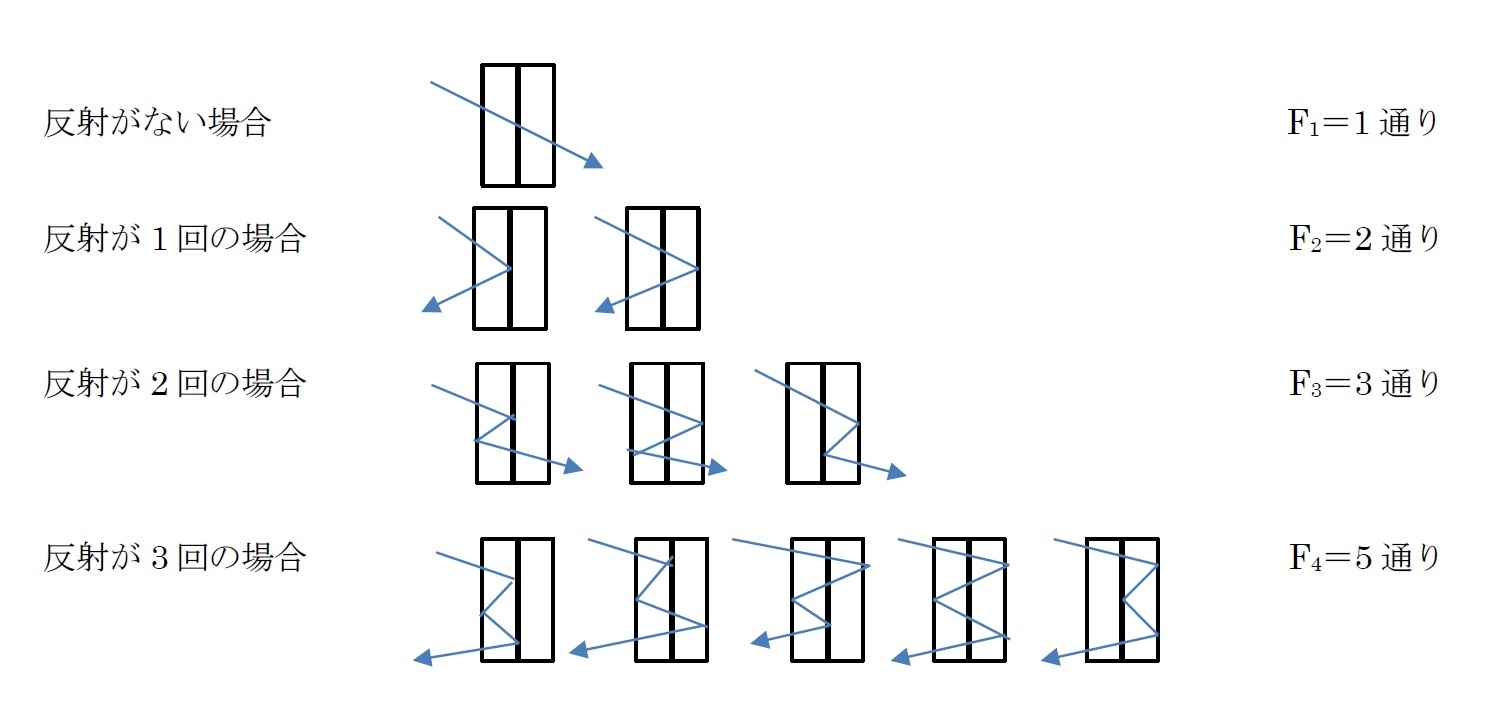
ガラス板を2枚重ねにした場合の光の反射の数
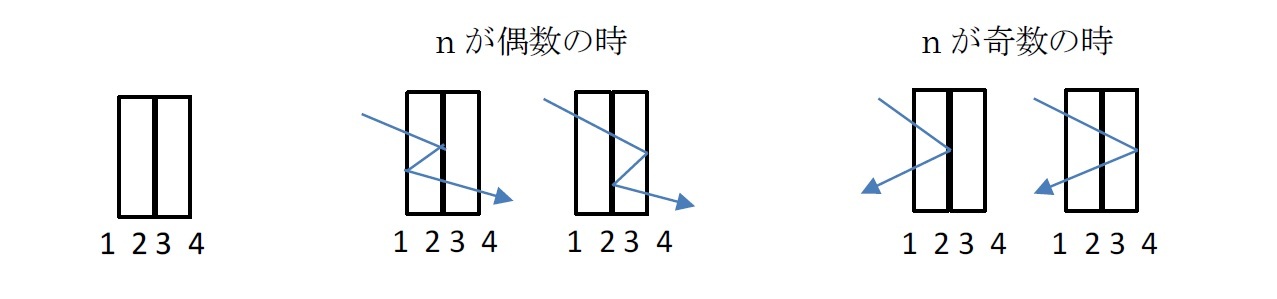
例えば、反射の回数nが偶数の時を考えると、最後の反射が反射面1で起こるなら、その前に(n-1)回の反射があり、最後の反射が反射面3で起こるなら、その直前の反射は反射面4で起きるしかなく、その前に(n-2)回の反射が起こっている。
従って、Fn+1=Fn+Fn-1 となり、Fnはフィボナッチ数列となっていることがわかる。
従って、Fn+1=Fn+Fn-1 となり、Fnはフィボナッチ数列となっていることがわかる。
株式投資におけるフィボナッチ数列の適用
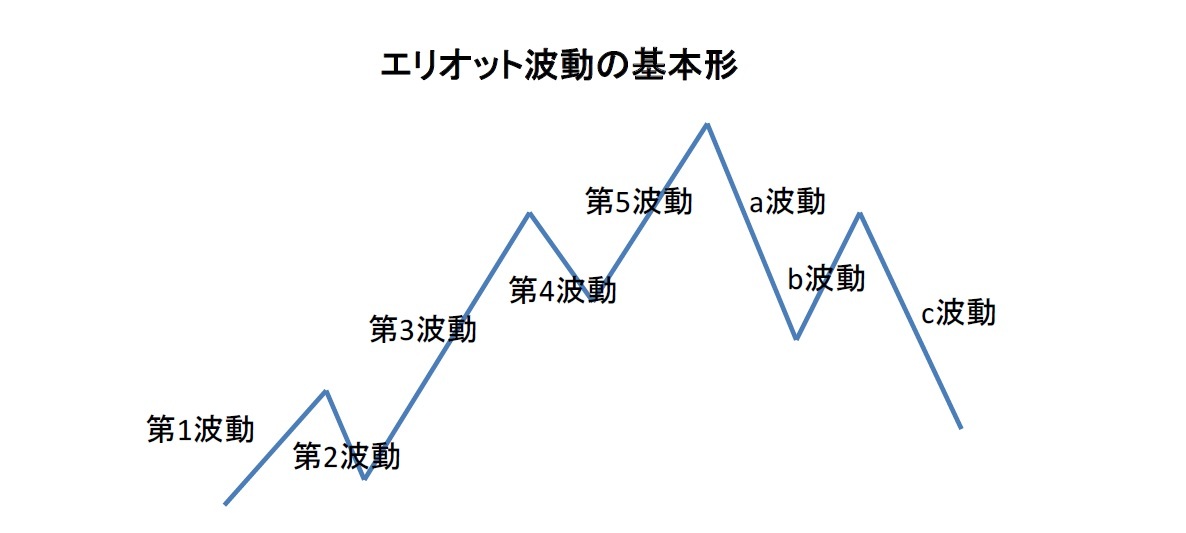
これが一般的に言われているものであるが、エリオットはさらに細かい波を分析していて、1つの相場サイクルは、5つの主要な波、21の中程度の波、89の細かい波から成る上昇局面と、3つの主要な波、13の中程度の波、55の細かい波から成る下降局面から、構成されるとした。ここで現れてくる「13」、「21」、「55」、「89」は全てフィボナッチ数となっている。
もう1つは、下げ相場に対する戻り幅の測定や上げ相場に対する上値目標値を、フィボナッチ数列や黄金比を用いて計算し、相場の予測値を出すものである。「フィボナッチ・リトレースメント(Fibonacci retracement)」と呼ばれて、チャート上の抵抗ラインと支持ラインの水準を示すテクニカル分析の一手法となっている。
具体的には、下図で示されるような感じである。即ち、株価が上昇や下落する際に、最大値や最小値から一定の水準に相当する株価が抵抗ラインや支持ラインとして意識され、この株価からいったんは反転や反落が想定されるというものである。具体的には、例えば、以下のような比率が主要なフィボナッチ比率として使用されている。
黄金比φ 0.618
φ2(=1-φ) 0.382
φ3 0.236
1-φ3 0.764
多くの投資家がこれらの水準を抵抗ラインや支持ラインとして意識している水準なので、この近辺には思惑の買いや売りが入りやすく出来高は必然的に大きくなっていくことになると言われている。
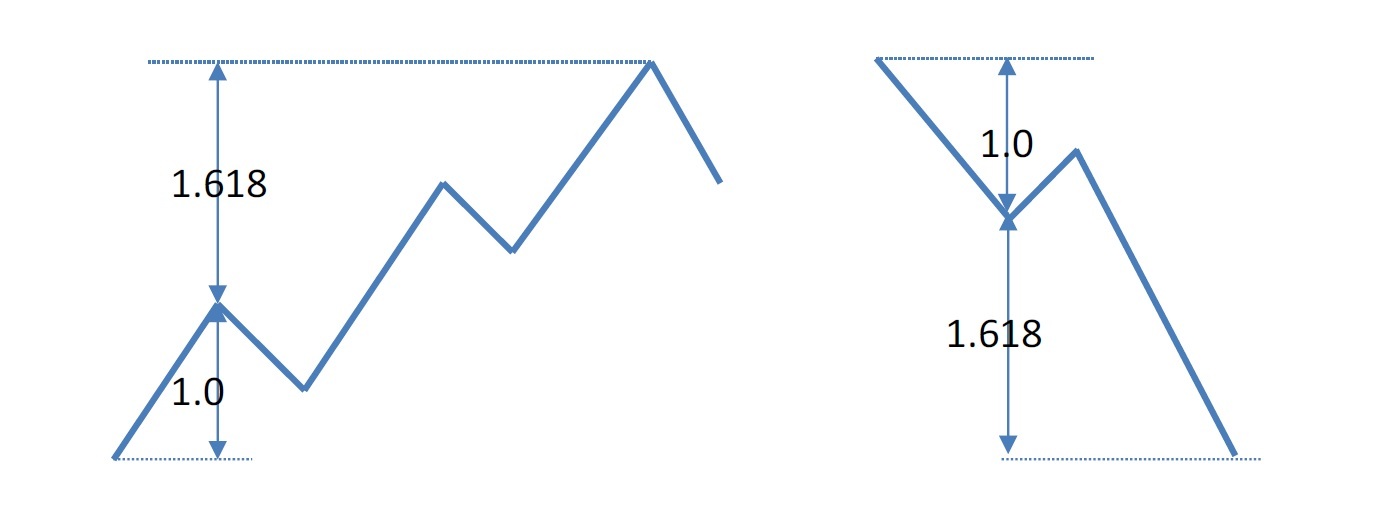
あるいは、エリオット波動との関係では、以下のような見方もされる。
もう1つは、下げ相場に対する戻り幅の測定や上げ相場に対する上値目標値を、フィボナッチ数列や黄金比を用いて計算し、相場の予測値を出すものである。「フィボナッチ・リトレースメント(Fibonacci retracement)」と呼ばれて、チャート上の抵抗ラインと支持ラインの水準を示すテクニカル分析の一手法となっている。
具体的には、下図で示されるような感じである。即ち、株価が上昇や下落する際に、最大値や最小値から一定の水準に相当する株価が抵抗ラインや支持ラインとして意識され、この株価からいったんは反転や反落が想定されるというものである。具体的には、例えば、以下のような比率が主要なフィボナッチ比率として使用されている。
黄金比φ 0.618
φ2(=1-φ) 0.382
φ3 0.236
1-φ3 0.764
多くの投資家がこれらの水準を抵抗ラインや支持ラインとして意識している水準なので、この近辺には思惑の買いや売りが入りやすく出来高は必然的に大きくなっていくことになると言われている。
あるいは、エリオット波動との関係では、以下のような見方もされる。
なお、株価水準を見る上では、半値戻しや3分の2、3分の1戻しといった考え方もある。従って、ここで紹介した黄金比やフィボナッチ数列を使用する考え方に基づく株式投資戦略が、本当に合理的で有効なものなのかどうかは保証されているわけではないので、あくまでも参考程度に考えていただきたい。
その他
フィボナッチ数列は、個体数の成長モデルや人口変動モデル、経済成長モデル等の研究に使用される。さらには、黄金比の時に述べたように、音楽や絵画、現代アート等の各種芸術作品、さらにはプログラミング・アルゴリズム等にも使用されている。
加えて、フランス人の数学者ブノワ・マンデルブロ(Benoît B. Mandelbrot)が考案した「フラクタル(fractal)」という概念にも関わっていくことになる。「フラクタル」というのは、自己相似性という特殊な性質を有する幾何学的図形のことをいい、図形の全体をいくつかの部分に分解していった時に同じ形が再現されていくことをいう。自然は一見すると無秩序なカオス状態のようにみえるが、よく観察すると同じ構造が繰り返されているような「フラクタル構造」になっている(ものが多く観察される)と言われている。「フラクタル」については、今後の研究員の眼で報告することとしたい。
カリフラワーの一種であるロマネスコは、明確なフラクタル図形をした野菜として有名で、そこで見られる螺旋が右向きで8本、左向きで13本等となって、フィボナッチ数列の数となっている。
加えて、フランス人の数学者ブノワ・マンデルブロ(Benoît B. Mandelbrot)が考案した「フラクタル(fractal)」という概念にも関わっていくことになる。「フラクタル」というのは、自己相似性という特殊な性質を有する幾何学的図形のことをいい、図形の全体をいくつかの部分に分解していった時に同じ形が再現されていくことをいう。自然は一見すると無秩序なカオス状態のようにみえるが、よく観察すると同じ構造が繰り返されているような「フラクタル構造」になっている(ものが多く観察される)と言われている。「フラクタル」については、今後の研究員の眼で報告することとしたい。
カリフラワーの一種であるロマネスコは、明確なフラクタル図形をした野菜として有名で、そこで見られる螺旋が右向きで8本、左向きで13本等となって、フィボナッチ数列の数となっている。
最後に
今回は、「フィボナッチ数列」について、3回に分けて報告してきた。フィボナッチ数列の性質の証明を見て、まさに高校時代のことを思い出された方もおられるのではないかと思われる。
今回の一連の研究員の眼を通じて、「フィボナッチ数列」を大学入試等のための勉強の対象としてみるのではなくて、改めて自然や社会の現象に観察される対象としてみた場合に、なかなか面白いものだと感じていただければと思っている。
今回の一連の研究員の眼を通じて、「フィボナッチ数列」を大学入試等のための勉強の対象としてみるのではなくて、改めて自然や社会の現象に観察される対象としてみた場合に、なかなか面白いものだと感じていただければと思っている。
(2021年03月26日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
| 2025/09/12 | 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月14日
今週のレポート・コラムまとめ【10/7-10/10発行分】 -
2025年10月10日
企業物価指数2025年9月~国内企業物価の上昇率は前年比2.7%、先行きは鈍化予想~ -
2025年10月10日
中期経済見通し(2025~2035年度) -
2025年10月10日
保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など -
2025年10月10日
若者消費の現在地(4)推し活が映し出す、複層的な消費の姿~データで読み解く20代の消費行動
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【フィボナッチ数列について(その3)-フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか(自然界以外)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
フィボナッチ数列について(その3)-フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか(自然界以外)-のレポート Topへ


















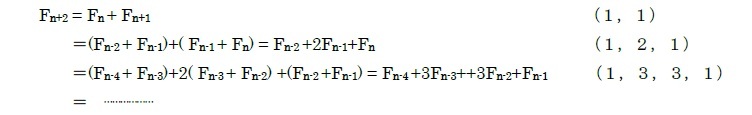



 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




