- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- フィボナッチ数列について(その2)-フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか(自然界)-
コラム
2021年02月26日
文字サイズ
- 小
- 中
- 大
はじめに
「フィボナッチ数列」について、前回の研究員の眼では、その定義や性質等について説明した。今回は、その「フィボナッチ数列」がどのようなところで使用され、どんな場面に現れてくるのかについて報告する。
フィボナッチ数列は、特に自然界の現象に数多く出現する。
その1つの例として、研究員の眼「黄金比φについて(その2)-黄金比はどこで使用され、どんな場面で現れてくるのか-」(2020.11.20)で、ひまわりの花における黄金螺旋の数は、フィボナッチ数列になっていることを紹介した。
今回の研究員の眼では、自然界に見られるフィボナッチ数列について報告する。
フィボナッチ数列は、特に自然界の現象に数多く出現する。
その1つの例として、研究員の眼「黄金比φについて(その2)-黄金比はどこで使用され、どんな場面で現れてくるのか-」(2020.11.20)で、ひまわりの花における黄金螺旋の数は、フィボナッチ数列になっていることを紹介した。
今回の研究員の眼では、自然界に見られるフィボナッチ数列について報告する。
葉序(植物の葉の付き方)
「葉序(ようじょ)(phyllotaxis)」というのは、植物の葉が茎に対して配列するときの様式をいう。この葉序は、主として以下の3つに分類される。
(1) 1つの節(茎に葉がついている部分)に葉が1枚ついている「互生葉序」
(2) 1つの節に2枚の葉をつける「対生葉序」
(3) 1つの節に3枚以上の葉を生じる「輪生葉序」
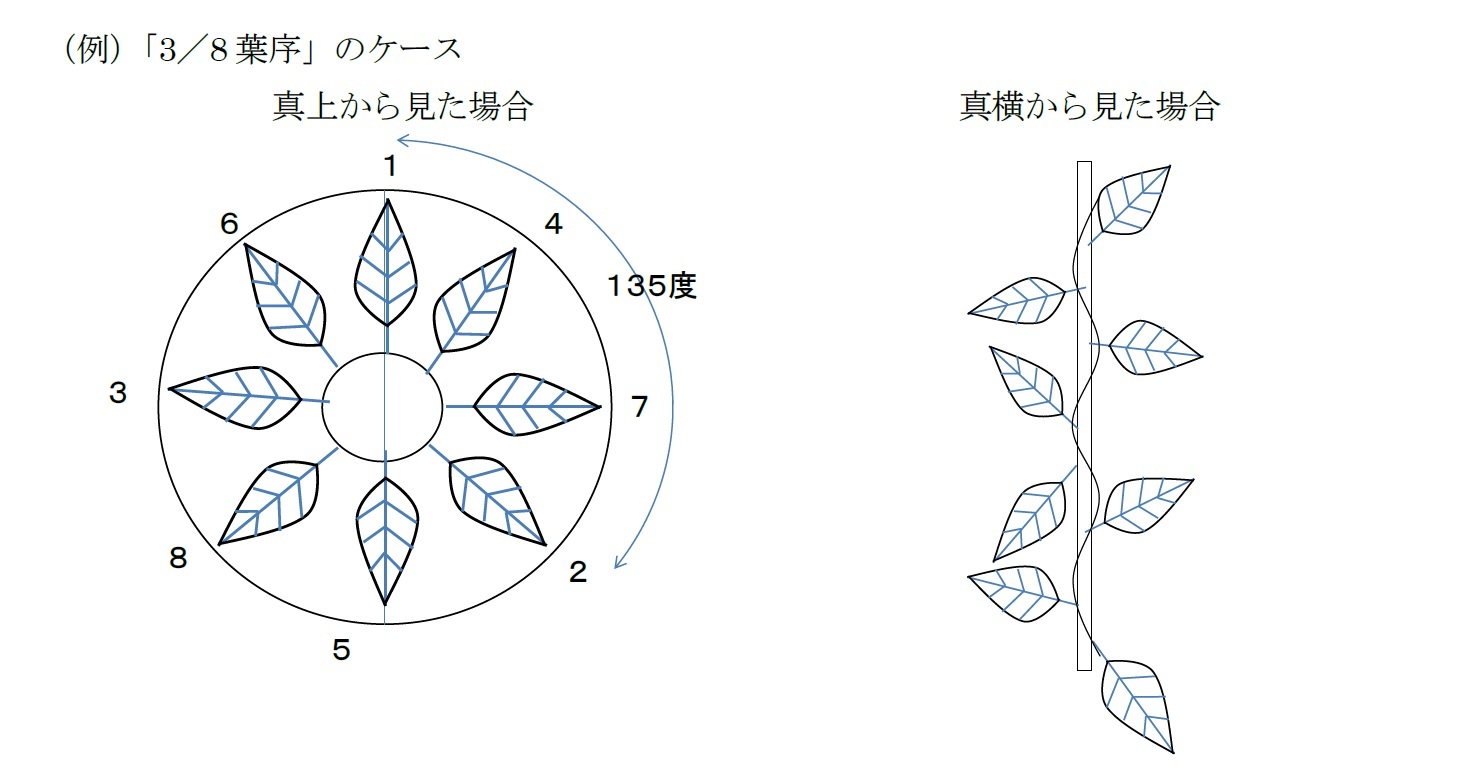
このうち、「互生葉序」は、多くの場合、茎の周りに螺旋状に葉をつけることから「螺旋葉序」とも呼ばれる。この「螺旋葉序」の場合、続いて発生した二つの葉を茎の軸の方向(真上又は真下)から見たときの二葉間の角度を「開度(かいど)」というが、この開度の違いから、いくつかの葉序のタイプが認められる。例えば、以下のようなものが挙げられる。
(1) 1つの節(茎に葉がついている部分)に葉が1枚ついている「互生葉序」
(2) 1つの節に2枚の葉をつける「対生葉序」
(3) 1つの節に3枚以上の葉を生じる「輪生葉序」
このうち、「互生葉序」は、多くの場合、茎の周りに螺旋状に葉をつけることから「螺旋葉序」とも呼ばれる。この「螺旋葉序」の場合、続いて発生した二つの葉を茎の軸の方向(真上又は真下)から見たときの二葉間の角度を「開度(かいど)」というが、この開度の違いから、いくつかの葉序のタイプが認められる。例えば、以下のようなものが挙げられる。
さらに、二葉間の角度である「開度」が、以前の研究員の眼「黄金比φについて(その1)-黄金比とはどのようなものなのか-」(2020.11.10)で説明した「黄金角(約137.5度)」1に近づいていくことを示した。上記の式において、n=2の場合がフィボナッチ数列によるものとなる。
なお、こうした葉序とフィボナッチ数列の関係に初めて気づいたのは、16世紀から17世紀にかけての有名な天文学者であるヨハネス・ケプラー(Johannes Kepler)であると言われている。彼は、樹木や葉に正五角形や五芒星が見られることに注目していたようだ。
1 「黄金角」は、360度を黄金比で分割した時の小さい部分の角度であり、360度÷φ2=137.5度、360度÷φ=222.5度となる。
1 「黄金角」は、360度を黄金比で分割した時の小さい部分の角度であり、360度÷φ2=137.5度、360度÷φ=222.5度となる。
螺旋の数―ひまわりの花、パイナップル、松かさ
植物の花や実に現れる螺旋の数もフィボナッチ数であることが多いと言われている。
ひまわりの花
こうすることで、円の内側に直線的に配列される場合に比べて、不要な空白の場所が節約できて、最も効率的に多くの種子を配列することができることになる。ただし、自然界でたびたび観測されるように、螺旋の数が多い場合には、中心から離れると螺旋の隙間にも種ができてしまい、途中から枝分かれしてフィボナッチ数にならないこともあるようだ。
パイナップルの表皮の斜列には、フィボナッチ数が現れている。表面を覆う六角形の鱗片は、左上から右下、右上から左下及びほぼ上から下への3種類の螺旋の一部となっており、この螺旋の数が、5本、8本、13本あるいは21本となっているようで、時計回りに13本、反時計回りに8本となっているのが通常のようだ。
同様に、松かさ(松ぼっくり)(pinecone)のかさの模様においても、右巻きと左巻きのらせんがあり、その数は。5本、8本。13本といったフィボナッチ数となっている。なお、英語の「pineapple」は、本来は「松の果実」ということで、松かさのことであったが、後に松かさに似た別の果物である現在のパイナップルを指すようになっている。
サボテンの刺座
サボテンは刺座(アレオーレ)と呼ばれる特殊な短枝を持つ。あの刺の付け根にある綿毛のようなもののことをいう。短枝自体は極端に短縮し脇芽と殆ど同化した枝となっている。
この刺座は螺旋構造を成し、その数は8本、13本、21本というようなフィボナッチ数となっている。
同様に、松かさ(松ぼっくり)(pinecone)のかさの模様においても、右巻きと左巻きのらせんがあり、その数は。5本、8本。13本といったフィボナッチ数となっている。なお、英語の「pineapple」は、本来は「松の果実」ということで、松かさのことであったが、後に松かさに似た別の果物である現在のパイナップルを指すようになっている。
サボテンの刺座
サボテンは刺座(アレオーレ)と呼ばれる特殊な短枝を持つ。あの刺の付け根にある綿毛のようなもののことをいう。短枝自体は極端に短縮し脇芽と殆ど同化した枝となっている。
この刺座は螺旋構造を成し、その数は8本、13本、21本というようなフィボナッチ数となっている。
花びらの数
ハチやアリ等の祖先の数
これまで植物における例を挙げてきたが、動物においてもフィボナッチ数列が現れる。
例えば、ハチやアリなど、雄に父親がない家系を辿って、その祖先の数を数えると、フィボナッチ数列となる。具体的には、親(父母)2匹に対して、祖父母3匹、曽祖父母5匹、高祖父母8匹…となっていく。n世代前ならFn=Fn-1+Fn-2(n≧3)匹となる。
人間の場合、当然のことながら、一人の人間に対して2人の両親が存在することから、各世代の祖先の数は2のべき乗になっており、n世代前であれば2nとなる。
ところが、例えばミツバチの場合、「半倍数性(Haplodiploidy)」と呼ばれる遺伝形式を有していて、母親が産卵時に交尾をしていたら、その子供は必ず雌になるのに対して、母親が産卵時に交尾をしていなくて生まれてくる子供は必ず雄になる(即ち、受精卵からの子供は雌で、未受精卵からの子供は雄になる)ことにより、雄は父親がいないことになる。
n世代前の祖先の数をFnとする場合、その1つ前の(n+1)世代の祖先の数は、雌にだけ父親がいることから、
Fn+1=Fn(雄)+2Fn(雌)= Fn(雄)+Fn(雌)+Fn(雌)=Fn+Fn(雌)
ここで、n世代の雌の数Fn(雌)は、(n-1)世代が必ず母親を有することから、Fn-1に等しくなる。よって、
Fn+1=Fn+Fn-1
となって、フィボナッチの漸化式が満たされることになる。
このことは、また各世代の雌雄比(=雌/雄)が黄金比φ(≒1.618)に収束していくことを示している。ただし、これはあくまでも数学的モデルによる各世代における雌雄比に関する結論であって、実際には働きバチは殆どが雌で、実際の雌雄比はもっと高い(雌が圧倒的に多い)とも言われているようである。
例えば、ハチやアリなど、雄に父親がない家系を辿って、その祖先の数を数えると、フィボナッチ数列となる。具体的には、親(父母)2匹に対して、祖父母3匹、曽祖父母5匹、高祖父母8匹…となっていく。n世代前ならFn=Fn-1+Fn-2(n≧3)匹となる。
人間の場合、当然のことながら、一人の人間に対して2人の両親が存在することから、各世代の祖先の数は2のべき乗になっており、n世代前であれば2nとなる。
ところが、例えばミツバチの場合、「半倍数性(Haplodiploidy)」と呼ばれる遺伝形式を有していて、母親が産卵時に交尾をしていたら、その子供は必ず雌になるのに対して、母親が産卵時に交尾をしていなくて生まれてくる子供は必ず雄になる(即ち、受精卵からの子供は雌で、未受精卵からの子供は雄になる)ことにより、雄は父親がいないことになる。
n世代前の祖先の数をFnとする場合、その1つ前の(n+1)世代の祖先の数は、雌にだけ父親がいることから、
Fn+1=Fn(雄)+2Fn(雌)= Fn(雄)+Fn(雌)+Fn(雌)=Fn+Fn(雌)
ここで、n世代の雌の数Fn(雌)は、(n-1)世代が必ず母親を有することから、Fn-1に等しくなる。よって、
Fn+1=Fn+Fn-1
となって、フィボナッチの漸化式が満たされることになる。
このことは、また各世代の雌雄比(=雌/雄)が黄金比φ(≒1.618)に収束していくことを示している。ただし、これはあくまでも数学的モデルによる各世代における雌雄比に関する結論であって、実際には働きバチは殆どが雌で、実際の雌雄比はもっと高い(雌が圧倒的に多い)とも言われているようである。
その他の例
こうした我々が目にすることができる動植物だけでなく、その他の自然界にもフィボナッチ数列との関係を見て取ることができる。
それは、今回の研究員の眼では紹介していないが、顕微鏡でしかみることができないウイルスの世界から、巨大な銀河の世界にまで至っているようだ。
それは、今回の研究員の眼では紹介していないが、顕微鏡でしかみることができないウイルスの世界から、巨大な銀河の世界にまで至っているようだ。
最後に
今回は、自然界に出現しているフィボナッチ数列の例を挙げてきた。
なぜ、このようにフィボナッチ数列が現れてくるのだろうか。
これについては、研究員の眼「黄金比φについて(その1)」(2020.11.10)で説明したように、黄金比φの連分数表示が
なぜ、このようにフィボナッチ数列が現れてくるのだろうか。
これについては、研究員の眼「黄金比φについて(その1)」(2020.11.10)で説明したように、黄金比φの連分数表示が
というように、(他の数では見られない)「1」のみが連続する形の偏りのないものとなっていること、そのため、この黄金比に基づく黄金角で葉や花びら等が配置されていくことが最も重なりがなく効率的なものとなっていること、そしてフィボナッチ数列の隣接するフィボナッチ数の比が黄金比φに収束していくこと、等がその背景にあるようである。
自然界の中にみられる黄金比や黄金角やフィボナッチ数列が、自然に備わっていたものなのか、あるいは長い進化の歴史を経て現在の形になっているのかはよくわからないが、いずれにしても、最も優位で適切なものであるからこそ、現在まで生き残ってきたということになるのだろう。
今後、どなたかとヒマワリの花を見たり、どなたかにバラの花を贈るような機会があったら、黄金比やフィボナッチ数列のことを思い出して、講釈をされてみるのもよいかもしれない。最も相手がどのような反応をするかはわからないので、その点はお気を付けいただきたい。
自然界の中にみられる黄金比や黄金角やフィボナッチ数列が、自然に備わっていたものなのか、あるいは長い進化の歴史を経て現在の形になっているのかはよくわからないが、いずれにしても、最も優位で適切なものであるからこそ、現在まで生き残ってきたということになるのだろう。
今後、どなたかとヒマワリの花を見たり、どなたかにバラの花を贈るような機会があったら、黄金比やフィボナッチ数列のことを思い出して、講釈をされてみるのもよいかもしれない。最も相手がどのような反応をするかはわからないので、その点はお気を付けいただきたい。
(2021年02月26日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月23日
中国:25年7~9月期GDPの評価-秋風索莫の気配が漂う中国経済。内需の悪化により成長率は減速 -
2025年10月23日
パワーカップルと小学校受験-データで読み解く暮らしの風景 -
2025年10月22日
高市新政権が発足、円相場の行方を考える~マーケット・カルテ11月号 -
2025年10月22日
貿易統計25年9月-米国向け自動車輸出が数量ベースで一段と落ち込む。7-9月期の外需寄与度は前期比▲0.4%程度のマイナスに -
2025年10月22日
米連邦地裁、Googleへの是正措置を公表~一般検索サービス市場における独占排除
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【フィボナッチ数列について(その2)-フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか(自然界)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
フィボナッチ数列について(その2)-フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか(自然界)-のレポート Topへ



















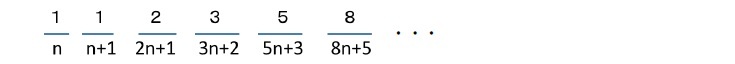






 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




