- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 曲線にはどんな種類があって、どう社会に役立っているのか(その1)-円錐曲線(楕円、放物線、双曲線)とは-
コラム
2023年10月16日
文字サイズ
- 小
- 中
- 大
はじめに
学生時代に、複雑な算式を図表で表すと、いろんな形の曲線が描かれるのを勉強したと思う。この時には、「へー、そうなんだ」ぐらいの認識でおられた方も多く、むしろ、こうした算式の取扱いに四苦八苦して、結果として得られている曲線が、社会において、あるいは自然界において、どのような形で現れていて、どう役立っているのか、については、あまり説明がなく、殆ど勉強する機会もなかったのではないかと思われる。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告してみたい。まずは、今回は、楕円、放物線、双曲線等の「円錐曲線」について、その定義等について説明する。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告してみたい。まずは、今回は、楕円、放物線、双曲線等の「円錐曲線」について、その定義等について説明する。
円錐曲線とは
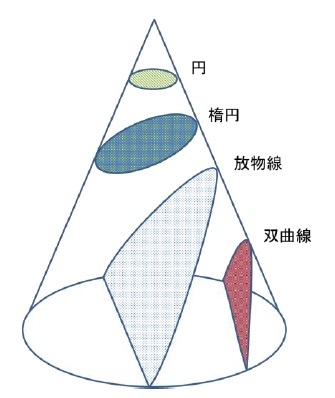
「円錐曲線(conic curve、conic section)」というのは、円錐面を任意の平面で切断したときの断面としてえられる曲線群の総称、を指している。具体的には、以下の図のように、円錐をどのような平面で切断するのかによって、切断面は「円(circle)」や「楕円(ellipse)」、「放物線(parabola)」、「双曲線(hyperbola)」になる1。
具体的には、円錐を頂点を通らない平面で切断する場合に、以下の通りとなる。
具体的には、円錐を頂点を通らない平面で切断する場合に、以下の通りとなる。
(3) 放物線(母線に平行な面で切断)
x2=4ay 又は y2=4ax
x2=4ay 又は y2=4ax
又は、これらを「固有二次曲線」という。なお、先の2次式(※)で表される図形には、固有二次曲線に加えて、「退化した二次曲線」と呼ばれる、二直線(軸を全て含む平面で切断)、一直線、1点、さらには実数の範囲には解が無い「虚円、虚楕円」がある。
上記の2次式(※)との関係では、P=AC-B2/4 としたとき、基本的に以下の通りとなる。
P>0 のとき 楕円
P=0 のとき 放物線
P<0 のとき 双曲線
2 このように、円錐曲線を二次曲線として表現する方式は、「我思う、ゆえに我あり」で有名なフランスの哲学者かつ数学者であるㇽネ・デカルト(René Descartes)が、2つの実数によって平面上の点の位置(座標)を表す「デカルト座標」を発明したことによるもので、これにより「解析幾何学」の発展の基礎が築かれた。また、二次曲線については、無限大の記号∞を導入したことでも有名なイングランドの数学者であるジョン・ウォリス(John Wallis)が、1655年に、円錐曲線を初めて二次曲線として定義して解析する論文を発表している。
3 曲線には、シッソイド,ストロフォイド等の三次曲線やパスカルの蝸牛線(リマソン)等の四次曲線等のさらなる高次曲線がある。これらについては、別途報告することとする。
4 生成曲線とも呼ばれ、それが定められた経路をたどって動く時の軌跡として新しい図形を生成する曲線。円錐の場合、展開した場合の扇形の部分であり、円錐の頂点から側面上に底面に向かって真っすぐに引かれる線となる。
上記の2次式(※)との関係では、P=AC-B2/4 としたとき、基本的に以下の通りとなる。
P>0 のとき 楕円
P=0 のとき 放物線
P<0 のとき 双曲線
2 このように、円錐曲線を二次曲線として表現する方式は、「我思う、ゆえに我あり」で有名なフランスの哲学者かつ数学者であるㇽネ・デカルト(René Descartes)が、2つの実数によって平面上の点の位置(座標)を表す「デカルト座標」を発明したことによるもので、これにより「解析幾何学」の発展の基礎が築かれた。また、二次曲線については、無限大の記号∞を導入したことでも有名なイングランドの数学者であるジョン・ウォリス(John Wallis)が、1655年に、円錐曲線を初めて二次曲線として定義して解析する論文を発表している。
3 曲線には、シッソイド,ストロフォイド等の三次曲線やパスカルの蝸牛線(リマソン)等の四次曲線等のさらなる高次曲線がある。これらについては、別途報告することとする。
4 生成曲線とも呼ばれ、それが定められた経路をたどって動く時の軌跡として新しい図形を生成する曲線。円錐の場合、展開した場合の扇形の部分であり、円錐の頂点から側面上に底面に向かって真っすぐに引かれる線となる。
円錐曲線の離心率による定義
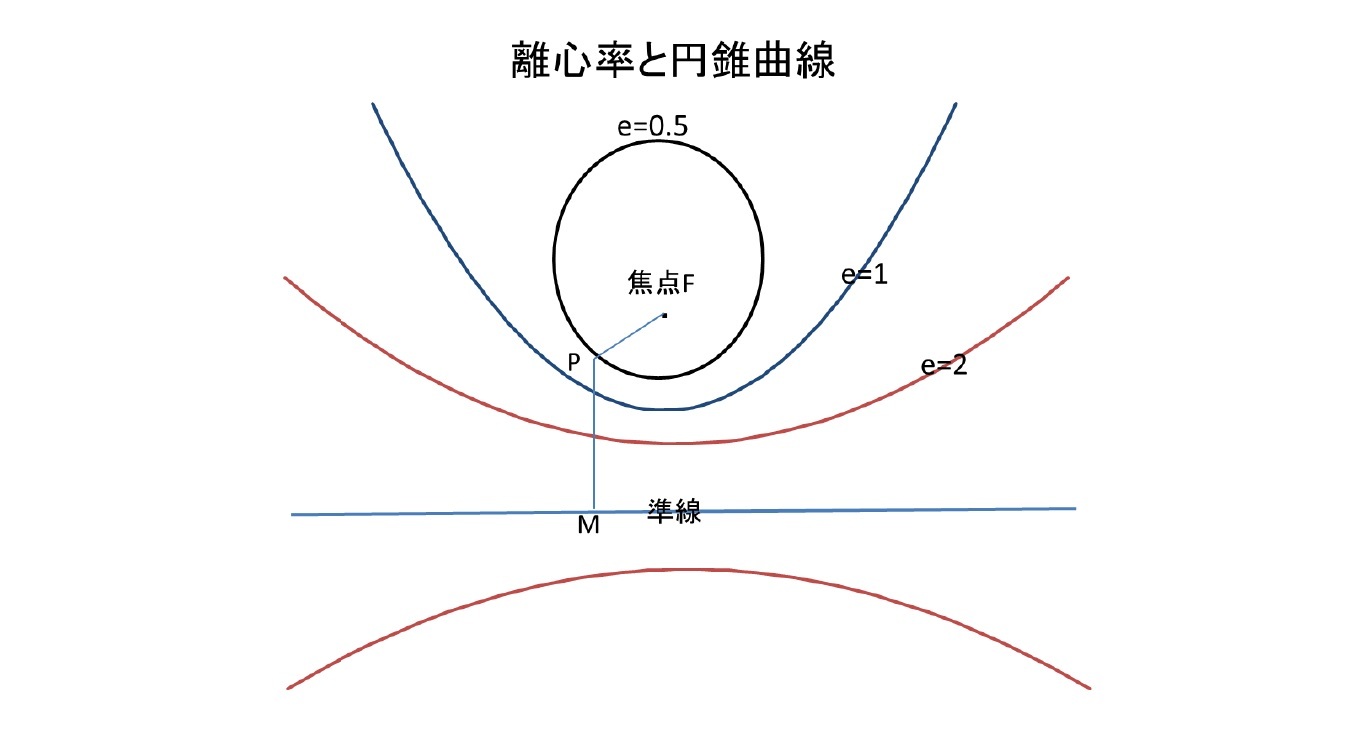
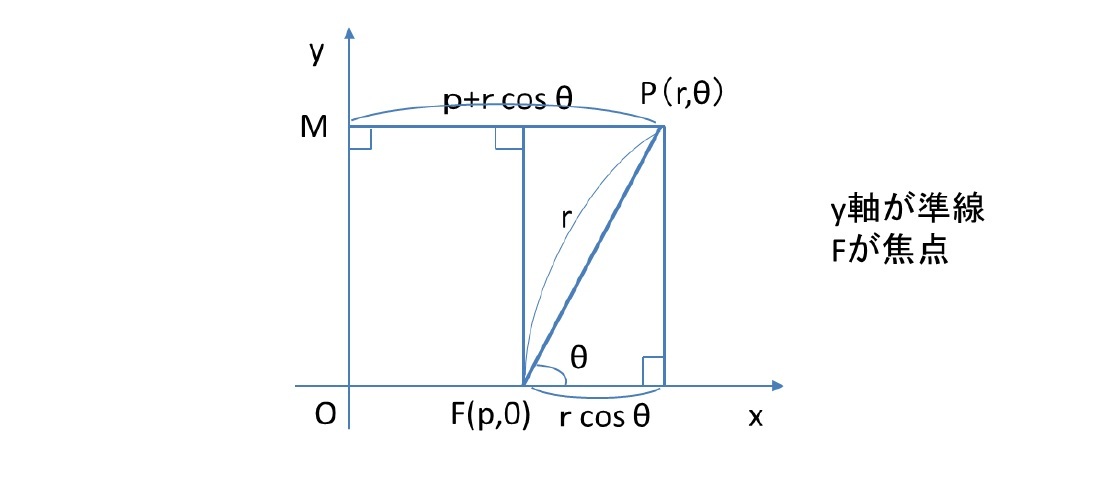
直線と、その直線上に含まれないような点Fを取り、点Fから直線への垂線に対して点Fのある方向が正と定め、それをx軸とする。直線上で点Mを動かすとき、その直角位置上で FP : PM= e : 1(e > 0)を満たすような点Pの集合は円錐曲線を描く。この時、FPとPMの比の値eを「離心率(eccentricity)」といい、直線を「準線(directrix)」、点Fを「焦点(focus)」という5。円錐曲線は、焦点、準線、離心率の3要素を与えることで作図できる。その定義から、円錐曲線上の点は、どこを取っても準線までの距離と焦点までの距離が同じ比率eになる。
具体的には、離心率 eによって、描かれる円錐曲線は、以下の通りとなる。
0 < e < 1 のとき 楕円
e = 1 のとき 放物線
e > 1 のとき 双曲線
なお、e=0 の時が「円」に相当することになるが、実際にはこの時には「点」になる。
即ち、離心率が1より小さい間は閉曲線になるが、離心率が1になると閉曲線でなくなり、さらに離心率が1より大きくなると曲線は大きく拡がっていくことになる。
離心率は円錐曲線の形状を決める唯一のパラメーターで、離心率が同じであれば、必ず同じ形状(相似)になる。相似とは、拡大縮小、平行移動、回転等の操作を組み合わせることで、一方の図形が他方とぴったり重なることをいう。
「円」については、すべての円が相似であることは形状的に明らかだが、「楕円」については、その離心率は扁平率6に対応しており、扁平率が同じ楕円は相似となる。離心率あるいは扁平率が0に近いほど円に近く、1に近いほど潰れた楕円になる。
「放物線」については、離心率が1に固定されていることから、あらゆる放物線は相似となる(なお、縦横比の異なる拡大縮小は相似の操作として認められていないが、縦横比を変更しても、放物線は放物線となる)。
「双曲線」の離心率は2本の漸近線のなす角と対応しており、角度さえ同じであれば、相似になる。例えば、全ての直角双曲線(漸近線のなす角度が90%の双曲線)は離心率が√2となり、互いに相似となる。なお、離心率が1に近いほど頂点の鋭い曲線になり、値が大きいほど緩やかな曲線になる。因みに、離心率が無限大に近づくほど準線と一致する直線状になっていく。
具体的には、離心率 eによって、描かれる円錐曲線は、以下の通りとなる。
0 < e < 1 のとき 楕円
e = 1 のとき 放物線
e > 1 のとき 双曲線
なお、e=0 の時が「円」に相当することになるが、実際にはこの時には「点」になる。
即ち、離心率が1より小さい間は閉曲線になるが、離心率が1になると閉曲線でなくなり、さらに離心率が1より大きくなると曲線は大きく拡がっていくことになる。
離心率は円錐曲線の形状を決める唯一のパラメーターで、離心率が同じであれば、必ず同じ形状(相似)になる。相似とは、拡大縮小、平行移動、回転等の操作を組み合わせることで、一方の図形が他方とぴったり重なることをいう。
「円」については、すべての円が相似であることは形状的に明らかだが、「楕円」については、その離心率は扁平率6に対応しており、扁平率が同じ楕円は相似となる。離心率あるいは扁平率が0に近いほど円に近く、1に近いほど潰れた楕円になる。
「放物線」については、離心率が1に固定されていることから、あらゆる放物線は相似となる(なお、縦横比の異なる拡大縮小は相似の操作として認められていないが、縦横比を変更しても、放物線は放物線となる)。
「双曲線」の離心率は2本の漸近線のなす角と対応しており、角度さえ同じであれば、相似になる。例えば、全ての直角双曲線(漸近線のなす角度が90%の双曲線)は離心率が√2となり、互いに相似となる。なお、離心率が1に近いほど頂点の鋭い曲線になり、値が大きいほど緩やかな曲線になる。因みに、離心率が無限大に近づくほど準線と一致する直線状になっていく。
この時、先に述べた時と同様に、以下の通りとなる。
0 < e < 1 のとき 楕円
e = 1 のとき 放物線
e > 1 のとき 双曲線
5 「準線(directrix)」や「焦点(focus)」の用語は、次回の研究員の眼で説明する、有名な惑星の運動法則である「ケプラーの法則」を発見したケプラーによって導入されている。
6 楕円が円に比べて、どれだけ扁平か(潰れているか)を表す値で、長半径をa、短半径をbとした時に、1-b/a で定義される値である。
0 < e < 1 のとき 楕円
e = 1 のとき 放物線
e > 1 のとき 双曲線
5 「準線(directrix)」や「焦点(focus)」の用語は、次回の研究員の眼で説明する、有名な惑星の運動法則である「ケプラーの法則」を発見したケプラーによって導入されている。
6 楕円が円に比べて、どれだけ扁平か(潰れているか)を表す値で、長半径をa、短半径をbとした時に、1-b/a で定義される値である。
(2023年10月16日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる -
2025年10月24日
企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年10月24日
消費者物価(全国25年9月)-コアCPI上昇率は拡大したが、先行きは鈍化へ -
2025年10月24日
保険業界が注目する“やせ薬”?-GLP-1は死亡率改善効果をもたらすのか -
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1)
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【曲線にはどんな種類があって、どう社会に役立っているのか(その1)-円錐曲線(楕円、放物線、双曲線)とは-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
曲線にはどんな種類があって、どう社会に役立っているのか(その1)-円錐曲線(楕円、放物線、双曲線)とは-のレポート Topへ


















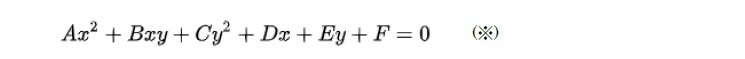



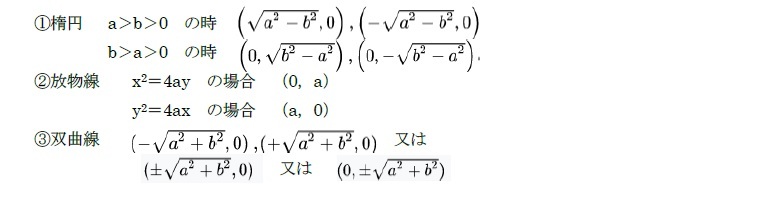


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




