- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 図形数について(その2)-3次元立体図形に関する図形数、ウェアリングの問題等-
コラム
2022年12月28日
文字サイズ
- 小
- 中
- 大
はじめに
図形数に関する前回の研究員の眼では、「図形数(figurate number)」と呼ばれるもののうちの、2次元の平面図形に関する数について紹介した。
今回は、三角錐数や立方数等の3次元の立体図形に関する図形数、パスカルの三角形及びウェアリングの問題について紹介することにする。
今回は、三角錐数や立方数等の3次元の立体図形に関する図形数、パスカルの三角形及びウェアリングの問題について紹介することにする。
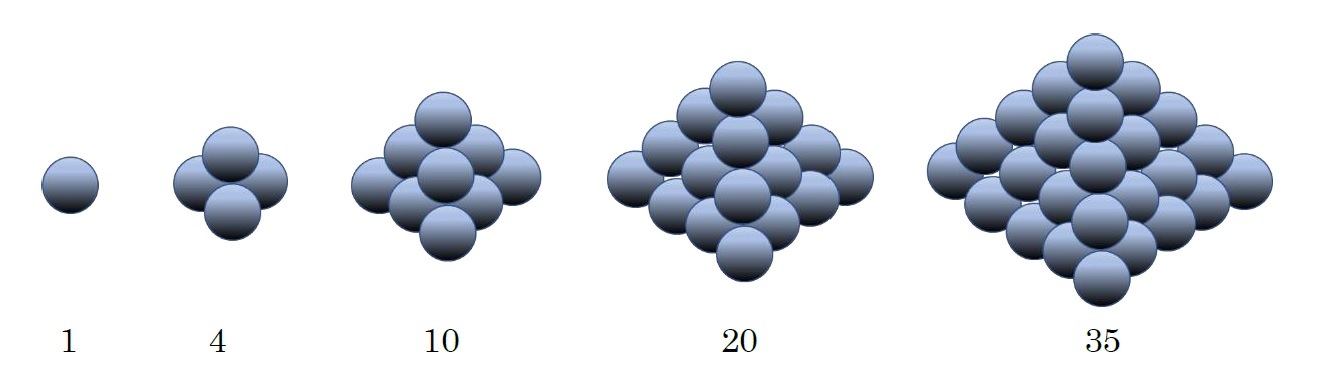
三角錐数(正四面体数)
となる。これはまた、組み合わせの記号を使うと、Tn=n+2C3 となる。
三角錐数(正四面体数)の性質
三角錐数は「奇数-偶数-偶数-偶数」といった順番の繰り返しで現れる。
実際に、1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816,… というような具合である。
実際に、1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816,… というような具合である。
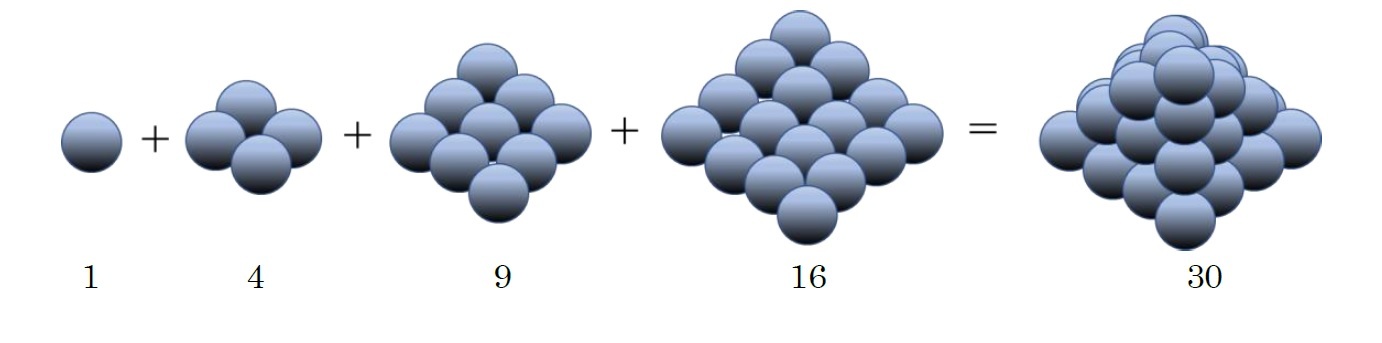
立方数(正六面体数)
この式が正しいことは、数学的帰納法で証明される。
即ち、「1からn 番目の立方数 n3 までの和は、1からnまでの和の二乗」となる。
なお、この算式については、以下のアプローチからも得られる。即ち、
13=1
23=3+5
33=7+9+11
43=13+15+17+19
53=21+23+25+27+29
・・・・・・
k3=(k2-(k-1))+(k2-(k-1)+2)+・・・+(k2-1)
+(k2+1)+・・・+(k2+(k-1)-2)+(k2+(k-1)) kが偶数の時
=(k2-(k-1))+(k2-(k-1)+2)+・・・+(k2-2)+k2+
+(k2+2)+・・・+(k2+(k-1)-2)+(k2+(k-1)) kが奇数の時
とk3は連続する奇数のみで表される。ここで、
(k-1)2+((k-1)-1)=k2―k-1(=(k2-(k-1))-2 )
となることから、1からn 番目の立方数 n3 までの和は、1からn2+(n-1)までの全ての奇数の合計値となる。即ち、以下の式が成り立つことになる。
即ち、「1からn 番目の立方数 n3 までの和は、1からnまでの和の二乗」となる。
なお、この算式については、以下のアプローチからも得られる。即ち、
13=1
23=3+5
33=7+9+11
43=13+15+17+19
53=21+23+25+27+29
・・・・・・
k3=(k2-(k-1))+(k2-(k-1)+2)+・・・+(k2-1)
+(k2+1)+・・・+(k2+(k-1)-2)+(k2+(k-1)) kが偶数の時
=(k2-(k-1))+(k2-(k-1)+2)+・・・+(k2-2)+k2+
+(k2+2)+・・・+(k2+(k-1)-2)+(k2+(k-1)) kが奇数の時
とk3は連続する奇数のみで表される。ここで、
(k-1)2+((k-1)-1)=k2―k-1(=(k2-(k-1))-2 )
となることから、1からn 番目の立方数 n3 までの和は、1からn2+(n-1)までの全ての奇数の合計値となる。即ち、以下の式が成り立つことになる。
前回の研究員の眼の四角数で説明したように、この奇数の和は四角数を構成していることから、
立方数(正六面体数)の性質
立方数にも、いくつかの性質がある。
・2通りの方法で、2つの立方数の和として表される最小の自然数は、1729 = 123 + 13 = 103 + 93 である。これについては、以前の研究員の眼「天才数学者ラマヌジャン-「奇蹟がくれた数式」を観て-」(2017.3.21)において、「タクシー数」ということで紹介した。
・全ての自然数は、9個以下の立方数の和として表される(ウェアリングの問題)。これについては、後述する。
・立方数を2つの立方数の和として表すことはできない。これは、有名な「フェルマーの最終定理」(3 以上の自然数 n について、xn + yn = zn となる自然数の組 (x, y, z) は存在しない)におけるn=3 のケースに該当している。
・2通りの方法で、2つの立方数の和として表される最小の自然数は、1729 = 123 + 13 = 103 + 93 である。これについては、以前の研究員の眼「天才数学者ラマヌジャン-「奇蹟がくれた数式」を観て-」(2017.3.21)において、「タクシー数」ということで紹介した。
・全ての自然数は、9個以下の立方数の和として表される(ウェアリングの問題)。これについては、後述する。
・立方数を2つの立方数の和として表すことはできない。これは、有名な「フェルマーの最終定理」(3 以上の自然数 n について、xn + yn = zn となる自然数の組 (x, y, z) は存在しない)におけるn=3 のケースに該当している。
四角錘数
となる。
四角錘数の性質
四角錐数にも、いくつかの性質がある。
・四角錐数は「奇数-奇数-偶数-偶数」といった順番の繰り返しで現れる。
実際に、1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650,… というような具合である。
・四角錐数のうち三角数でもある数は 1, 55, 91, 208335 の4つのみ
・四角錐数のうち四角数(平方数)でもある数は 1 と 4900(24番目の四角錐数)の2つのみ
・四角錐数かつ三角錐数でもある数は 1 のみ
・四角錘数は2つの連続する三角錐数の和となる(因みに、前回の研究員の眼で述べたように「四角数は2つの連続する三角数の和」となっている)
これは、上式から Sn=n+1C3+n+2C3 となっていることで示せる。
・n×nマスの方眼の中に含まれる正方形の数は n 番目の四角錐数Snに等しくなる。
これは、四角錘数の構成要素を考えれてみれば確認できる。
・四角錐数は「奇数-奇数-偶数-偶数」といった順番の繰り返しで現れる。
実際に、1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650,… というような具合である。
・四角錐数のうち三角数でもある数は 1, 55, 91, 208335 の4つのみ
・四角錐数のうち四角数(平方数)でもある数は 1 と 4900(24番目の四角錐数)の2つのみ
・四角錐数かつ三角錐数でもある数は 1 のみ
・四角錘数は2つの連続する三角錐数の和となる(因みに、前回の研究員の眼で述べたように「四角数は2つの連続する三角数の和」となっている)
これは、上式から Sn=n+1C3+n+2C3 となっていることで示せる。
・n×nマスの方眼の中に含まれる正方形の数は n 番目の四角錐数Snに等しくなる。
これは、四角錘数の構成要素を考えれてみれば確認できる。
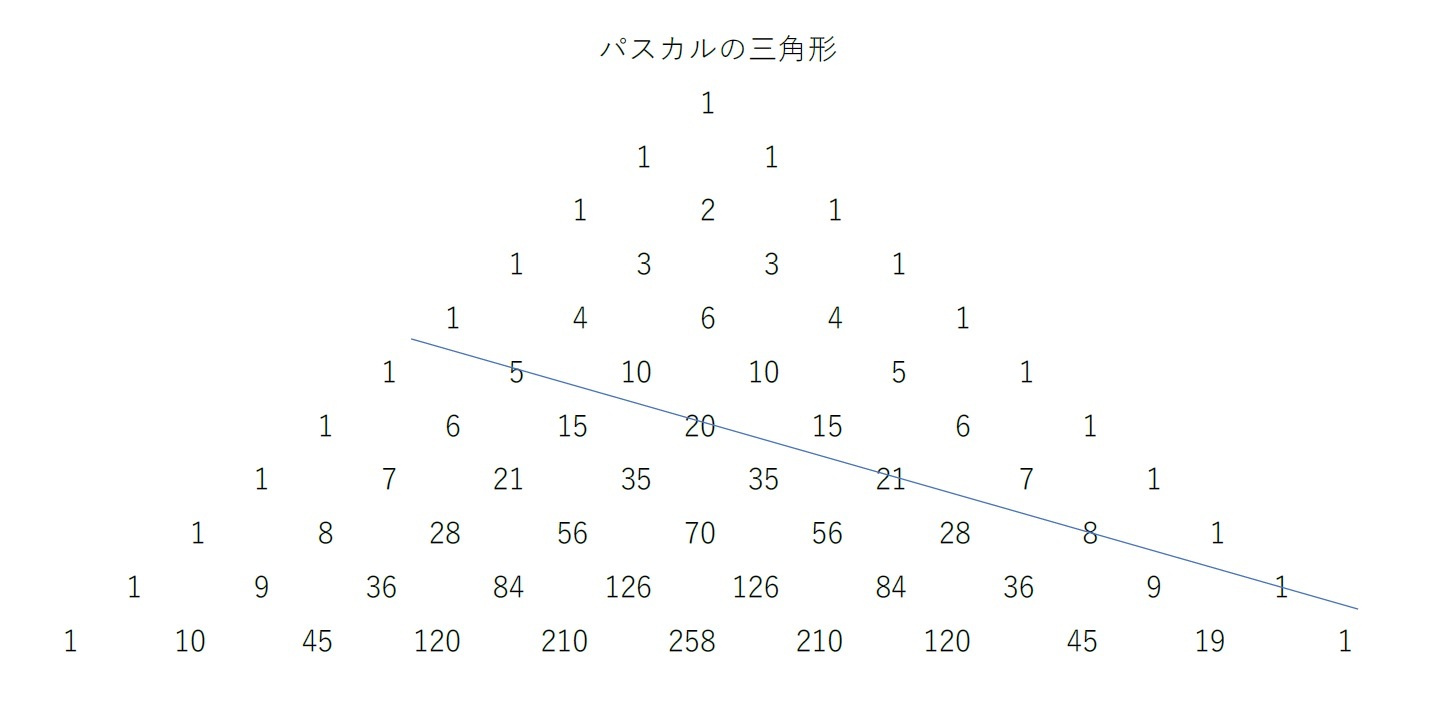
パスカルの三角形
パスカルの三角形については、以前の研究員の眼「フィボナッチ数列について(その3)-フィボナッチ数列はどこで使用され、どんな場面に現れてくるのか(自然界以外)-」(2021.3.26)で紹介した。そこで説明したように、このパスカルの三角形において、桂馬跳びの様に斜め方向に数字を拾い、その合計を取っていくと「フィボナッチ数列」が現れる。例えば、上の図の上から6段目の斜め線で示している数値の合計は5+20+21+8+1=55 はフィボナッチ数になっているというような具合である。
一方で、よりシンプルに、パスカルの三角形における数列を左上(または右上)にある列から順にみてみると、以下の通り、これまで紹介してきた図形数等の数列になっている。
単数列 1, 1, 1, 1, 1, 1, 1, 1, 1,…,
自然数の数列 1, 2, 3, 4, 5, 6, 7, 8, 9,…,
三角数の数列 1, 3, 6, 10, 15, 21, 28, 36, 45,…,
三角錐数(正四面体数)の数列 1, 4, 10, 20, 35, 56, 84, 120, 165,…,
因みに、その次の数列 1, 5, 15, 35, 70, 126, 210, 330, 495, …, については、「五胞体数」と呼ばれる数列になっている。「五胞体(ごほうたい)」と呼ばれるのは、4次元単体で、5つの胞で囲まれたものであり、全ての胞が四面体、全ての面が三角形となっているものである。いわば「4次元四面体」に相当し、その意味では「五胞体数」は「4次元正面体数」(「4次元超四面体」とも呼ばれる)に相当するものになっている。同様に、その次の数列 1,6,21,56,126,252,462.792,…, については、「六胞体数」と呼ばれる数列で、「5次元四面体数」(「5次元超々四面体数」)と呼べるものになっている。
なお、パスカルの三角形の横の数列は、当然に2項展開の各項の係数を示しているが、その各行の合計値は2のべき乗(n行目の場合 2n-1)となっている。
1 なお、このような数字の三角形については、パスカルよりも遥か以前から知られていたが、その新たな性質を発見して、それを証明したことから、パスカルの名が付与されている。
一方で、よりシンプルに、パスカルの三角形における数列を左上(または右上)にある列から順にみてみると、以下の通り、これまで紹介してきた図形数等の数列になっている。
単数列 1, 1, 1, 1, 1, 1, 1, 1, 1,…,
自然数の数列 1, 2, 3, 4, 5, 6, 7, 8, 9,…,
三角数の数列 1, 3, 6, 10, 15, 21, 28, 36, 45,…,
三角錐数(正四面体数)の数列 1, 4, 10, 20, 35, 56, 84, 120, 165,…,
因みに、その次の数列 1, 5, 15, 35, 70, 126, 210, 330, 495, …, については、「五胞体数」と呼ばれる数列になっている。「五胞体(ごほうたい)」と呼ばれるのは、4次元単体で、5つの胞で囲まれたものであり、全ての胞が四面体、全ての面が三角形となっているものである。いわば「4次元四面体」に相当し、その意味では「五胞体数」は「4次元正面体数」(「4次元超四面体」とも呼ばれる)に相当するものになっている。同様に、その次の数列 1,6,21,56,126,252,462.792,…, については、「六胞体数」と呼ばれる数列で、「5次元四面体数」(「5次元超々四面体数」)と呼べるものになっている。
なお、パスカルの三角形の横の数列は、当然に2項展開の各項の係数を示しているが、その各行の合計値は2のべき乗(n行目の場合 2n-1)となっている。
1 なお、このような数字の三角形については、パスカルよりも遥か以前から知られていたが、その新たな性質を発見して、それを証明したことから、パスカルの名が付与されている。
(2022年12月28日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年11月06日
世の中は人間よりも生成AIに寛大なのか? -
2025年11月06日
働く人の飲酒量とリスク認識:適正化に気づくのはどのような人か -
2025年11月06日
Meta、ByteDanceのDSA違反の可能性-欧州委員会による暫定的見解 -
2025年11月06日
財政赤字のリスクシナリオ -
2025年11月06日
老後の住宅資産の利活用について考える
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【図形数について(その2)-3次元立体図形に関する図形数、ウェアリングの問題等-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
図形数について(その2)-3次元立体図形に関する図形数、ウェアリングの問題等-のレポート Topへ


















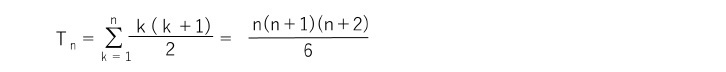
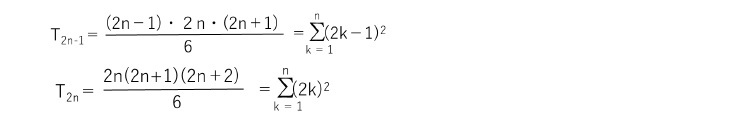
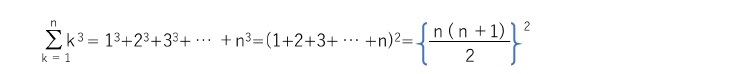
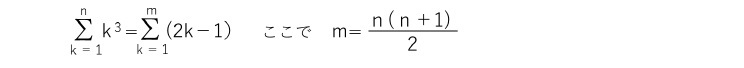

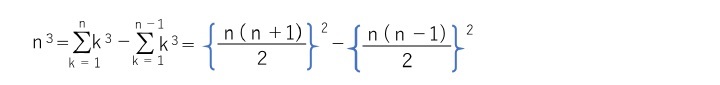


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




