- シンクタンクならニッセイ基礎研究所 >
- 曲線にはどんな種類があって、どう社会に役立っているのか(その5)-サイクロイド(その性質等)-
コラム
2024年05月09日
文字サイズ
- 小
- 中
- 大
はじめに
学生時代に、複雑な算式を図表で表すと、いろんな形の曲線が描かれるのを勉強したと思う。この時には、「へー、そうなんだ」ぐらいの認識でおられた方も多く、むしろ、こうした算式の取扱いに四苦八苦して、結果として得られている曲線が、社会において、あるいは自然界において、どのような形で現れていて、どう役立っているのか、については、あまり説明がなく、殆ど勉強する機会もなかったのではないかと思われる。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。これまでの4回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」、「カテナリー曲線」及び「クロソイド曲線」について報告した。
今回は、「サイクロイド曲線」等について、複数回に分けて報告する。まずは、この研究員の眼では、サイクロイド曲線とはどういうものか、及びその性質等について報告する。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。これまでの4回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」、「カテナリー曲線」及び「クロソイド曲線」について報告した。
今回は、「サイクロイド曲線」等について、複数回に分けて報告する。まずは、この研究員の眼では、サイクロイド曲線とはどういうものか、及びその性質等について報告する。
サイクロイドとは
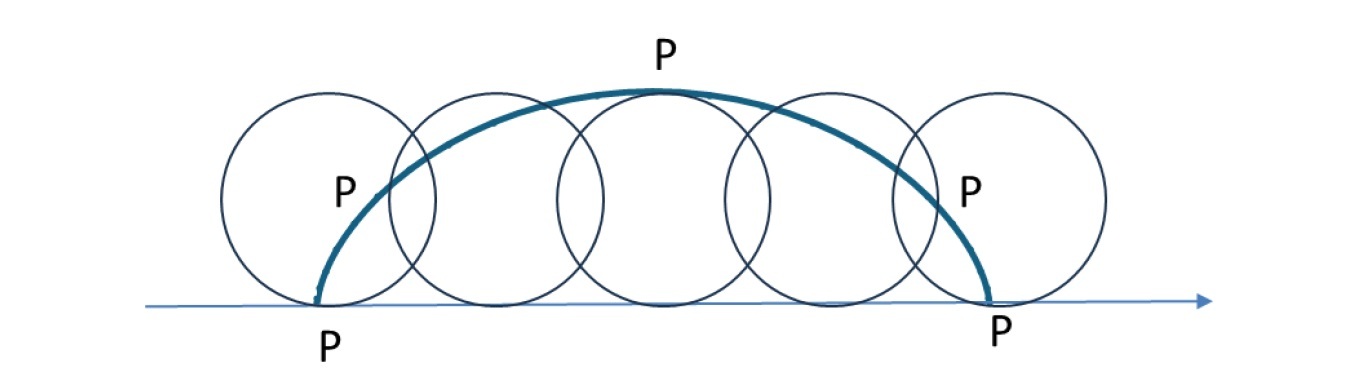
「サイクロイド曲線(cycloid curve)」というのは、一般的には(後掲の図が示しているように)「円が直線上を(滑ることなく)転がるときに、円上のある一点が描く曲線」のことを指している。ただし、より一般的には、「円が他の曲線に沿って転がるときに、円周上の定点が描く軌跡として得られる平面曲線」のことを指している。
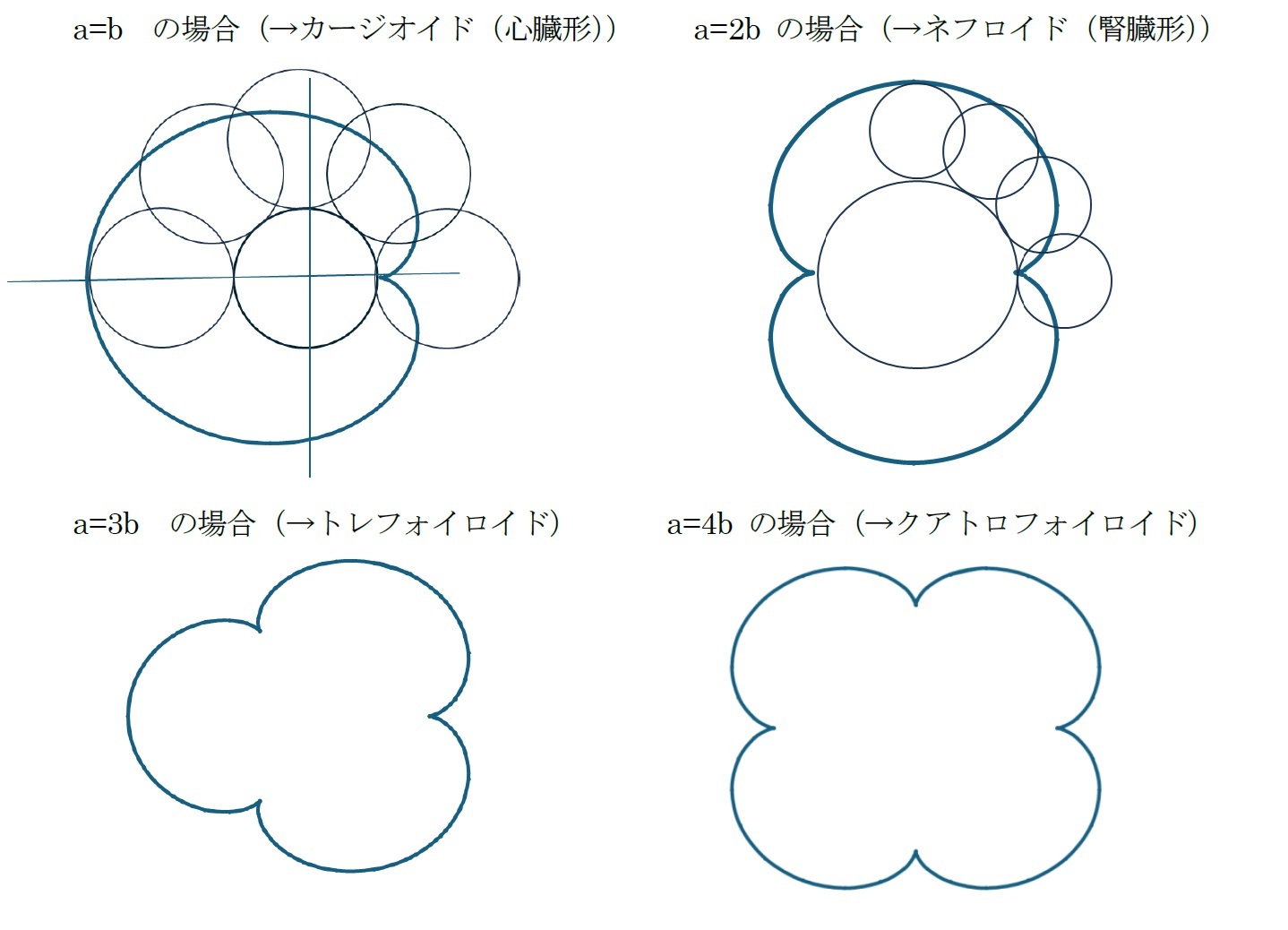
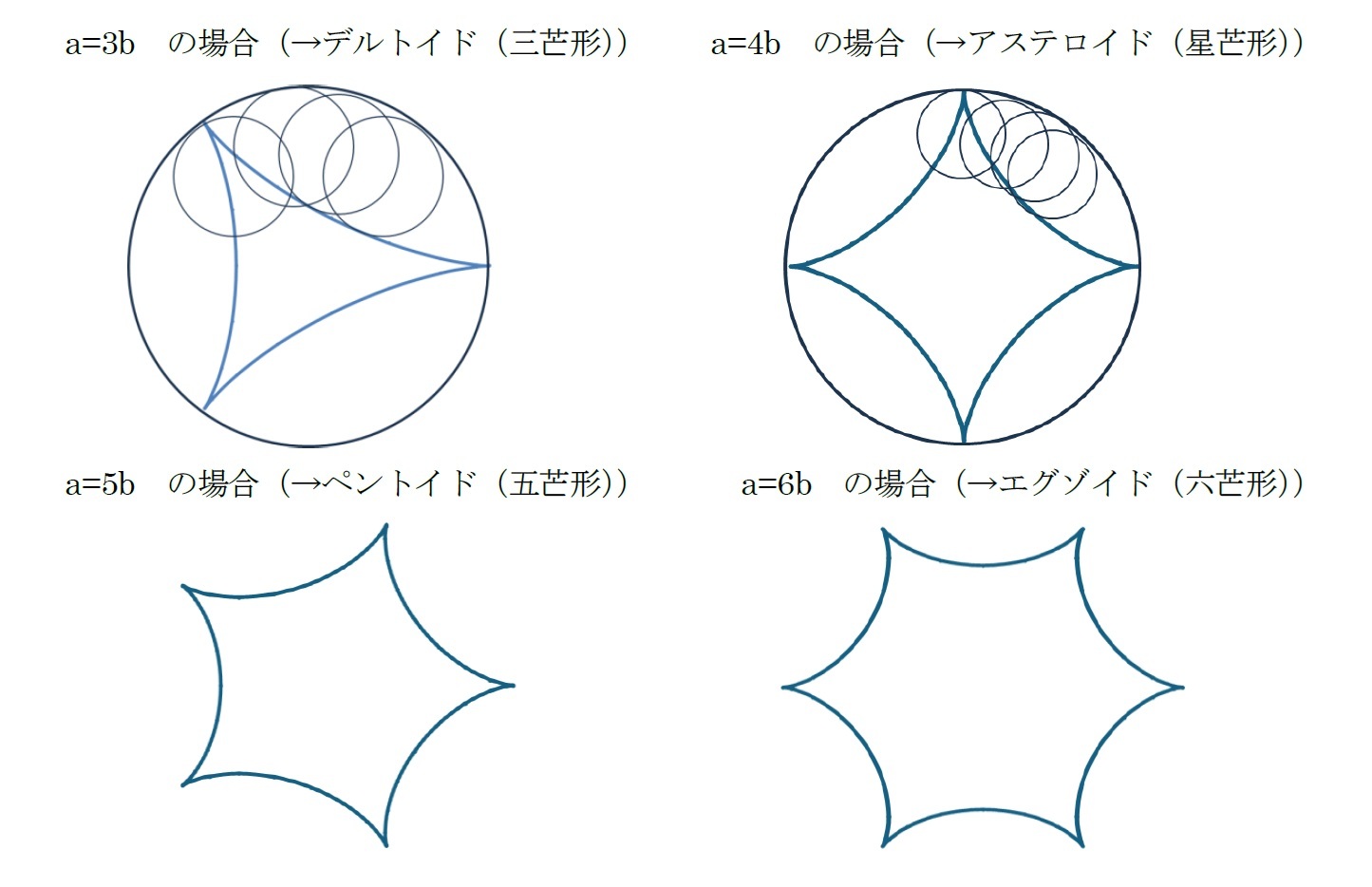
また、円が(直線ではなく)他の円周の外側を転がるときにできる、円周上の1点が描く曲線を「エピサイクロイド(epicycloid)(外サイクロイド)」(又は「ハイパーサイクロイド(hypercycloid)」)、他の円周の内側を転がるときに、円周上の1点が描く曲線を「ハイポサイクロイド(hypocycloid)(内サイクロイド)」と呼んでいる1。
1 なお、日本語では、サイクロイドのことを「擺線(はいせん)」と呼び、エピサイクロイドを「外擺線」、ハイポサイクロイドを「内擺線」、さらには次ページで紹介するトロコイドのことを「余擺線」とも呼んでいる。
また、円が(直線ではなく)他の円周の外側を転がるときにできる、円周上の1点が描く曲線を「エピサイクロイド(epicycloid)(外サイクロイド)」(又は「ハイパーサイクロイド(hypercycloid)」)、他の円周の内側を転がるときに、円周上の1点が描く曲線を「ハイポサイクロイド(hypocycloid)(内サイクロイド)」と呼んでいる1。
1 なお、日本語では、サイクロイドのことを「擺線(はいせん)」と呼び、エピサイクロイドを「外擺線」、ハイポサイクロイドを「内擺線」、さらには次ページで紹介するトロコイドのことを「余擺線」とも呼んでいる。
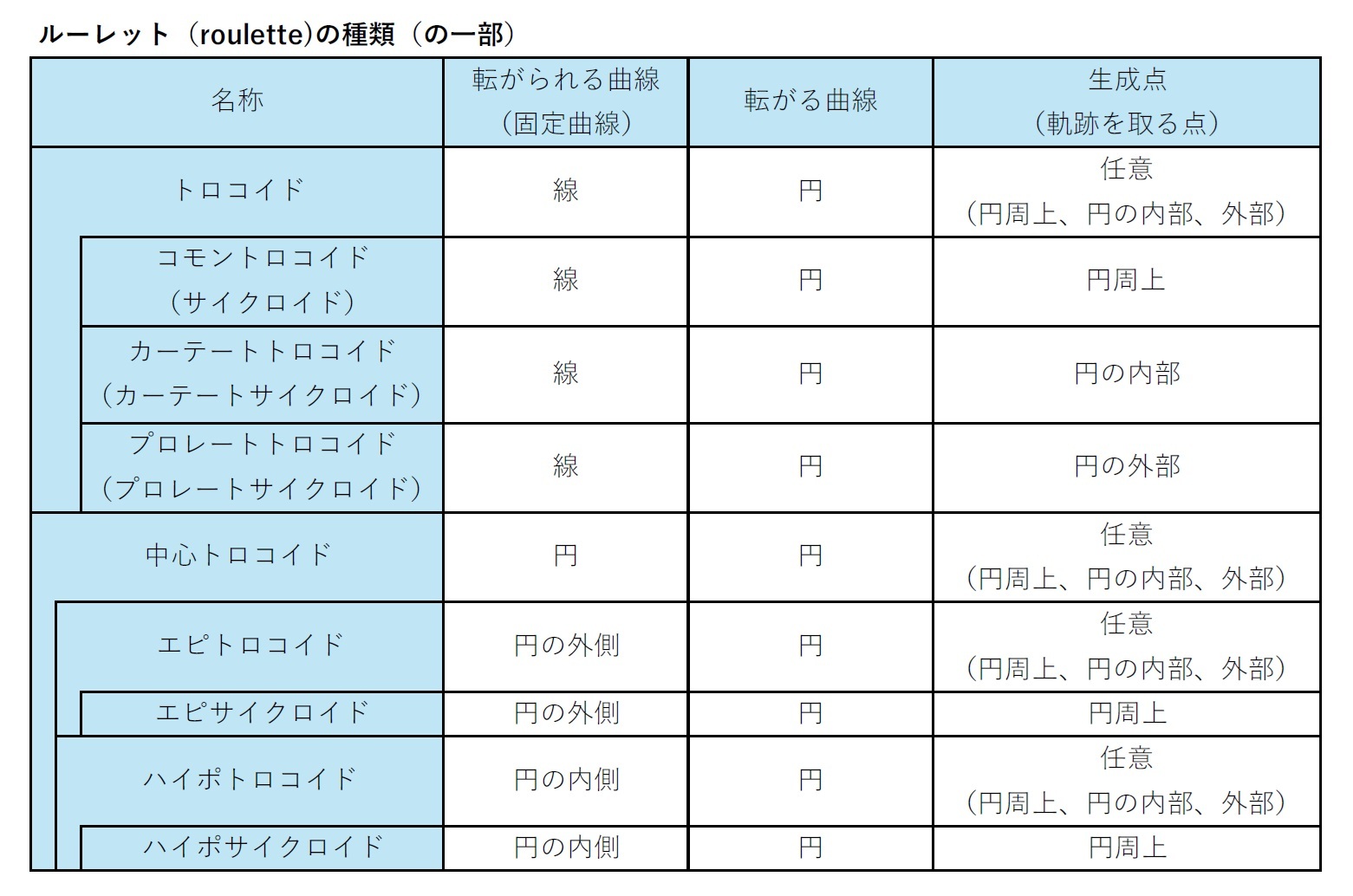
(参考)トロコイド曲線
なお、「サイクロイド」を含む、より一般的な概念があり、これについての用語の使用は必ずしも統一されていない場合もあるようだが、例えば以下のような名称での分類がなされている。
「トロコイド(trochoid)」は、幅広い意味では「円がある曲線(直線や円を含む)に沿って転がるときに、その円周上、円の内部又は外部にある定点が描く曲線」のことを指している2。ただし、通常は狭義の意味で「円が直線に沿って転がるときに、その円周上、円の内部又は外部にある定点が描く曲線」のことを指している(以下の図表を含めて、今回のレポートではこの定義に基づいて説明している)。
このとき、定点が、円周上にある場合「コモン(common)」(又は「サイクロイド」)、円の内部にある場合「カーテート(curtate)(収縮)」、円の外部にある場合「プロレート(prolate)(拡張)」と呼ばれる。例えば、自転車で直線上を走行するときに、ペダルの描く軌道が「カーテートトロコイド(又はカーテートサイクロイドとも呼ばれる)」となる。
また、他の円に沿って転がるときで、その円周上、円の内部又は外部にある定点が描く曲線で、円の円周の外側を転がる場合「エピトロコイド(epitrochoid)(外トロコイド)」、円周の内側を転がる場合「ハイポトロコイド(hypotrochoid)(内トロコイド)」、これらを合わせて、「中心トロコイド(centered trochoid)」と呼ばれる。
以上をまとめると、概ね以下の図表のようになる。
「トロコイド(trochoid)」は、幅広い意味では「円がある曲線(直線や円を含む)に沿って転がるときに、その円周上、円の内部又は外部にある定点が描く曲線」のことを指している2。ただし、通常は狭義の意味で「円が直線に沿って転がるときに、その円周上、円の内部又は外部にある定点が描く曲線」のことを指している(以下の図表を含めて、今回のレポートではこの定義に基づいて説明している)。
このとき、定点が、円周上にある場合「コモン(common)」(又は「サイクロイド」)、円の内部にある場合「カーテート(curtate)(収縮)」、円の外部にある場合「プロレート(prolate)(拡張)」と呼ばれる。例えば、自転車で直線上を走行するときに、ペダルの描く軌道が「カーテートトロコイド(又はカーテートサイクロイドとも呼ばれる)」となる。
また、他の円に沿って転がるときで、その円周上、円の内部又は外部にある定点が描く曲線で、円の円周の外側を転がる場合「エピトロコイド(epitrochoid)(外トロコイド)」、円周の内側を転がる場合「ハイポトロコイド(hypotrochoid)(内トロコイド)」、これらを合わせて、「中心トロコイド(centered trochoid)」と呼ばれる。
以上をまとめると、概ね以下の図表のようになる。
2 トロコイド自体も、「ルーレット(roulette)」(日本語では「輪転曲線」とも呼ばれる)と呼ばれる、より一般的な曲線の一種となっている。則ち、ルーレット>トロコイド>サイクロイド という関係になっている。ルーレットは、「ある曲線を他の曲線に沿って転がしたときに、回転する曲線に取り付けられた定点によって生成される曲線」となる。回転する曲線が円の場合(狭義の意味では、直線上を転がる場合)がトロコイドで、さらに定点が円周上にある場合がサイクロイドになる。
今回のレポートでは、このうちのサイクロイド、エピサイクロイド、ハイポサイクロイドに焦点を当てて説明する。
各種の具体的なサイクロイドの図形は、以下の通りとなっている。
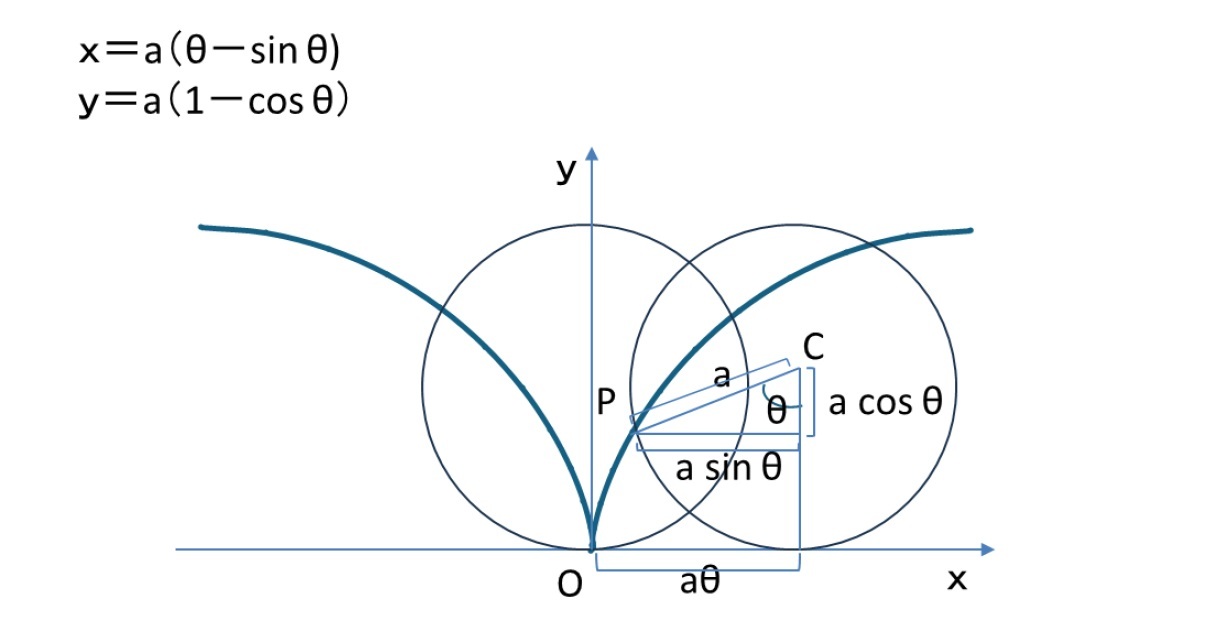
サイクロイドについて
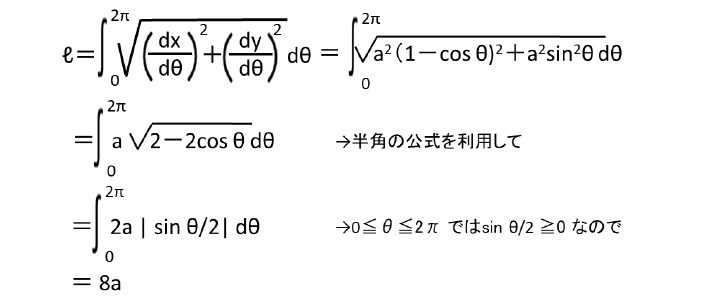
この「サイクロイド」の弧長(円が1回転した時の定点の軌跡の長さ)ℓと面積(直線と弧の間に囲まれた部分)Sについては、以下の通りとなっている4。
3 関数を、媒介変数(パラメータ:parameter)を用いて表現したもの。「パラメータ表示」とも言われる。
4 これらの事実については、ガリレオ・ガリレイが発見したとされるが、彼は証明を与えなかったようだ。孤の長さについては、英国の建築家・天文学者であるクリストファー・レンが1658年に証明している。
(2024年05月09日「研究員の眼」)
このレポートの関連カテゴリ
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月30日
潜在成長率は変えられる-日本経済の本当の可能性 -
2025年10月30日
米FOMC(25年10月)-市場予想通り、政策金利を▲0.25%引き下げ。バランスシート縮小を12月1日で終了することも決定 -
2025年10月30日
試練の5年に踏み出す中国(後編)-「第15次五カ年計画」建議にみる、中国のこれからの針路 -
2025年10月30日
米国で進む中間期の選挙区割り変更-26年の中間選挙を見据え、与野党の攻防が激化 -
2025年10月29日
生活習慣病リスクを高める飲酒の現状と改善に向けた対策~男女の飲酒習慣の違いに着目して
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【曲線にはどんな種類があって、どう社会に役立っているのか(その5)-サイクロイド(その性質等)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
曲線にはどんな種類があって、どう社会に役立っているのか(その5)-サイクロイド(その性質等)-のレポート Topへ


















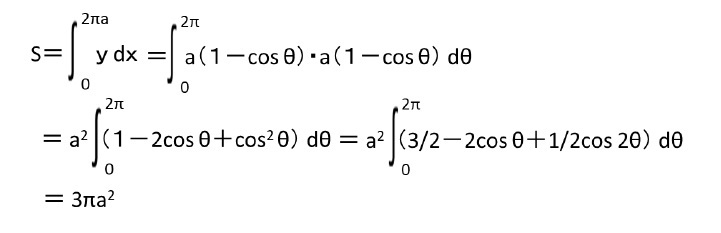

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




