- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 曲線にはどんな種類があって、どう社会に役立っているのか(その3)-カテナリー曲線-
コラム
2024年01月16日
文字サイズ
- 小
- 中
- 大
はじめに
学生時代に、複雑な算式を図表で表すと、いろんな形の曲線が描かれるのを勉強したと思う。この時には、「へー、そうなんだ」ぐらいの認識でおられた方も多く、むしろ、こうした算式の取扱いに四苦八苦して、結果として得られている曲線が、社会において、あるいは自然界において、どのような形で現れていて、どう役立っているのか、については、あまり説明がなく、殆ど勉強する機会もなかったのではないかと思われる。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。これまでの2回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」について報告した。
今回は、「カテナリー曲線」について報告する。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。これまでの2回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」について報告した。
今回は、「カテナリー曲線」について報告する。
カテナリー曲線とは
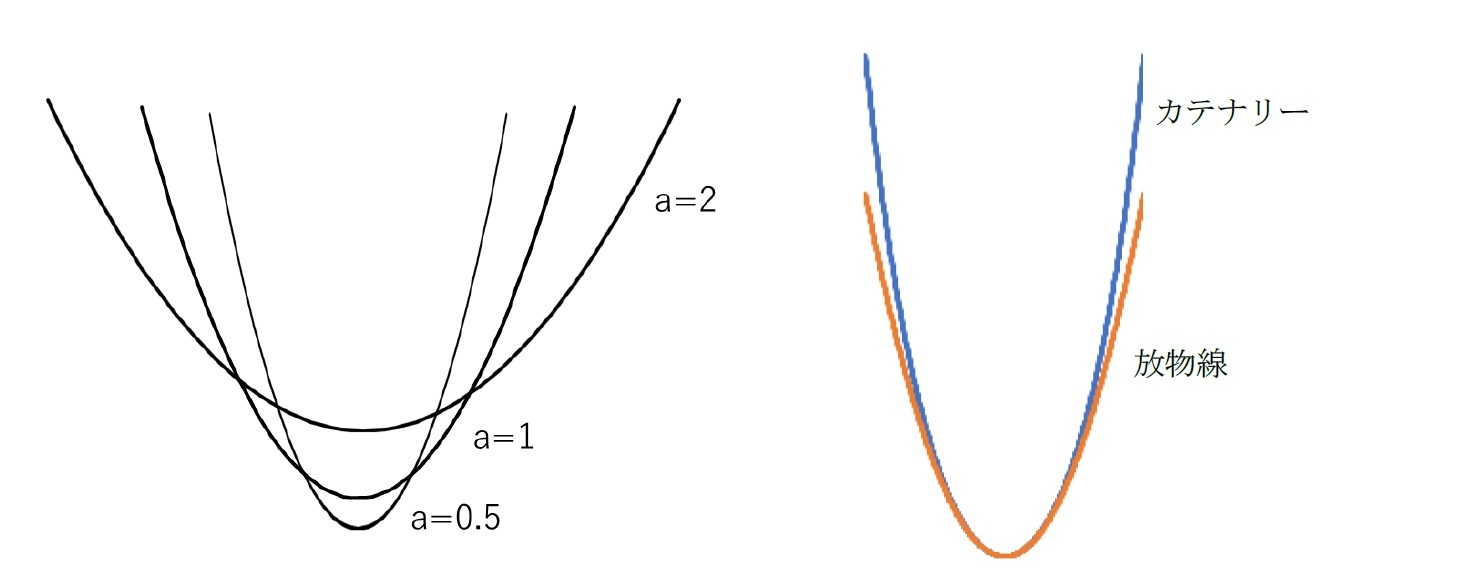
放物線との違いは
で近似されることになり、これはy軸で対称な放物線となる。
カテナリー曲線の性質
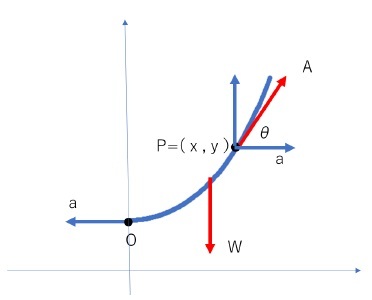
カテナリー曲線の形状は、まさに線状の物体に加わる重力とそれぞれの部分に加わる両サイドからの張力のバランスの中で形成されている。この関係を算式で表すことにより、微分方程式を作成し、その微分方程式を解くことで、カテナリー曲線の上記の算式が得られることになる。
具体的には、以下の通りである。
具体的には、以下の通りである。
A cosθ =a
となる。一方で、垂直方向の釣り合いから、弧OPの重量をWとすると
A sinθ=W
ここで、弧OPの単位長さ当たりの重さをkとすると、曲線の長さを算出する式を用いて、以下の通りに表される。
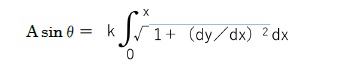
これらの2式からAを消去すると
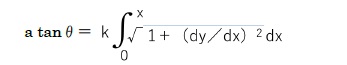
よって、
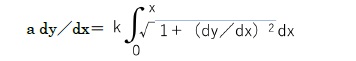
この微分方程式を、初期条件y(0)=0、dy/dx(0)=0 の下で解くことで、
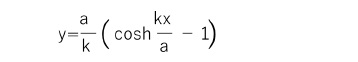
となる。
となる。一方で、垂直方向の釣り合いから、弧OPの重量をWとすると
A sinθ=W
ここで、弧OPの単位長さ当たりの重さをkとすると、曲線の長さを算出する式を用いて、以下の通りに表される。
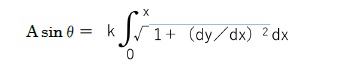
これらの2式からAを消去すると
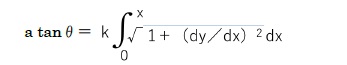
よって、
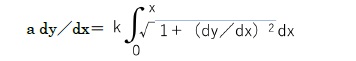
この微分方程式を、初期条件y(0)=0、dy/dx(0)=0 の下で解くことで、
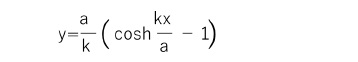
となる。
カテナリー曲線が観察される例
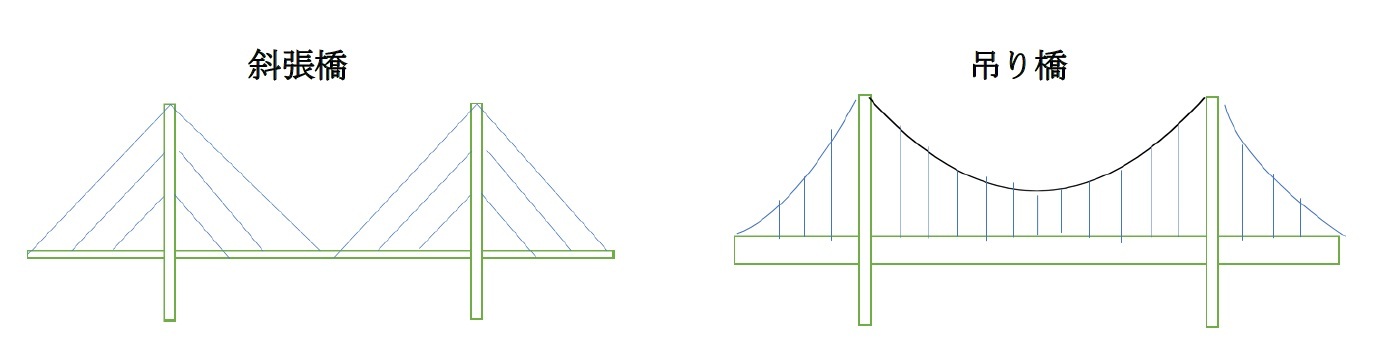
(参考)吊り橋
これに対して、一般的な吊り橋の形状については、カテナリー曲線になる場合と放物線に近い形状となる場合がある(なお、斜張橋が塔と橋桁をケーブルで直結しているのに対して、吊り橋は塔の間にまず渡したメインケーブルがあり、そこから垂らしたハンガーロープで橋桁を吊っている)。
太くて重いケーブルに軽い橋桁が支えられているような場合で、橋全体を1本の鎖のように考えることができる場合、カテナリー曲線になる。一方で、車が通るような吊り橋で、ケーブルに比べて格段に重量の大きな水平の橋桁を持つ場合、ケーブルは放物線(に近い形)を描くことになる。
これについては、先のカテナリー曲線の算式において、垂直方向の釣り合いが、点Pにおける張力と、弧OPの重量ではなく、弧OPの下にある床の重量とでバランスされる形になることから、
A sinθ=弧OPの下にある床の重量
弧OPの下にある床の単位長さ当たりの重量をkとすると、上記右辺はkxと表されることから、
a tanθ=kx
よって、
a dy/dx=kx
初期条件y(0)=0の下で解くと、
y=(k/2a)x2
となり、これはy軸で対称な放物線となる。
太くて重いケーブルに軽い橋桁が支えられているような場合で、橋全体を1本の鎖のように考えることができる場合、カテナリー曲線になる。一方で、車が通るような吊り橋で、ケーブルに比べて格段に重量の大きな水平の橋桁を持つ場合、ケーブルは放物線(に近い形)を描くことになる。
これについては、先のカテナリー曲線の算式において、垂直方向の釣り合いが、点Pにおける張力と、弧OPの重量ではなく、弧OPの下にある床の重量とでバランスされる形になることから、
A sinθ=弧OPの下にある床の重量
弧OPの下にある床の単位長さ当たりの重量をkとすると、上記右辺はkxと表されることから、
a tanθ=kx
よって、
a dy/dx=kx
初期条件y(0)=0の下で解くと、
y=(k/2a)x2
となり、これはy軸で対称な放物線となる。
有名なサンフランシスコの「ゴールデンゲートブリッジ」の殆どのケーブルは放物線を描いているようだ。
なお、ケーブル等の重量が無視できない場合の吊り橋のケーブルは、より複雑な形状となる。
なお、ケーブル等の重量が無視できない場合の吊り橋のケーブルは、より複雑な形状となる。
(2024年01月16日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月17日
「SDGs疲れ」のその先へ-2015年9月国連採択から10年、2030年に向け問われる「実装力」 -
2025年10月16日
EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- -
2025年10月16日
再び不安定化し始めた米中摩擦-経緯の振り返りと今後想定されるシナリオ -
2025年10月15日
インド消費者物価(25年10月)~9月のCPI上昇率は1.5%に低下、8年ぶりの低水準に -
2025年10月15日
「生活の質」と住宅価格の関係~教育サービス・治安・医療サービスが新築マンション価格に及ぼす影響~
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【曲線にはどんな種類があって、どう社会に役立っているのか(その3)-カテナリー曲線-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
曲線にはどんな種類があって、どう社会に役立っているのか(その3)-カテナリー曲線-のレポート Topへ


















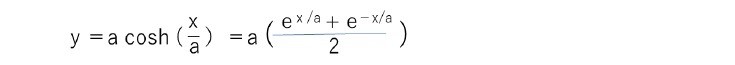





 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




