- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 曲線にはどんな種類があって、どう社会に役立っているのか(その12)-螺旋と渦巻の応用-
コラム
2025年08月20日
文字サイズ
- 小
- 中
- 大
はじめに
学生時代に、複雑な算式を図表で表すと、いろんな形の曲線が描かれるのを勉強したと思う。この時には、「へー、そうなんだ」ぐらいの認識でおられた方も多く、むしろ、こうした算式の取扱いに四苦八苦して、結果として得られている曲線が、社会において、あるいは自然界において、どのような形で現れていて、どう役立っているのか、については、あまり説明がなく、殆ど勉強する機会もなかったのではないかと思われる。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。前々回までの9回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」、「カテナリー曲線」、「クロソイド曲線」、「サイクロイド曲線・トロコイド曲線」、「リサージュ曲線」及び「バラ曲線」、「カッシーニの卵形線」、「レムニスケート」、「デカルトの正葉線」について報告した。
前々回から、各種の「螺旋(らせん)」や「渦巻」について、3回に分けて報告している。前々回は、各種の「螺旋」や「渦巻」の主要な種類について、その数式での表現と特性等について、簡単に紹介した。前回は、日常生活の中で見ることができる「螺旋」や「渦巻」について紹介した。
今回は、これらの「螺旋」や「渦巻」が社会の中でどのように役立っているのかについて、前回紹介した内容と一部重複する部分も含めて、いくつか紹介する。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。前々回までの9回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」、「カテナリー曲線」、「クロソイド曲線」、「サイクロイド曲線・トロコイド曲線」、「リサージュ曲線」及び「バラ曲線」、「カッシーニの卵形線」、「レムニスケート」、「デカルトの正葉線」について報告した。
前々回から、各種の「螺旋(らせん)」や「渦巻」について、3回に分けて報告している。前々回は、各種の「螺旋」や「渦巻」の主要な種類について、その数式での表現と特性等について、簡単に紹介した。前回は、日常生活の中で見ることができる「螺旋」や「渦巻」について紹介した。
今回は、これらの「螺旋」や「渦巻」が社会の中でどのように役立っているのかについて、前回紹介した内容と一部重複する部分も含めて、いくつか紹介する。
螺旋や渦巻の応用
前回の研究員の眼で紹介したように、螺旋や渦巻は幅広くいろいろな場面で観測される。これはまさに自然現象の中で、これらが「自然に」現われてくる現象であることによる。即ち、一般の人々にとっても、螺旋や渦巻は、ある意味で慣れ親しんだ図形であり、その躍動感があり、一種力強さを感じさせる要素から、時には恐怖等のネガティブな印象を受けることもあるかもしれないが、一方である種の生命力を感じさせる要素もあって、ポジティブな印象を与えることも多いものと思われる。同じことの繰り返しでありながら、決して同じ位置に戻ることなく、無限に発散あるいはある1点に収束していく様子は、何となく畏怖の感覚と共に心地よさを感じさせるものともなっている。
従って、こうした自然な現象を模したものが、古代文明の時代から、人工的にも各種の場面で利用され現れてきているというのも極めて納得感のあることだといえるのではないだろうか。
その結果として、螺旋や渦巻は、数学や物理や化学や生物といった自然科学の研究分野においてのみならず、各種の工学が関連する技術的・実用的な分野や経済学等の社会科学の研究分野、さらには音楽や美術等の芸術分野等において、幅広く使用されてきている。加えて、螺旋は無限や輪廻等を象徴するものとして、各種の宗教における観念等においても引用されてきている。我々の日常生活においても、螺旋やスパイラルといった用語が、直線的でない、段階的な発展や深化を表現するため等に使用されているのをよく見かけるのではないだろうか。
その意味で、螺旋や渦巻は人間と極めて関係の深い曲線だといえるだろう。
従って、こうした自然な現象を模したものが、古代文明の時代から、人工的にも各種の場面で利用され現れてきているというのも極めて納得感のあることだといえるのではないだろうか。
その結果として、螺旋や渦巻は、数学や物理や化学や生物といった自然科学の研究分野においてのみならず、各種の工学が関連する技術的・実用的な分野や経済学等の社会科学の研究分野、さらには音楽や美術等の芸術分野等において、幅広く使用されてきている。加えて、螺旋は無限や輪廻等を象徴するものとして、各種の宗教における観念等においても引用されてきている。我々の日常生活においても、螺旋やスパイラルといった用語が、直線的でない、段階的な発展や深化を表現するため等に使用されているのをよく見かけるのではないだろうか。
その意味で、螺旋や渦巻は人間と極めて関係の深い曲線だといえるだろう。
アルキメデスの螺旋の応用
アルキメデスの螺旋の数学における利用として、「円積問題」(英語では「squaring the circle(円の正方形化)」)と「角の三等分問題」がある。これらの問題については、以前の研究員の眼「ギリシアの3大作図問題-数学を通じて、ギリシアという国の歴史的位置付けの重みを再認識してみませんか-」(2017.6.19)等で紹介した。これらは、「コンパスと定規を使用して、限られた数の手順のみを使用して」、「与えられた円の面積を持つ正方形を作成」したり、「任意の角を三等分」したりする問題である。これらが不可能であることは、前者は1882年にドイツ人数学者カール・フェルディナント・フォン・リンデマン(Carl Louis Ferdinand von Lindemann)によって解決され、後者は1837年にフランス人数学者ピエール・ローラン・ヴァンツェル(Pierre Laurent Wantzel)によって解決された。
一方で、補助的な道具を使用したり、コンパスと定規を使った無限の操作を可能にしたり、あるいは特定の非ユークリッド幾何学1で操作を実行したりすることで、これらは可能になる。その1つの方法として、アルキメデスの螺旋2を利用するものがある。
一方で、補助的な道具を使用したり、コンパスと定規を使った無限の操作を可能にしたり、あるいは特定の非ユークリッド幾何学1で操作を実行したりすることで、これらは可能になる。その1つの方法として、アルキメデスの螺旋2を利用するものがある。
 具体的には、例えば「角の三等分」については、以下の通りである。
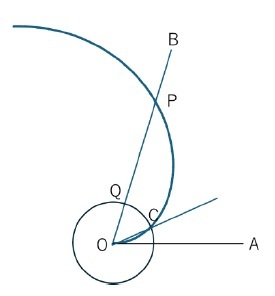
具体的には、例えば「角の三等分」については、以下の通りである。角AOBを三等分することを考える。
(1) アルキメデスの螺旋と線分OBの交点をPとする。
(2) 線分OPを三等分する点をQ(即ち、OQはOPの3分の1)とする。
(3) 中心O、半径OQの円を描く。
(4) 中心Oの円と螺旋が交差する点をCとする。
(5) 角AOCは角AOBの3分の1となる。
(これは、アルキメデスの螺旋が極方程式r=aθで表されることから明らかである)
アルキメデスの螺旋は、現実の世界においても幅広く利用されている。
前回の研究員の眼で、レコードやCD、蚊取り線香等での例について紹介したが、さらに例えば以下のような応用がされている。
時計の「バランススプリング(ひげぜんまい)」は、機械式時計のテンプ(調速樹)に取り付けられたバネで、時計が動いているときに、ひげぜんまいによってテンプが共振周波数で振動し、時計の歯車の回転速度、つまり針の動きの速度が制御される。調整レバーが取り付けられていることが多く、これを使用してバネの自由長を変更し、時計の速度を調整できる。このひげぜんまいのコイルはアルキメデスの螺旋となっている。
「螺旋アンテナ」は、らせん状の形状をした無線周波数アンテナの一種で、広範囲の周波数で操作できる。周波数に依存しない対数螺旋アンテナもあるが、アルキメデスの螺旋アンテナが最も一般的である。螺旋アンテナは、巻き線によって小型化され、非常に小さな構造になっている。
空気や冷媒を圧縮する装置である「スクロールコンプレッサー(スクロールポンプ、スクロール真空ポンプとも呼ばれる)」は、2つの交互に配置されたスクロールを使用して、液体や気体などの流体を汲み上げ、圧縮・加圧する。この羽根の形状がアルキメデスの螺旋やインボリュートやハイブリッド曲線になっている。多くの場合、スクロールの1つは固定され、もう1つは回転せずに偏心して軌道を描き、スクロール間の流体ポケットを捕捉して、汲み上げ、圧縮・加圧する。
「スパイラルプラッター(spiral plater)」は、液体サンプルをスパイラルパターンでペトリ皿に分注するために使用される機器で、サンプル中の微生物の数を決定し、細菌濃度を定量化する等の目的で、食品、牛乳、乳製品、化粧品の微生物学的試験に広く使用されているが、ここでもアルキメデスの螺旋が使用されている。
また、神経疾患の診断において、患者にアルキメデスの螺旋を描くように頼む(曲線をなぞり、震えでどれだけずれるかを調べる)ことで、振戦(震え)を定量化することに役立っている。
1 ユークリッド幾何学の平行線公準(1つの直線が2つの直線に交わってできる同じ側の内角の和が2直角より小さいならば、この2つの直線を(限りなく)延長すると、2直角より小さい角のある側において交わる)が成り立たないとして成立する幾何学の総称
2 アルキメデスは、その論文「螺旋について」において、アルキメデスの螺旋を用いて、円を正方形にし、角を三等分する方法を示している。
放物螺旋の応用
「集光型太陽光発電(CSP、集光型太陽熱発電とも呼ばれる)」システムは、鏡やレンズを使用して広い面積の太陽光を受信機に集中させることで太陽光発電を行うもので、集中した光が熱(太陽熱エネルギー)に変換されると電気が生成され、発電機に接続された熱機関(通常は蒸気タービン)を駆動するか、熱化学反応に電力を供給する。放物螺旋は、この集光型太陽光発電所のミラーの効率的なレイアウトとなっている。
また、サイクロトロンの設計において、サイクロトロン内の粒子が辿る軌道は、放物螺旋で近似されている。
さらに、植物の成長において、例えば植物の茎がどのように成長して葉を最適な位置に配置するかを説明するのに放物螺旋が役立っている。
また、サイクロトロンの設計において、サイクロトロン内の粒子が辿る軌道は、放物螺旋で近似されている。
さらに、植物の成長において、例えば植物の茎がどのように成長して葉を最適な位置に配置するかを説明するのに放物螺旋が役立っている。
双曲螺旋の応用
双曲螺旋の応用としては、前々回の研究員の眼で紹介した例が挙げられる。
陸上競技の200mと400mレースのスタートマークは、双曲螺旋に沿ってずらされた位置に配置される。これにより、同心円状のレーンに制限されたランナー全員が、フィニッシュラインまで同じ長さの経路を持つことが保証される。一方で、走者がスタート後に内側のレーンに移動する長距離レースでは、代わりに別の螺旋(円のインボリュート)が使用される。
さらに、双曲螺旋は、一部の螺旋銀河の形状をモデル化するために使用される。また、建築ではコリント式の柱の渦巻きのデザインに使用され、さらに螺旋階段やその他の螺旋構造の軸の上向きの透視図となっている。
陸上競技の200mと400mレースのスタートマークは、双曲螺旋に沿ってずらされた位置に配置される。これにより、同心円状のレーンに制限されたランナー全員が、フィニッシュラインまで同じ長さの経路を持つことが保証される。一方で、走者がスタート後に内側のレーンに移動する長距離レースでは、代わりに別の螺旋(円のインボリュート)が使用される。
さらに、双曲螺旋は、一部の螺旋銀河の形状をモデル化するために使用される。また、建築ではコリント式の柱の渦巻きのデザインに使用され、さらに螺旋階段やその他の螺旋構造の軸の上向きの透視図となっている。
(2025年08月20日「研究員の眼」)
関連レポート
- ギリシアの3大作図問題-数学を通じて、ギリシアという国の歴史的位置付けの重みを再認識してみませんか-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その11)-螺旋と渦巻の実例-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その10)-螺旋と渦巻の種類-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その9)-カッシーニの卵形線・レムニスケート等-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その8)-リサージュ曲線・バラ曲線-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その7)-サイクロイド・トロコイド(その応用)-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その6)-トロコイド・リマソン・カージオイド等-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その5)-サイクロイド(その性質等)-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その4)-クロソイド曲線-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その3)-カテナリー曲線-
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/13 | 数字の「27」に関わる各種の話題-27は3の3乗だが- | 中村 亮一 | 研究員の眼 |
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月20日
持続可能なESGを求めて-目標と手段とを取り違えないこと -
2025年11月20日
「ラブブ」とは何だったのか-SNS発の流行から考える“リキッド消費” -
2025年11月19日
1ドル155円を突破、ぶり返す円安の行方~マーケット・カルテ12月号 -
2025年11月19日
年金額改定の本来の意義は実質的な価値の維持-年金額改定の意義と2026年度以降の見通し(1) -
2025年11月19日
日本プロ野球の監督とMLBのマネージャー~訳語が仕事を変えたかもしれない~
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【曲線にはどんな種類があって、どう社会に役立っているのか(その12)-螺旋と渦巻の応用-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
曲線にはどんな種類があって、どう社会に役立っているのか(その12)-螺旋と渦巻の応用-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




