- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 曲線にはどんな種類があって、どう社会に役立っているのか(その9)-カッシーニの卵形線・レムニスケート等-
コラム
2024年11月06日
文字サイズ
- 小
- 中
- 大
はじめに
学生時代に、複雑な算式を図表で表すと、いろんな形の曲線が描かれるのを勉強したと思う。この時には、「へー、そうなんだ」ぐらいの認識でおられた方も多く、むしろ、こうした算式の取扱いに四苦八苦して、結果として得られている曲線が、社会において、あるいは自然界において、どのような形で現れていて、どう役立っているのか、については、あまり説明がなく、殆ど勉強する機会もなかったのではないかと思われる。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。これまでの8回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」、「カテナリー曲線」、「クロソイド曲線」、「サイクロイド曲線・トロコイド曲線」、「リサージュ曲線」及び「バラ曲線」について報告した。
今回は、「カッシーニの卵形線(らんけいせん)」、「レムニスケート」、「デカルトの正葉線」と呼ばれるものについて、報告する。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。これまでの8回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」、「カテナリー曲線」、「クロソイド曲線」、「サイクロイド曲線・トロコイド曲線」、「リサージュ曲線」及び「バラ曲線」について報告した。
今回は、「カッシーニの卵形線(らんけいせん)」、「レムニスケート」、「デカルトの正葉線」と呼ばれるものについて、報告する。
カッシーニの卵形線とは
「カッシーニの卵形線(Cassinian oval)」1というのは、以下の直交座標の方程式で表される四次曲線である。
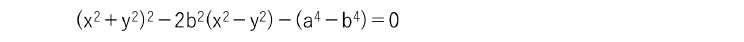
これは、「2つの定点(-b,0)、(b,0)に対して、動点P(x,y)を考えた場合、2つの定点からPへのそれぞれ距離の積がa2であるような点Pの軌跡」2となる(2つの定点は「焦点」と呼ばれる)。
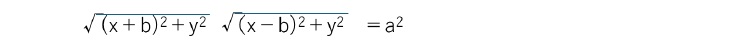
この式の両辺を二乗して変形することで、先の四次方程式が得られる。なお、先の四次方程式に x=r cosθ、y=r sinθ を代入することにより、r2に関する二次方程式が得られるので、これを解いて、以下の極座標の方程式が得られる。
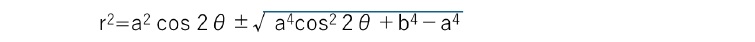
カッシーニの卵形線(Cassinian oval)という名称は、17世紀後半にこの形状を研究したイタリア出身のフランスの天文学者ジョヴァンニ・ドメニコ・カッシーニ(Giovanni Domenico Cassini)3に因んでいる。カッシーニは、別の天体の周りを周回する惑星は、これらの卵形線の1つに沿って移動し、その周りを周回される天体は卵形線の1つの焦点にある、と信じていた4。
カッシーニの卵形線は、x軸とy軸に対して対称な図形で、aとbの大小関係によって、以下の通りとなる。
・a<b の時、2つのループに分かれ、
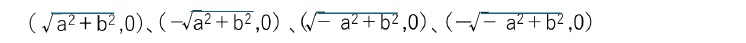
の4点でx軸と交わる。
・a=b の時、「レムニスケート(lemniscate)」と呼ばれる図形になり、

の3点でx軸と交わる。
・a>b の時、1つのループとなり、

の2点でx軸と交わる。
さらに、このケースにおいて、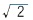 ・b >a>bの時、ループは凹型(凹みを有する)となり、a≧
・b >a>bの時、ループは凹型(凹みを有する)となり、a≧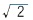 ・bの時、凸型(凹みを有さない)となる。
・bの時、凸型(凹みを有さない)となる。
具体的には、以下のような図形となっている。
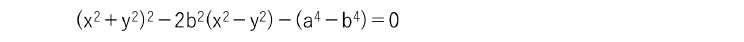
これは、「2つの定点(-b,0)、(b,0)に対して、動点P(x,y)を考えた場合、2つの定点からPへのそれぞれ距離の積がa2であるような点Pの軌跡」2となる(2つの定点は「焦点」と呼ばれる)。
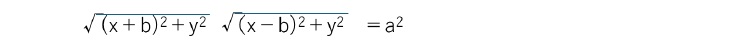
この式の両辺を二乗して変形することで、先の四次方程式が得られる。なお、先の四次方程式に x=r cosθ、y=r sinθ を代入することにより、r2に関する二次方程式が得られるので、これを解いて、以下の極座標の方程式が得られる。
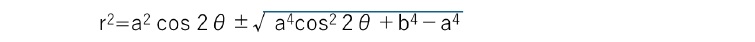
カッシーニの卵形線(Cassinian oval)という名称は、17世紀後半にこの形状を研究したイタリア出身のフランスの天文学者ジョヴァンニ・ドメニコ・カッシーニ(Giovanni Domenico Cassini)3に因んでいる。カッシーニは、別の天体の周りを周回する惑星は、これらの卵形線の1つに沿って移動し、その周りを周回される天体は卵形線の1つの焦点にある、と信じていた4。
カッシーニの卵形線は、x軸とy軸に対して対称な図形で、aとbの大小関係によって、以下の通りとなる。
・a<b の時、2つのループに分かれ、
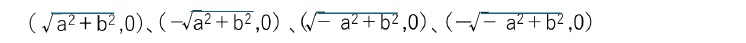
の4点でx軸と交わる。
・a=b の時、「レムニスケート(lemniscate)」と呼ばれる図形になり、

の3点でx軸と交わる。
・a>b の時、1つのループとなり、

の2点でx軸と交わる。
さらに、このケースにおいて、
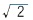 ・b >a>bの時、ループは凹型(凹みを有する)となり、a≧
・b >a>bの時、ループは凹型(凹みを有する)となり、a≧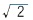 ・bの時、凸型(凹みを有さない)となる。
・bの時、凸型(凹みを有さない)となる。具体的には、以下のような図形となっている。
1 「oval」は、幾何学で卵形や長円形、楕円や楕円に似た曲線であり、この言葉は、卵を意味するラテン語のovumに由来している。
2 2つの定点からの距離の和、差、積、商が一定である点の軌跡は、以下の通りとなっている((1)、(2)及び(4)については、研究員の眼「曲線にはどんな種類があって、どう社会に役立っているのか(その1)-円錐曲線(楕円、放物線、双曲線)とは-」(2023.10.16)で紹介、説明している)。
(1)和が一定→楕円、(2)差が一定→双曲線、(3)積が一定→カッシーニの卵形線、(4)商(比)が一定→アポロ二ウスの円
3 土星の4つの衛星を発見し、1675年には土星の環に隙間(カッシーニの間隙)があることを発見する等、惑星観測で多くの功績がある。NASA(アメリカ航空宇宙局)とESA(ヨーロッパ宇宙機関)が1997年に共同で開発して打ち上げた土星探査機は彼の息子のジョバンニ・カッシーニに因んで「カッシーニ」と名付けられており、月にあるクレーターは、彼とジョバンニに因んで「カッシーニ」と名付けられている。
4 ケプラーの第1法則(楕円軌道の法則)により、太陽系の惑星は太陽を焦点の1つとする楕円軌道を描いている。
5 円周を回転して得られる回転面
レムニスケートとは
「レムニスケート(lemniscate)」というのは、以下の極座標の方程式で表される曲線である。
r2=2a2 cos 2θ
「連珠形」や「ヤコブ・ベルヌーイのレムニスケート」とも呼ばれる。
これはまた、先に述べたように、カッシーニの卵形線において、a=bの場合の曲線である。即ち、直交座標の方程式では、以下のように表される。

(カッシーニの卵形線の特別なケースとして、繰り返しにはなるが)レムニスケートは、x軸とy軸に対して対称な図形で、原点Oで交差する。また、原点Oにおける接線は、y=x とy=-x となる。さらに、原点Oと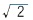 a、-
a、-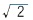 aでx軸と交わる。
aでx軸と交わる。
ループで囲まれた部分の面積は、2つ合わせて、2a2 となる。また、曲線の弧長は楕円積分によって表される。
レムニスケートは、ヤコブとヨハンのベルヌーイ兄弟によって、最初に発見された。曲線は、数字の 8 や(無限大を表す)∞記号に似た形状をしているが、その名前は、ラテン語で「リボンで飾られた」という意味のlemniscatusに由来している。
r2=2a2 cos 2θ
「連珠形」や「ヤコブ・ベルヌーイのレムニスケート」とも呼ばれる。
これはまた、先に述べたように、カッシーニの卵形線において、a=bの場合の曲線である。即ち、直交座標の方程式では、以下のように表される。

(カッシーニの卵形線の特別なケースとして、繰り返しにはなるが)レムニスケートは、x軸とy軸に対して対称な図形で、原点Oで交差する。また、原点Oにおける接線は、y=x とy=-x となる。さらに、原点Oと
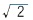 a、-
a、-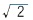 aでx軸と交わる。
aでx軸と交わる。ループで囲まれた部分の面積は、2つ合わせて、2a2 となる。また、曲線の弧長は楕円積分によって表される。
レムニスケートは、ヤコブとヨハンのベルヌーイ兄弟によって、最初に発見された。曲線は、数字の 8 や(無限大を表す)∞記号に似た形状をしているが、その名前は、ラテン語で「リボンで飾られた」という意味のlemniscatusに由来している。
カッシーニの卵形線(レムニスケートを含む)の応用
カッシーニの卵形線は、先に述べたような(幾何学的)特性((1)対称性、(2)2つの焦点からの距離の積が一定、(3)2つの焦点間の距離と別の定数との関係で形状が変化)から、解析幾何学、無線位置特定、産業用途等の分野において、様々なモデル化や解析に利用されている。
例えば、光の反射や屈折の研究において、特定の条件下での光の経路をモデル化するために使用されることがある。これにより、例えば、光の収束や分散を効率的に制御できるような特定の焦点特性を有するレンズやミラーを設計することが可能になる。
また、特定の機械部品の形状の設計や解析において、例えば、特定の強度特性や応力分布を有する部品の設計に役立つことがある。
その他に、特定の放射パターンを有するアンテナの設計や特定の電磁場の分布を解析する際に利用されることがあるようだ。また、バイスタティックレーダー(Bistatic radar)(レーダー波の送信機と受信機を離して設置し両者間を通信で結んだ、主に軍事用のレーダ・システム)では、カッシーニの卵形が、様々なターゲットを検出する仕組みにも使用されているようだ。
例えば、光の反射や屈折の研究において、特定の条件下での光の経路をモデル化するために使用されることがある。これにより、例えば、光の収束や分散を効率的に制御できるような特定の焦点特性を有するレンズやミラーを設計することが可能になる。
また、特定の機械部品の形状の設計や解析において、例えば、特定の強度特性や応力分布を有する部品の設計に役立つことがある。
その他に、特定の放射パターンを有するアンテナの設計や特定の電磁場の分布を解析する際に利用されることがあるようだ。また、バイスタティックレーダー(Bistatic radar)(レーダー波の送信機と受信機を離して設置し両者間を通信で結んだ、主に軍事用のレーダ・システム)では、カッシーニの卵形が、様々なターゲットを検出する仕組みにも使用されているようだ。
デカルトの正葉線
「デカルトの正葉線(folium of Descartes)」は、以下の直交座標の方程式で表される三次曲線である。

その名称は、1638年に、最初にフランスの哲学者かつ数学者であるルネ・デカルト(René Descartes)によって提案され研究されたことに因んでいる。
極座標表示では、以下の通りとなる。

媒介変数表示では、以下の通りとなる。
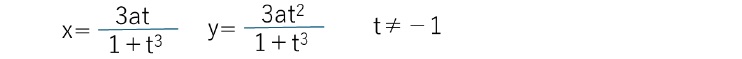
原点Oで自らと交わり、x+y+a=0 を漸近線に有している。
直線y=x とは、原点と(3a/2, 3a/2)の2点で交わる。
曲線は、以下の3つの部分で構成される。
・t<―1 の時 x>0、y<0 の部分の翼
・-1<t<0 の時 x<0、y>0 の部分の翼
・t≧0 の時 x>0、y>0 の部分のループ
なお、ループで囲まれる部分の面積は、S=3a2/2 となる。
さらには、翼部分と漸近線との間の領域の面積も、S=3a2/2 となる。

その名称は、1638年に、最初にフランスの哲学者かつ数学者であるルネ・デカルト(René Descartes)によって提案され研究されたことに因んでいる。
極座標表示では、以下の通りとなる。

媒介変数表示では、以下の通りとなる。
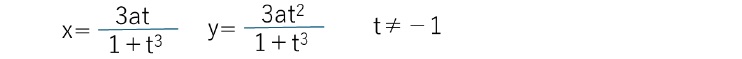
原点Oで自らと交わり、x+y+a=0 を漸近線に有している。
直線y=x とは、原点と(3a/2, 3a/2)の2点で交わる。
曲線は、以下の3つの部分で構成される。
・t<―1 の時 x>0、y<0 の部分の翼
・-1<t<0 の時 x<0、y>0 の部分の翼
・t≧0 の時 x>0、y>0 の部分のループ
なお、ループで囲まれる部分の面積は、S=3a2/2 となる。
さらには、翼部分と漸近線との間の領域の面積も、S=3a2/2 となる。
デカルトの正葉線の応用
デカルトの正葉線は、数学的には非常に興味深い曲線で、数学教育において、微分積分学や解析幾何学の授業で、曲線の性質や方程式の解法を学ぶための例としてよく取り上げられる。
一方で、一般社会において直接的に利用されることは少ないようだ。ただし、その曲線の滑らかさや対称性といった特性から、例えば、コンピュータグラフィックスにおける曲線の描画や形状のモデリングにおいて、利用されている。また、工学分野の流体力学や構造解析において、デカルトの正葉線のような数学的曲線が利用されることもあるようだ。
一方で、一般社会において直接的に利用されることは少ないようだ。ただし、その曲線の滑らかさや対称性といった特性から、例えば、コンピュータグラフィックスにおける曲線の描画や形状のモデリングにおいて、利用されている。また、工学分野の流体力学や構造解析において、デカルトの正葉線のような数学的曲線が利用されることもあるようだ。
最後に
以上、今回は、「カッシーニの卵形線(らんけいせん)」、「レムニスケート」、「デカルトの正葉線」と呼ばれるものについて、報告してきた。
これらの曲線については、一般の方々にとっては、あまり馴染みがないものだと思われる。ただし、そのような曲線も社会の中で使用されて、役に立っている。
次回の曲線シリーズの研究員の眼では、「代数螺旋」や「対数螺旋」といった各種の螺旋について報告する。
これらの曲線については、一般の方々にとっては、あまり馴染みがないものだと思われる。ただし、そのような曲線も社会の中で使用されて、役に立っている。
次回の曲線シリーズの研究員の眼では、「代数螺旋」や「対数螺旋」といった各種の螺旋について報告する。
(2024年11月06日「研究員の眼」)
関連レポート
- 曲線にはどんな種類があって、どう社会に役立っているのか(その1)-円錐曲線(楕円、放物線、双曲線)とは-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その2)-円錐曲線(楕円、放物線、双曲線)が現れる場面-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その3)-カテナリー曲線-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その4)-クロソイド曲線-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その5)-サイクロイド(その性質等)-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その6)-トロコイド・リマソン・カージオイド等-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その7)-サイクロイド・トロコイド(その応用)-
- 曲線にはどんな種類があって、どう社会に役立っているのか(その8)-リサージュ曲線・バラ曲線-
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1) -
2025年10月23日
EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 -
2025年10月23日
中国:25年7~9月期GDPの評価-秋風索莫の気配が漂う中国経済。内需の悪化により成長率は減速 -
2025年10月23日
パワーカップルと小学校受験-データで読み解く暮らしの風景 -
2025年10月22日
高市新政権が発足、円相場の行方を考える~マーケット・カルテ11月号
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【曲線にはどんな種類があって、どう社会に役立っているのか(その9)-カッシーニの卵形線・レムニスケート等-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
曲線にはどんな種類があって、どう社会に役立っているのか(その9)-カッシーニの卵形線・レムニスケート等-のレポート Topへ






















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




