- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 曲線にはどんな種類があって、どう社会に役立っているのか(その4)-クロソイド曲線-
コラム
2024年02月20日
文字サイズ
- 小
- 中
- 大
はじめに
学生時代に、複雑な算式を図表で表すと、いろんな形の曲線が描かれるのを勉強したと思う。この時には、「へー、そうなんだ」ぐらいの認識でおられた方も多く、むしろ、こうした算式の取扱いに四苦八苦して、結果として得られている曲線が、社会において、あるいは自然界において、どのような形で現れていて、どう役立っているのか、については、あまり説明がなく、殆ど勉強する機会もなかったのではないかと思われる。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。前々回までの2回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」について報告した。前回は、「カテナリー曲線」について報告した。
今回は、「クロソイド曲線」について報告する。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。前々回までの2回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」について報告した。前回は、「カテナリー曲線」について報告した。
今回は、「クロソイド曲線」について報告する。
クロソイド曲線とは
「クロソイド曲線(clothoid curve)」というのは、「曲率1が曲線の長さに比例して線形に変化する曲線」である。この曲線が使用されている分野によって、「オイラー螺旋(Euler spiral)」や「コルヌ螺旋(Cornu spiral)」とも呼ばれている。
と説明したものの、殆どの人は、この定義では何が何だかよくわからないというのが本音だろう。
と説明したものの、殆どの人は、この定義では何が何だかよくわからないというのが本音だろう。
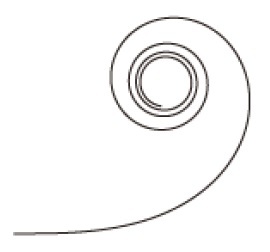 具体的には、クロソイド曲線は、右図のような渦巻きの形状をしている。
具体的には、クロソイド曲線は、右図のような渦巻きの形状をしている。最初はほぼ直線の形状が、曲線に沿って進むほど曲率が大きく(曲率半径が短く)、急な曲線になっていき、螺旋状で(無限に)1点に収束していくような形になる。
身近な例としては、一定の走行速度の下で、車のハンドルを一定の角速度2で回転させたときに、車が走行する軌跡、がクロソイド曲線になっている。
因みに、曲率が常に0の場合に直線となり、曲率が0でない一定値の場合に円になる。
1 曲線の曲がり具合を表す量で、例えば半径 r の円周の曲率は 1/r でrが曲率半径となる。曲率が1次関数で表される場合がクロソイド曲線になる。
2 ある点を回る回転運動の速度を単位時間に進む角度で表したもの
クロソイド曲線の歴史
クロソイド曲線については、複数の分野において、その発見と応用がなされてきたことを反映して、複数の名前が付けられている。このうちの3つの主要なものとして、弾性理論における「オイラー螺旋(Euler spiral)」、光回折のグラフィック計算における「コルヌ螺旋(Cornu spiral)」、鉄道の(直線部分から曲線部分の間の)移行における「鉄道遷移螺旋(railway transition spiral)」が挙げられる。
後にクロソイド曲線として知られる螺旋については、1700年前後から、スイスの数学者であるジェイコブ・ベルヌーイ(Jacob Bernoulli)とその弟のヨハン・ベルヌーイ(Johann Bernoull)、さらにはヨハンの息子のダニエル・ベルヌーイ(Daniel Bernoulli)らのベルヌーイ家の人々によって、問題が提起され、研究されてきた。
ダニエル・ベルヌーイと同時代の親友だったスイスの数学者・物理学者であるレオンハルト・オイラー(Leonhard Euler)は、弾性理論における研究を通じて、1744 年に、現在において「オイラー螺旋」と呼ばれている、螺旋の特性を確立した。
フランスの物理学者であるオーガスチン・フレネル(Augustin Fresnel)は、1818年に光の回折の研究に取り組んで、オイラー螺旋と同じ螺旋を定義する「フレネル積分」を開発した。
1874年、フランスの物理学者であるマリー・アルフレッド・コルヌ(Marie Alfred Cornu)は、光の強度を計算するためのグラフィカルデバイスを考案し、これが彼に因んで「コルヌ螺旋」と名付けられた。
また、イタリアの数学者であるアーネスト・チェザロ(Ernesto Cesaro)は、1886年に、ギリシャ神話で運命を決める3人の女神の1人で、運命の糸を紡ぐ女神であるクロソ(Clotho)に因んで、この螺旋を「クロソイド」と名付けた。この名前は、スピンドル(紡錘)の周りに無限に巻き付く毛糸を連想させるものとなっている。
さらに、1800年代には、遠心加速度の変化による横方向の衝撃を最小限に抑えるために、多くの鉄道技術者が線路の形状を緩やかに湾曲させる方式を模索していたが、 1880年までに、米国の土木技師であるアーサー・ニューウェル・タルボット(Arthur Newell Talbot)が解決策を導き出し、これが「タルボットの螺旋」とも呼ばれる「鉄道遷移螺旋」になっている。
後にクロソイド曲線として知られる螺旋については、1700年前後から、スイスの数学者であるジェイコブ・ベルヌーイ(Jacob Bernoulli)とその弟のヨハン・ベルヌーイ(Johann Bernoull)、さらにはヨハンの息子のダニエル・ベルヌーイ(Daniel Bernoulli)らのベルヌーイ家の人々によって、問題が提起され、研究されてきた。
ダニエル・ベルヌーイと同時代の親友だったスイスの数学者・物理学者であるレオンハルト・オイラー(Leonhard Euler)は、弾性理論における研究を通じて、1744 年に、現在において「オイラー螺旋」と呼ばれている、螺旋の特性を確立した。
フランスの物理学者であるオーガスチン・フレネル(Augustin Fresnel)は、1818年に光の回折の研究に取り組んで、オイラー螺旋と同じ螺旋を定義する「フレネル積分」を開発した。
1874年、フランスの物理学者であるマリー・アルフレッド・コルヌ(Marie Alfred Cornu)は、光の強度を計算するためのグラフィカルデバイスを考案し、これが彼に因んで「コルヌ螺旋」と名付けられた。
また、イタリアの数学者であるアーネスト・チェザロ(Ernesto Cesaro)は、1886年に、ギリシャ神話で運命を決める3人の女神の1人で、運命の糸を紡ぐ女神であるクロソ(Clotho)に因んで、この螺旋を「クロソイド」と名付けた。この名前は、スピンドル(紡錘)の周りに無限に巻き付く毛糸を連想させるものとなっている。
さらに、1800年代には、遠心加速度の変化による横方向の衝撃を最小限に抑えるために、多くの鉄道技術者が線路の形状を緩やかに湾曲させる方式を模索していたが、 1880年までに、米国の土木技師であるアーサー・ニューウェル・タルボット(Arthur Newell Talbot)が解決策を導き出し、これが「タルボットの螺旋」とも呼ばれる「鉄道遷移螺旋」になっている。
クロソイド曲線の基本式
クロソイド曲線の応用-道路のカーブ-
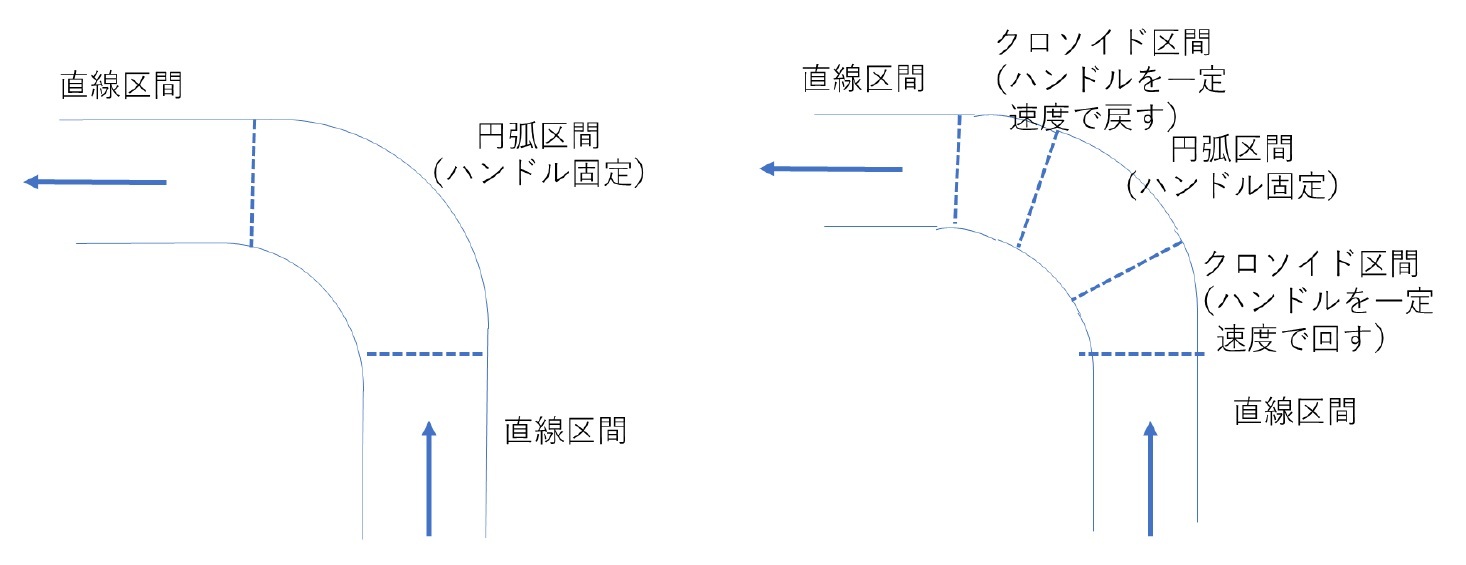
この時もし、カーブが円弧になっていたとすると、円弧区間に入った瞬間に円弧のカーブに対応する形でハンドルを一気に切らなければいけなくなる。また円弧区間から直線区間に戻った瞬間に今度は一気にハンドルを元に戻さなければならなくなる。このハンドル操作はかなり危険で運転者に負担のかかるものになる3。
一方で、もし直線区間から円弧区間に入る前や円弧区間から直線区間に戻る前に、クロソイド区間があれば、この区間ではハンドルを一定速度で回したり、戻したりすることができる(円弧区間ではハンドルは固定していればよい)ことになり、ハンドル操作がかなり安定的なものとなり、運転者の負担も軽いものとなる。
このように、クロソイド曲線の利用は、車の安全運転のために欠かせないものとなっている。
クロソイド曲線は、このように直線部分と円弧部分をつなぐ「緩和曲線」4の一種となっている。
因みに、世界で最初に高速道路にクロソイド曲線を取り入れたのは、ドイツのアウトバーンだと言われている。また、日本で最初に道路設計に導入された場所は国道17号線三国峠だと言われている。
以下のジャンクションの写真は、クロソイド曲線が見られる実際例となっている。
一方で、もし直線区間から円弧区間に入る前や円弧区間から直線区間に戻る前に、クロソイド区間があれば、この区間ではハンドルを一定速度で回したり、戻したりすることができる(円弧区間ではハンドルは固定していればよい)ことになり、ハンドル操作がかなり安定的なものとなり、運転者の負担も軽いものとなる。
このように、クロソイド曲線の利用は、車の安全運転のために欠かせないものとなっている。
クロソイド曲線は、このように直線部分と円弧部分をつなぐ「緩和曲線」4の一種となっている。
因みに、世界で最初に高速道路にクロソイド曲線を取り入れたのは、ドイツのアウトバーンだと言われている。また、日本で最初に道路設計に導入された場所は国道17号線三国峠だと言われている。
以下のジャンクションの写真は、クロソイド曲線が見られる実際例となっている。
3 速度が一定の円運動においては、向心力や遠心力は曲率に比例する。直線区間から円弧区間に入ることで、曲率が不連続に変化する場合、遠心力が急激にかかることになり、車に乗っている人にも負担がかかることになる。
4 曲率0の直線から円曲線へ曲率を変化させる線が「緩和曲線」となる。例えば、鉄道の場合、鉄道車両が直線路から急に曲線路に進入したり、曲線路から別の曲線路に進入したりするときの激しいショックを避けるために設ける特別の線路の曲線となり、「遷移曲線(transition curve)」ともいう。緩和曲線には、クロソイド曲線に加えて、後述の三次放物線やサイン半波長逓減曲線等がある。
(2024年02月20日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる -
2025年10月24日
企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年10月24日
消費者物価(全国25年9月)-コアCPI上昇率は拡大したが、先行きは鈍化へ -
2025年10月24日
保険業界が注目する“やせ薬”?-GLP-1は死亡率改善効果をもたらすのか -
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1)
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【曲線にはどんな種類があって、どう社会に役立っているのか(その4)-クロソイド曲線-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
曲線にはどんな種類があって、どう社会に役立っているのか(その4)-クロソイド曲線-のレポート Topへ


















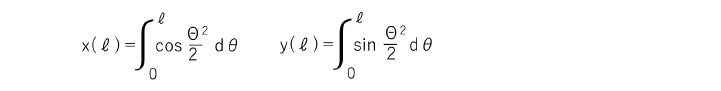


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




