- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 分数について(その2)-連分数に関する話題-
コラム
2023年04月18日
文字サイズ
- 小
- 中
- 大
はじめに
分数という概念は、小数の概念とは異なり、古代エジプトの時代から使用されていた。ただし、その使用のされ方は、現在とは必ずしも同様なものにはなっていない。
今回は、分数を巡る話題について、5回に分けて報告することにしているが、前回はその定義、起源、表記法等について述べた。今回は、連分数に関する話題について、述べることとする。
今回は、分数を巡る話題について、5回に分けて報告することにしているが、前回はその定義、起源、表記法等について述べた。今回は、連分数に関する話題について、述べることとする。
ここで、「・・・」が有理数の場合には、ある自然数nにおいて分母がanという整数のみとなって、展開が有限で終了して、「有限連分数」となる。一方で、「・・・」が無理数の場合には、このような展開が無限に行われて、「無限連分数」となる。
数字の連分数表示
有理数は有限正則連分数で表すことができ、その逆もまた真で、有限正則連分数で表すことができる数は有理数となる。このように有理数と有限連分数は本質的に1対1に対応している。
また、任意の無理数は無限正則連分数として一意に表される。このうち、「2次無理数(quadratic irrational)」(整数係数二次方程式の根である無理数)の正則連分数展開は、必ず循環し、これを「循環連分数」、循環する部分を「循環節」という。逆に、正則連分数展開が循環連分数となる数は2次無理数となる。これは、18世紀のフランスの大数学者であるジョゼフ=ルイ・ラグランジュ(Joseph-Louis Lagrange )によって証明されている1。
と、ここまでの説明を聞くと、小数に関する研究員の眼「小数について(その2)-循環小数を巡る話題-」(2023.1.30)において紹介してきた循環小数や循環節との類似性を意識される方もいらっしゃるのではないかと思われる。これらの関係は以下のようになっている。
また、任意の無理数は無限正則連分数として一意に表される。このうち、「2次無理数(quadratic irrational)」(整数係数二次方程式の根である無理数)の正則連分数展開は、必ず循環し、これを「循環連分数」、循環する部分を「循環節」という。逆に、正則連分数展開が循環連分数となる数は2次無理数となる。これは、18世紀のフランスの大数学者であるジョゼフ=ルイ・ラグランジュ(Joseph-Louis Lagrange )によって証明されている1。
と、ここまでの説明を聞くと、小数に関する研究員の眼「小数について(その2)-循環小数を巡る話題-」(2023.1.30)において紹介してきた循環小数や循環節との類似性を意識される方もいらっしゃるのではないかと思われる。これらの関係は以下のようになっている。
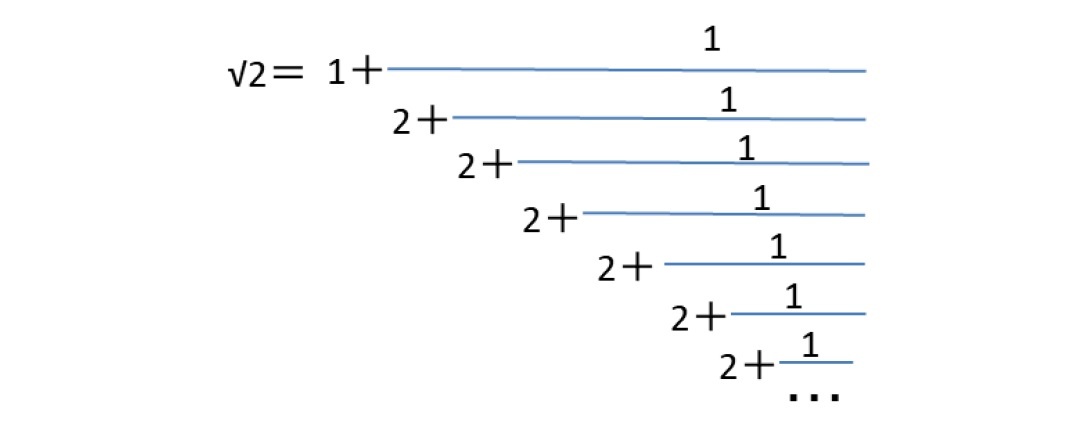
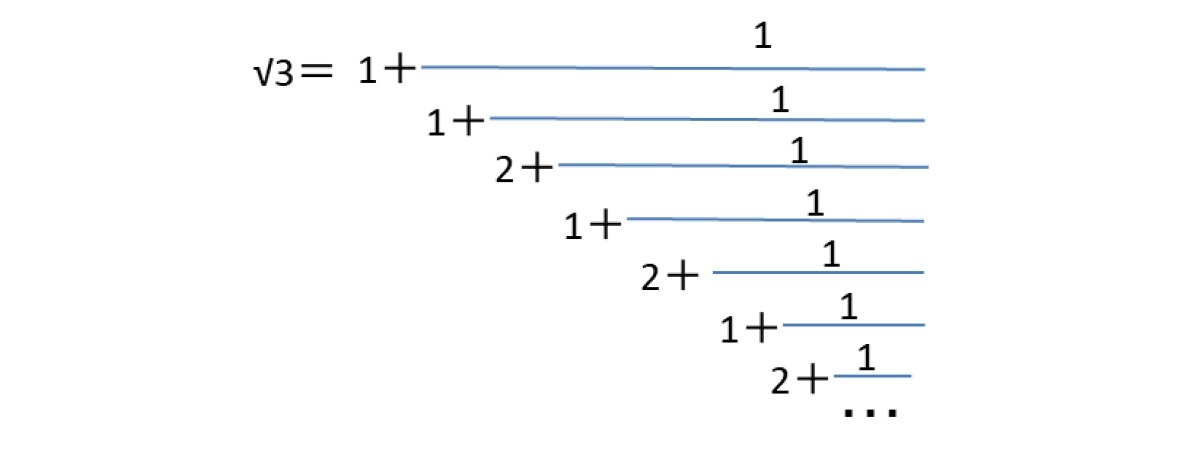
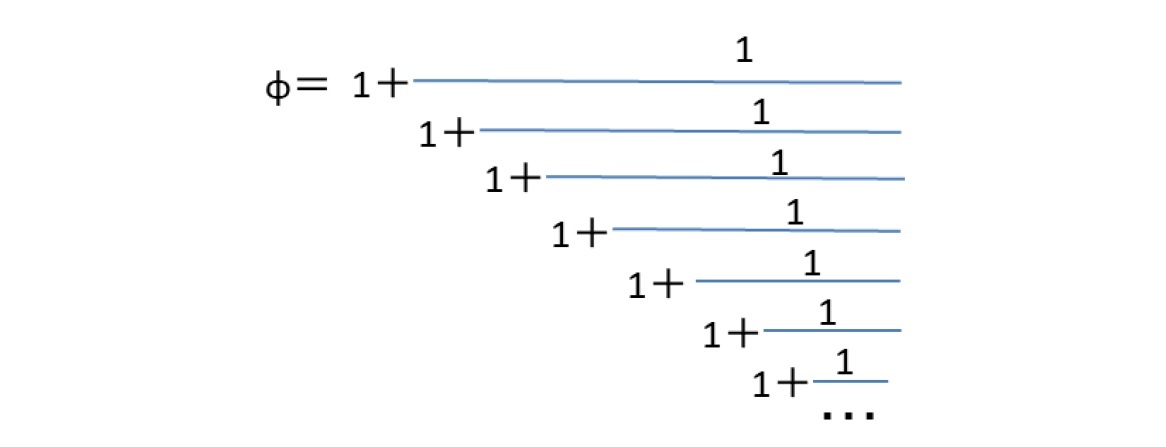
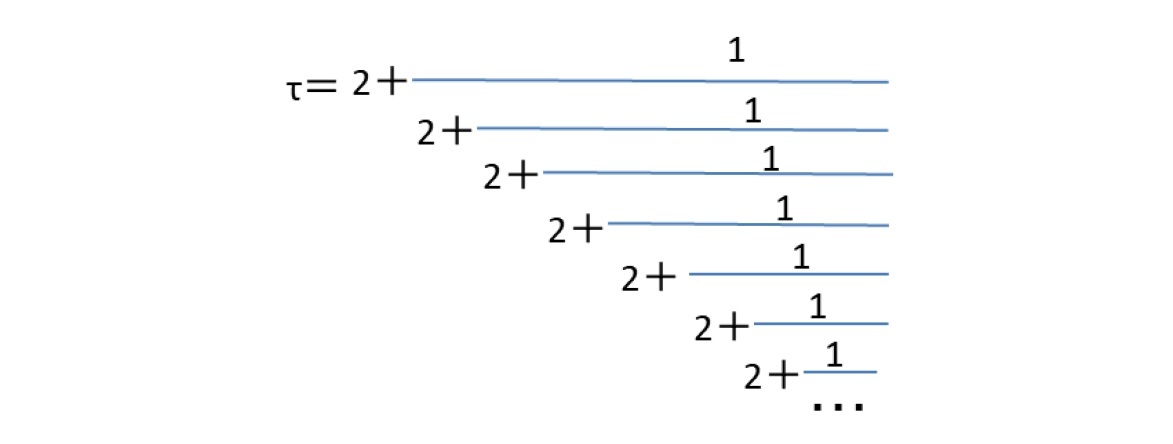
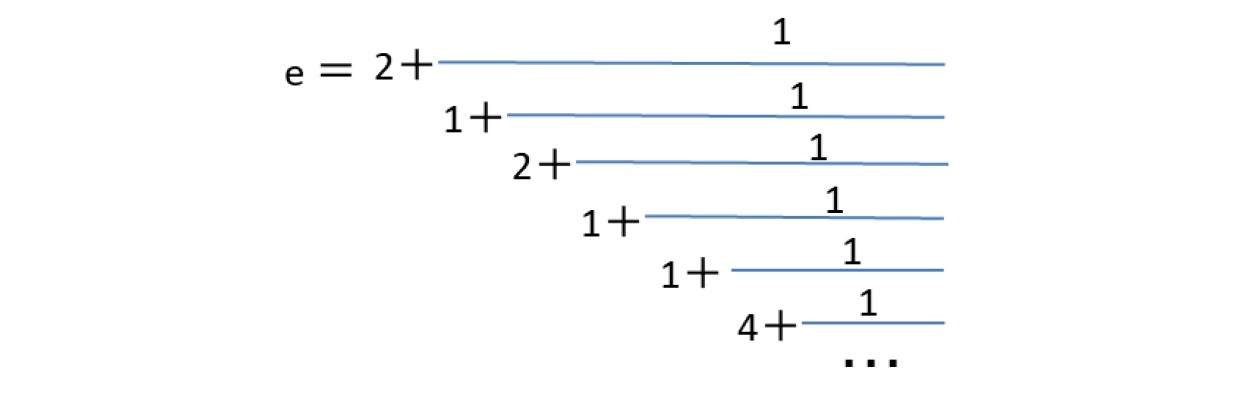
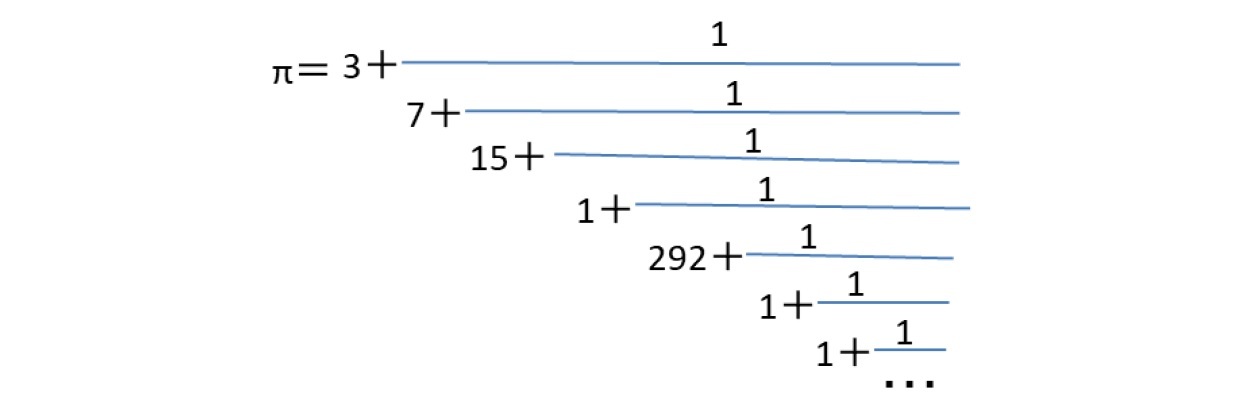
従って、以前にも述べたように、また下記で示すように、√2、√3 黄金数φ(=(1+√5)/2)、白銀数τ(=1+√2)は、2次無理数で、循環連分数に展開されるが、ネイピア数eや円周率πは非循環連分数に展開されることになる。
1 なお、このあたりの無理数に関する話題については、研究員の眼「無理数について(その2)-無理数の(有理数や無理数)べき乗や無理数度等-」(2021.12.13)でも紹介した。
1 なお、このあたりの無理数に関する話題については、研究員の眼「無理数について(その2)-無理数の(有理数や無理数)べき乗や無理数度等-」(2021.12.13)でも紹介した。
連分数による実数の近似
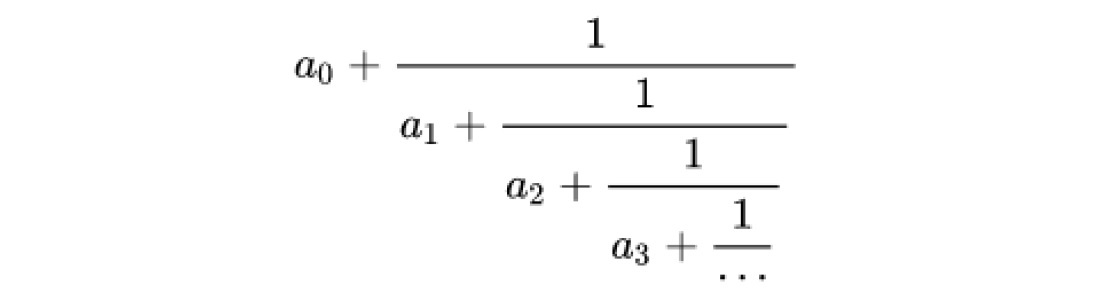
実数αを連分数展開したものを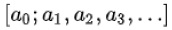 とする時、
とする時、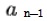 までで打ち切った連分数を実数αの「n番目の近似分数」という。
までで打ち切った連分数を実数αの「n番目の近似分数」という。
有理数p/q(pとqは互いに素)の連分数展開において、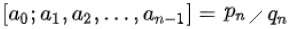 (
(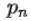 と
と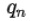 は互いに素な自然数)とするとき、
は互いに素な自然数)とするとき、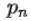 /
/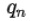 がn番目の近似分数となる。
がn番目の近似分数となる。
この時、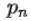 /
/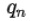 は、nが大きくなるにつれて、p/qとの差の符号を交互に変更させながら、p/qに近づいていく。即ち、
は、nが大きくなるにつれて、p/qとの差の符号を交互に変更させながら、p/qに近づいていく。即ち、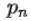 /
/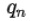 は、p/qの前後で振動しながらp/qに近づいていく。
は、p/qの前後で振動しながらp/qに近づいていく。
無理数αに関して、任意の有理数p/q(0<q<Q)(≠P/Q)に対して、
|α-p/q|>|α-P/Q|
を満たす有理数P/Qをαの「最良近似分数」というが、連分数展開で得られる近似分数は最良近似分数となる。
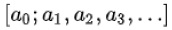 とする時、
とする時、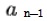 までで打ち切った連分数を実数αの「n番目の近似分数」という。
までで打ち切った連分数を実数αの「n番目の近似分数」という。有理数p/q(pとqは互いに素)の連分数展開において、
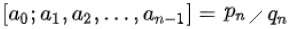 (
(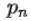 と
と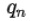 は互いに素な自然数)とするとき、
は互いに素な自然数)とするとき、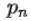 /
/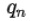 がn番目の近似分数となる。
がn番目の近似分数となる。この時、
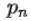 /
/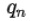 は、nが大きくなるにつれて、p/qとの差の符号を交互に変更させながら、p/qに近づいていく。即ち、
は、nが大きくなるにつれて、p/qとの差の符号を交互に変更させながら、p/qに近づいていく。即ち、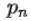 /
/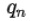 は、p/qの前後で振動しながらp/qに近づいていく。
は、p/qの前後で振動しながらp/qに近づいていく。無理数αに関して、任意の有理数p/q(0<q<Q)(≠P/Q)に対して、
|α-p/q|>|α-P/Q|
を満たす有理数P/Qをαの「最良近似分数」というが、連分数展開で得られる近似分数は最良近似分数となる。
このような連分数展開を通じて、πの近似値を分数で表し、算出することができることになる。
(2023年04月18日「研究員の眼」)
関連レポート
- 分数について(その1)-分数の起源等はどうなっているのか-
- 無理数について(その2)-無理数の(有理数や無理数)べき乗や無理数度等-
- 小数について(その2)-循環小数を巡る話題-
- フィボナッチ数列について(その1)-フィボナッチ数列とはどのようなものでどんな性質を有しているのか-
- 図形数について(その1)-2次元平面図形に関する図形数-
- 小数について(その3)-非循環小数を巡る話題-
- 黄金比φについて(その1)-黄金比とはどのようなものなのか-
- 白銀比τ等について-白銀比とはどのようなもので、どんな場面で使用されているのか-
- ネイピア数eについて-ネイピア数とは何か、ネイピア数はどんな意味を有しているのか-
- 円周率πが現われる世界-ビュフォンの針の問題-
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【分数について(その2)-連分数に関する話題-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
分数について(その2)-連分数に関する話題-のレポート Topへ


















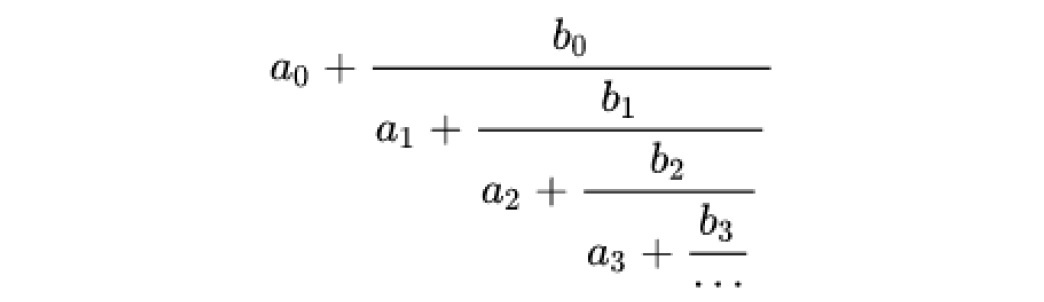
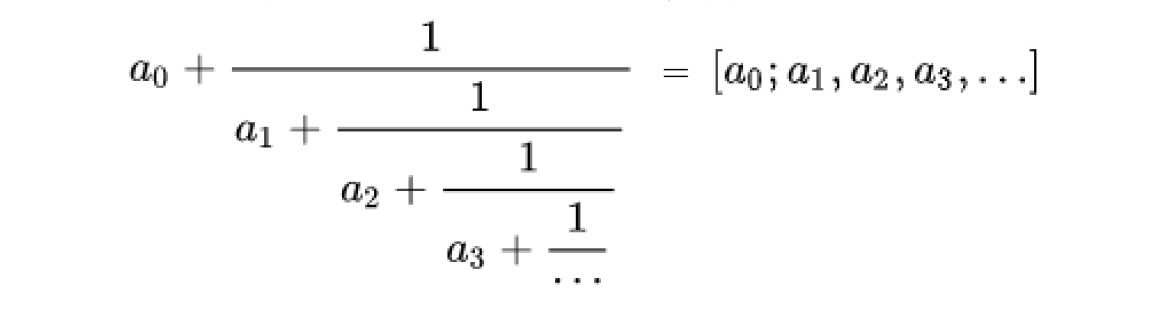

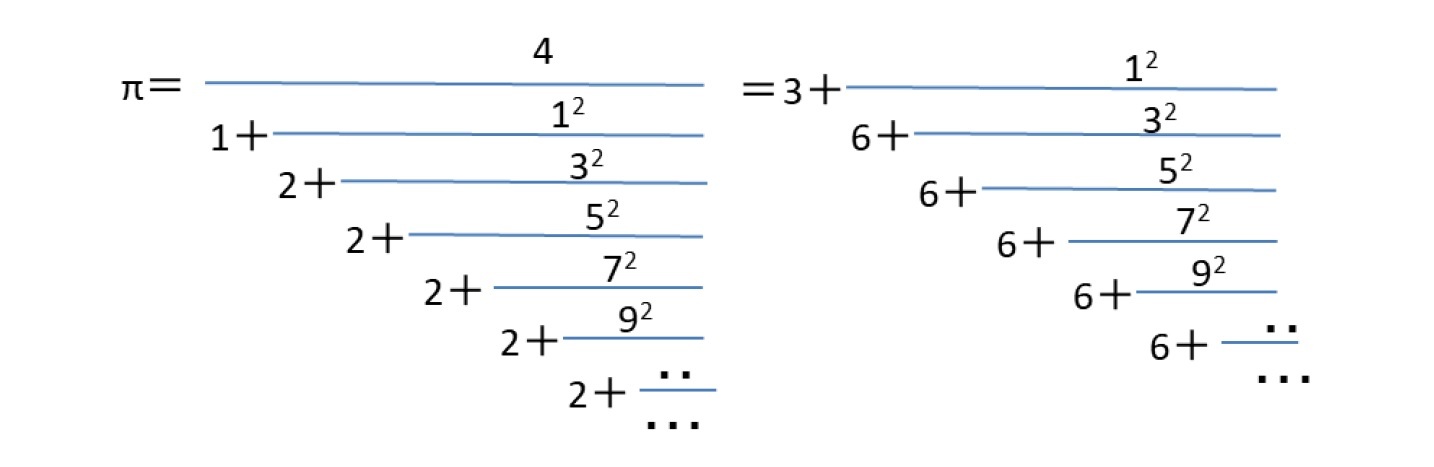

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




